(Just found I can post here – I hope it is not a mistake. This is a slightly shortened version of a piece which I have published on my blog. I am sorry it is so long but I struggle to make it any shorter. I am grateful for any comments. I will look at UD for comments as well – but not sure where they would appear.).
I have been rereading Bernoulli’s Principle of Insufficient Reason and Conservation of Information in Computer Search by William Dembski and Robert Marks. It is an important paper for the Intelligent Design movement as Dembski and Marks make liberal use of Bernouilli’s Principle of Insufficient Reason (BPoIR) in their papers on the Law of Conservation of Information (LCI). For Dembski and Marks BPoIR provides a way of determining the probability of an outcome given no prior knowledge. This is vital to the case for the LCI.
The point of Dembski and Marks paper is to address some fundamental criticisms of BPoIR. For example J M Keynes (along with with many others) pointed out that the BPoIR does not give a unique result. A well-known example is applying BPoIR to the specific volume of a given substance. If we know nothing about the specific volume then someone could argue using BPoIR that all specific volumes are equally likely. But equally someone could argue using BPoIR all specific densities are equally likely. However, as one is the reciprocal of the other, these two assumptions are incompatible. This is an example based on continuous measurements and Dembski and Marks refer to it in the paper. However, having referred to it, they do not address it. Instead they concentrate on the examples of discrete measurements where they offer a sort of response to Keynes’ objections. What they attempt to prove is a rather limited point about discrete cases such as a pack of cards or protein of a given length. It is hard to write their claim concisely – but I will give it a try.
Imagine you have a search space such as a normal pack of cards and a target such as finding a card which is a spade. Then it is possible to argue by BpoIR that, because all cards are equal, the probability of finding the target with one draw is 0.25. Dembski and Marks attempt to prove that in cases like this that if you decide to do a “some to many” mapping from this search space into another space then you have at best a 50% chance of creating a new search space where BPoIR gives a higher probability of finding a spade. A “some to many” mapping means some different way of viewing the pack of cards so that it is not necessary that all of them are considered and some of them may be considered more often than others. For example, you might take a handful out of the pack at random and then duplicate some of that handful a few times – and then select from what you have created.
There are two problems with this.
1) It does not address Keynes’ objection to BPoIR
2) The proof itself depends on an unjustified use of BPoIR.
But before that a comment on the concept of no prior knowledge.
The Concept of No Prior Knowledge
Dembski and Marks’ case is that BPoIR gives the probability of an outcome when we have no prior knowledge. They stress that this means no prior knowledge of any kind and that it is “easy to take for granted things we have no right to take for granted”. However, there are deep problems associated with this concept. The act of defining a search space and a target implies prior knowledge. Consider finding a spade in pack of cards. To apply BPoIR at minimum you need to know that a card can be one of four suits, that 25% of the cards have a suit of spades, and that the suit does not affect the chances of that card being selected. The last point is particularly important. BPoIR provides a rationale for claiming that the probability of two or more events are the same. But the events must differ in some respects (even if it is only a difference in when or where they happen) or they would be the same event. To apply BPoIR we have to know (or assume) that these differences are not relevant to the probability of the events happening. We must somehow judge that the suit of the card, the head or tails symbols on the coin, or the choice of DNA base pair is irrelevant to the chances of that card, coin toss or base pair being selected. This is prior knowledge.
In addition the more we try to dispense with assumptions and knowledge about an event then the more difficult it becomes to decide how to apply BPoIR. Another of Keynes’ examples is a bag of 100 black and white balls in an unknown ratio of black to white. Do we assume that all ratios of black to white are equally likely or do we assume that each individual ball is equally likely to be black or white? Either assumption is equally justified by BPoIR but they are incompatible. One results in a uniform probability distribution for the number of white balls from zero to 100; the other results in a binomial distribution which greatly favours roughly equal numbers of black and while balls.
Looking at the problems with the proof in Dembski and Marks’ paper.
The Proof does not Address Keynes’ objection to BPoIR
Even if the proof were valid then it does nothing to show that the assumption of BPoIR is correct. All it would show (if correct) was that if you do not use BPoIR then you have 50% or less chance of improving your chances of finding the target. The fact remains that there are many other assumptions you could make and some of them greatly increase your chances of finding the target. There is nothing in the proof that in anyway justifies assuming BPoIR or giving it any kind of privileged position.
But the problem is even deeper. Keynes’ point was not that there are alternatives to using BPoIR – that’s obvious. His point was that there are different incompatible ways of applying BPoIR. For example, just as with the example of black and white balls above, we might use BPoIR to deduce that all ratios of base pairs in a string of DNA are equally likely. Dembski and Marks do not address this at all. They point out the trap of taking things for granted but fall foul of it themselves.
The Proof Relies on an Unjustified Use of BPoIR
The proof is found in appendix A of the paper and this is the vital line:
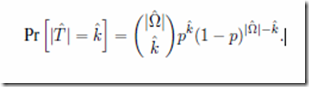
This is the probability that a new search space created from an old one will include k members which were part of the target in the original search space. The equation holds true if the new search space is created by selecting elements from old search space at random; for example, by picking a random number of cards at random from a pack. It uses BPoIR to justify the assumption that each unique way of picking cards is equally likely. This can be made clearer with an example.
Suppose the original search space comprises just the four DNA bases, one of which is the target. Call them x, y, z and t. Using BPoIR, Dembski and Marks would argue that all of them are equally likely and therefore the probability of finding t with a single search is 0.25. They then consider all the possible ways you might take a subset of that search space. This comprises:
Subsets with
no items
just one item: x,y,z and t
with two items: xy, xz, yz, tx, ty, tz
with three items: xyz, xyt, xzt, yzt
with four items: xyzt
A total of 16 subsets.
Their point is that if you assume each of these subsets is equally likely (so the probability of one of them being selected is 1/16) then 50% of them have a probability of finding t which is greater than or equal to probability in the original search space (i.e. 0.25). To be specific new search spaces where probability of finding t is greater than 0.25 are t, tx, ty, tz, xyt, xzt, yzt and xyzt. That is 8 out of 16 which is 50%.
But what is the justification for assuming each of these subsets are equally likely? Well it requires using BPoIR which the proof is meant to defend. And even if you grant the use of BPoIR Keynes’ concerns apply. There is more than one way to apply BPoIR and not all of them support Dembski and Marks’ proof. Suppose for example the subset was created by the following procedure:
- Start with one member selected at random as the subset
- Toss a dice,
- If it is two or less then stop and use current set as subset
- If it is a higher than two then add another member selected at random to the subset
- Continue tossing until dice throw is two or less or all four members in are in subset
This gives a completely different probability distribution.
The probability of:
single item subset (x,y,z, or t) = 0.33/4 = 0.083
double item subset (xy, xz, yz, tx, ty, or tz) = 0.66*0.33/6 = 0.037
triple item subset (xyz, xyt, xzt, or yzt) = 0.66*0.33*0.33/4 = 0.037
four item subset (xyzt) = 0.296
So the combined probability of the subsets where probability of selecting t is ≥ 0.25 (t, tx, ty, tz, xyt, xzt, yzt, xyzt) = 0.083+3*(0.037)+3*(0.037)+0.296 = 0.60 (to 2 dec places) which is bigger than 0.5 as calculated using Dembski and Marks assumptions. In fact using this method, the probability of getting a subset where the probability of selecting t ≥ 0.25 can be made as close to 1 as desired by increasing the probability of adding a member. All of these methods treat all four members of the set equally and are equally justified under BpoIR as Dembski and Marks assumption.
Conclusion
Dembski and Marks paper places great stress on BPoIR being the way to calculate probabilities when there is no prior knowledge. But their proof itself includes prior knowledge. It is doubtful whether it makes sense to eliminate all prior knowledge, but if you attempt to eliminate as much prior knowledge as possible, as Keynes does, then BPoIR proves to be an illusion. It does not give a unique result and some of the results are incompatible with their proof.
, and the evidence of complex life as 
. What we want to know is the posterior probability that 
is true, given ![\[P(H_{G}|L_N)}\]](http://theskepticalzone.com/wp/wp-content/ql-cache/quicklatex.com-3f2ddf730ccbd821f6f5020f49419cdb_l3.png "Rendered by QuickLaTeX.com")
