Lizzie Allan Miller said:
Here’s a simple experiment one can actually try. Take a bag of M&M’s, and without peeking reach in and grab one. Eat it. Then grab another and return it to the bag with another one, from a separate bag, of the same colour. Give it a shake. I guarantee (and if you tell me how big your bag is I’ll have a bet on how long it’ll take) that your bag will end up containing only one colour. Every time. I can’t tell you which colour it will be, but fixation will happen.
I’ve written an interactive browser based version you can explore this idea with.
http://mandmcounter.appspot.com/emeniem.html
You can change the bag size, number of colors, speed of each round and graph the results, as well as see in real time the number of each color that remains and watch the end-game in detail.
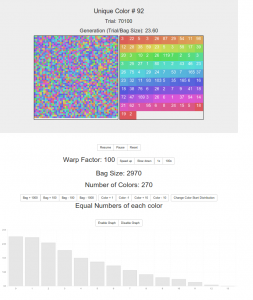
You start with a bag size of 1950, containing 150 colors. Click reset to rerun the simulation with the same parameters, or change them and it automatically restarts with the new parameters.
You’ll probably need a relatively up to date browser.
Some explanations, from top to bottom. But just go press the buttons, that’ll make more sense 🙂
Unique Color # is the number of colors that remain in the bag. This updates in real time.
The trial number is how many times we’ve reached into the bag, ate one, picked one and replaced two.
The generation is the number of trials divided by the bag size. Fairly arbitrary.
The two squares show, on the left, a representation of the bag. Items are removed and inserted at random places. On the right are the colors in the bag and superimposed on them are the numbers of those colors in the bag.
You can resume, pause and reset the simulation. Reset uses the current values and generates a new random bag.
Warp factor is how many trials are run between each update of the screen. The default is one, so “real time”. Increase and decrease that with the buttons as you like.
Bag size is the bag size you ended up with after some constraints relating to number of colors were satisfied (if you want equal numbers of colors the bag size has to be a multiple of that). There may be some faulty logic here!
The number of colors is, well, the number of colors you’ve set to be in the bag. It’s actually the range of possible colors that the bag can choose from so sometimes you might end up with fewer in the bag at the start of a round then you set in the “unequal number of colors mode”. But bigger bags will of course usually use up all possible colors. And equal color mode (the default) always starts with all colors in the bag.
You can change the size of the bag, subject to some lower limits (e.g. the number of colors) and the number of colors can also be changed, up to 350 currently.
Clicking “change color start distribution” sets either equal numbers of colors at the start of the round (so no one color will obviously ‘win’ due to a starting advantage) and random numbers of each color at the start. The default is to have equal numbers.
You may find some weirdness with very large bag sizes.
Finally the graph shows a count of colors over time, if you change the warp factor the timing of the graph does not update accordingly however (I had to finish this up!). So change the warp speed then click reset and the graph will be ok for that round.
I’ll add a “add a single black one” button in the next couple of days, but in the meanwhile just pick a color and root for that!
So I hope this is useful/interesting/whatever, and if you have feature requests, bugs, questions or ideas for further such toys please feel free to note them as a comment in this thread.
Please keep comments regarding the original discussion etc to the relevant threads, not this one.

Joe Felsenstein,
According to a diffusion approximation in Otto & Day 2007 (A Biologist’s Guide to Mathematical Modelling in Ecology and Evolution, p. 681), for haploids the mean time to fixation, given initial frequency p0, is given by
mean(t_fix) = -2N (1-p0)/p0 ln(1-p0) generations
For p0=1/N, i.e. for a single mutant, that can be approximated as
mean(t_fix) = 2N-1+O(1/N^2)
or even more accurately for smallish N
mean(t_fix) = 2N-1-1/(3N)-1/(6N^2)+O(1/N^4)
For diploids, multiply by 2.
Welcome IdoP
The melanic mutation was not a neutral mutation, therefore it is not relevant to the model of neutral drift that we are discussing.
But to answer your question, you are confusing the model with the territory. the population of peppered moths is not fixed. In addition, the environment in which the peppered moth lives has changed significantly, from favoring light-colored moths before the early 19th century to favoring dark-colored moths from the early 19th century to the mid 20th century and changed again to favor light-colored moths from the mid 20th century until now.
I understand your question to be “where did the melanic form come from in the 1800s, if the light-peppered form had been so well -adapted before that time?” — and especially considering that,one or the other trait “should” have fixed in the population over time (as demonstrated in the random evolution model threads), it is a good question.
As usual I’m going to be lazy and not dig for specific journal papers on peppered-moth genetics and go with general knowledge of genetics. In general, skin color/fur color/stripes/patches are controlled by a few genes, and there are uncountable ways those genes can break with a single point mutation. A single mutation can result in no color where there was color in the parent variety, or can result in a reversion to the ancestral plain color by breaking the development of stripes/speckles. Since I haven’t done the research, I don’t know if that’s true of peppered moths, but it’s a reasonable basic assumption.
So I think we have no worries about the speckled variety having been previously fixed; if it had been fixed, any random mutation to the wing-color gene could have resulted in a black version. If mutations happened occasionally in the pre-pollution forest, then those black ones had much less chance of surviving to reproduce their mutation, but the first time a black-mutation occurred in the polluted-forest range, then that is when the black ones finally had greater chance of surviving in the face of bird predation.
Of course, if a black mutation was not already present, nor did one fortunately occur during the polluted-forest timespan, the whole species may have gone extinct in the extreme case of bird predation reducing the peppered population to a few remnants that could not mate up in sufficient numbers. Extinction happens. Most species don’t happen to get the mutations they “need” to survive a changing environment.
But it doesn’t surprise us when one species, say, the peppered moth, does get the mutation they “need” to survive. We expect “good luck” to happen at least some times to some of the millions of species we currently share the planer with.
Previously posted news: The peppered moth’s dark genetic past revealed. The full paper is open access with free registration at Industrial Melanism in British Peppered Moths Has a Singular and Recent Mutational Origin.
Oh, thanks for that.
This is Pólya’s urn. http://en.wikipedia.org/wiki/Polya_urn_model
Tom English,
Although the Wiki does not mention evolutionary theory as an application.
http://arxiv.org/pdf/math/0407129.pdf
Now it does, just added to “Polya urn model” in the list of variants of that model.
Strangely, the paper on generalized urn models in Arxiv does not directly mention the Moran model, which is a widely-used model in population genetics.