My problem with the IDists’ 500 coins question (if you saw 500 coins lying heads up, would you reject the hypothesis that they were fair coins, and had been fairly tossed?) is not that there is anything wrong with concluding that they were not. Indeed, faced with just 50 coins lying heads up, I’d reject that hypothesis with a great deal of confidence.
It’s the inference from that answer of mine is that if, as a “Darwinist” I am prepared to accept that a pattern can be indicative of something other than “chance” (exemplified by a fairly tossed fair coin) then I must logically also sign on to the idea that an Intelligent Agent (as the alternative to “Chance”) must inferrable from such a pattern.
This, I suggest, is profoundly fallacious.
First of all, it assumes that “Chance” is the “null hypothesis” here. It isn’t. Sure, the null hypothesis (fair coins, fairly tossed) is rejected, and, sure, the hypothesized process (fair coins, fairly tossed) is a stochastic process – in other words, the result of any one toss is unknowable before hand (by definition, otherwise it wouldn’t be “fair”), and both the outcome sequence of 500 tosses and the proportion of heads in the outcome sequence is also unknown. What we do know, however, because of the properties of the fair-coin-fairly-tossed process, is the probability distribution, not only of the proportions of heads that the outcome sequence will have, but also of the distribution of runs-of-heads (or tails, but to keep things simple, I’ll stick with heads).
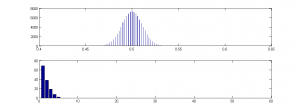
And in fact, I simulated a series of 100,000 such runs (I didn’t go up to the canonical 2^500 runs, for obvious reasons), using MatLab, and here is the outcome:
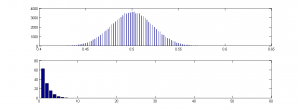 As you can see from the top plot, the distribution is a beautiful bell curve, and in none of the 100,000 runs do I get anything near even as low as 40% Heads or higher than 60% Heads.
As you can see from the top plot, the distribution is a beautiful bell curve, and in none of the 100,000 runs do I get anything near even as low as 40% Heads or higher than 60% Heads.
Moreover, I also plotted the average length of runs-of-heads – the average is just over 2.5, and the maximum is less than 10, and the frequency distribution is a lovely descending curve (lower plot).
If therefore, I were to be shown a sequence of 500 Heads and Tails, in which the proportion of Heads was:
- less than, say 40%, OR
- greater than, say 60%, OR
- the average length runs-of-heads was a lot more than 2.5, OR
- the distribution of the proportions was not a nice bell curve, OR
- the distribution of the lengths of runs-of-heads was not a nice descending Poisson like the one in lower plot,
I would also reject the null hypothesis that the process that generated the sequence was “fair coins, fairly tossed”. For example:
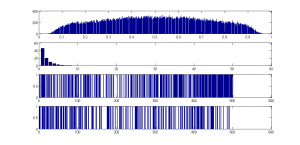
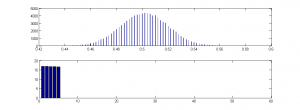 This was another simulation. As you can see, the bell curve is pretty well identical to the first, and the proportions of heads are just as we’d expect from fair coins, fairly tossed – but can we conclude it was the result of “fair coins, fairly tossed”? Well, no. Because look at the lower plot – the mean length of runs of heads is 2.5, as before, but the distribution is very odd. There are no runs of heads longer than 5, and all lengths are of pretty well equal frequency. Here is one of these runs, where 1 stands for Heads and 0 stands for tails:
This was another simulation. As you can see, the bell curve is pretty well identical to the first, and the proportions of heads are just as we’d expect from fair coins, fairly tossed – but can we conclude it was the result of “fair coins, fairly tossed”? Well, no. Because look at the lower plot – the mean length of runs of heads is 2.5, as before, but the distribution is very odd. There are no runs of heads longer than 5, and all lengths are of pretty well equal frequency. Here is one of these runs, where 1 stands for Heads and 0 stands for tails:
1 0 1 1 1 0 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 1 1 1 0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0 0 1 0 0 0 0 0 1 1 1 1 1 0 1 1 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 1 0 1 1 1 1 1 0 0 0 0 1 0 1 1 0 0 0 0 0 1 1 0 0 0 0 1 1 1 1 1 0 0 1 1 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 0 1 1 1 1 1 0 1 1 0 0 0 1 1 1 1 0 1 1 1 1 1 0 0 0 0 0 1 0 1 0 0 1 1 1 1 0 1 1 1 1 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 1 0 1 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 1 1 1 0 0 0 0 1 1 1 1 0 1 1 1 1 1 0 0 0 0 0 1 1 1 0 0 0 0 1 1 0 0 0 0 1 1 0 1 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 1 1 1 1 1 0 1 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 0 1 0 0 0 1 1 1 1 1 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 1 1 0 0 0 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 0 0 0 0 1 1 0 0 1 1 1 1 1 0 0 0 0 1 1 1 0 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 1 0 0 1 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0
Would you detect, on looking at it, that it was not the result of “fair coins fairly tossed”? I’d say at first glance, it all looks pretty reasonable. Nor does it conform to any fancy number, like pi in binary. I defy anyone to find a pattern in that run. The reason I so defy you is that it was actually generated by a random process. I had no idea what the sequence was going to be before it was generated, and I’d generated another 99,999 of them before the loop finished. It is the result of a stochastic process, just as the first set were, but this time, the process was different. For this series, instead of randomly choosing the next outcome from an equiprobable “Heads” or “Tails” I randomly selected the length the next run of each toss-type from the values 1 to 5, with an equal probability of each length. So I might get 3 Heads, 2 Tails, 5 Heads, 1 Tail, etc. This means that I got far more runs of 5 Heads than I did the first time, but far fewer (infinitely fewer in fact!) runs of 6 Heads! So ironically, the lack of very long runs of Heads is the very clue that tells you that this series is not the result of the process “fair coins, fairly coins”.
But it IS a “chance” process, in the sense that no intelligent agent is doing the selecting, although in intelligent agent is designing the process itself – but then that is also true of the coin toss.
Now, how about this one?
Prizes for spotting the stochastic process that generated the series!
The serious point here is that by rejecting a the null of a specific stochastic process (fair coins, fairly tossed) we are a) NOT rejecting “chance” (because there are a vast number of possible stochastic processes). “Chance” is not the null; “fair coins, fairly tossed” is.
However, the second fallacy in the “500 coins” story, is that not only are we not rejecting “chance” when we reject “fair coins, fairly tossed”) but nor are we rejecting the only alternative to “Intelligently designed”. We are simply rejecting one specific stochastic process. Many natural processes are stochastic, and the outcomes of some have bell-curve probability distributions, and of others poisson distributions, but still others, neither. For example many natural stochastic processes are homeostatic – the more extreme some parameter becomes, the more likely is the next state to be closer to the mean.
The third fallacy is that there is something magical about “500 bits”. There isn’t. Sure if a p value for data under some null is less than 2^-500 we can reject that null, but if physicists are happy with 5 sigma, so am I, and 5 sigma is only about 2^-23 IIRC (it’s too small for my computer to calculate).
And fourthly, the 500 bits is a phantom anyway. Seth Lloyd computed it as the information capacity of the observable universe, which isn’t the same as the number of possible times you can toss a coin, and in any case, why limit what can happen to the “observable universe”? Do IDers really think that we just happen to be at the dead centre of all that exists? Are they covert geocentrists?
Lastly, I repeat: chance is not a cause. Sure we can use the word informally as in “it was just one of those chance things….” or even “we retained the null, and so can attribute the observed apparent effects to chance…” but only informally, and in those circumstances, “chance” is a stand-in for “things we could not know and did not plan”. If we actually want to falsify some null hypothesis, we need to be far more specific – if we are proposing some stochastic process, we need to put specific parameters on that process, and even then, chance is not the bit that is doing the causing – chance is the part we don’t know, just as I didn’t know when I ran my MatLab script what the outcome of any run would be. The part I DID know was the probability distribution – because I specified the process. When a coin is tossed, it does not fall Heads because of “chance”, but because the toss in question was one that led, by a process of Newtonian mechanics, to the outcome “Heads”. What was “chance” about it is that the tosser didn’t know which, of all possible toss-types, she’d picked. So the selection process was blind, just as mine is in all the above examples.
In other words it was non-intentional. That doesn’t mean it was not designed by an intelligent agent, but nor does it mean that it was.
And if I now choose one of those “chance” coin-toss sequences my script generated, and copy-paste it below, then it isn’t a “chance” sequence any more, is it? Not unless Microsoft has messed up (Heads=”true”, Tails=”false”):
true false true false false false false true true false true true false true true true false true false true true true true true false true false false false true true true true true true true true true false false false true true false true true false false false true false false true true false false false true false true false true true true true true true false false true false true true true true true true false true true true false true false false false false false false false false false false false false false false true false false true false true true true false true true true false true true false false true true true true true false true false true false false true true false true true true true true true true false false true false false true false false true true false true true true true false false true false false false false true false false true true false false true false true true false true false true true true true true true true true true true true true true false true false false true false false false true false false true true true false false true true true false true true true false false false true false true false false true false true false true true false true false true false true false false true true true false true true false false false false true false false true false true true true true true false true true true false false false true false true false true true true false false false false false false false true true false true false true false true true false false false true false true true false true false true true true true false true false false false false true false true true true true false false true false true true true true false true true false false true false true false true true true true true false false false true true true false false false true true true false true false true true true true true true true false false true false true false false true true true false true false true true false false true true true false true true false false false true false false false false true false false true true true true false false true false false true true true true false true false false true false true true false false true true false false true true false true false true true false false false false false false false true false true true false false false true true true false false false true false true false false false true true false true false true true true true false true false false false true false true true true false false false false true false true true false true true true false true true false true false false true false true false true true false false true false true false true false false true true false false
I specified it. But you can’t tell that by looking. You have to ask me.
ETA: if you double click on the images you get a clear version.
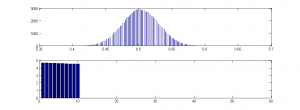
ETA2: Here’s another one – any guesses as to the process (again entirely stochastic)? Would you reject the null of “fair coins, fairly tossed”?
0 1 0 1 0 1 0 1 0 0 1 1 1 1 1 0 1 0 1 1 1 1 0 0 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 0 1 1 0 0 0 1 0 1 1 0 1 0 0 1 1 0 1 1 0 1 1 0 1 0 1 0 0 1 1 0 0 1 0 0 1 0 0 0 1 1 0 1 1 0 0 0 1 1 1 0 1 0 0 0 1 0 1 1 0 1 1 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 1 0 0 1 0 1 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 1 0 0 0 1 0 1 0 0 1 1 1 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 0 1 1 1 0 1 0 0 0 1 1 0 1 0 1 0 0 1 0 1 1 1 0 0 1 0 1 0 1 0 0 1 0 1 1 0 0 0 0 0 0 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0 1 1 1 0 1 0 0 0 0 1 1 1 0 1 0 0 1 0 1 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 1 0 0 1 1 1 1 0 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 0 0 1 0 0 0 1 0 1 1 0 1 0 1 1 0 1 1 1 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 0 0 1 1 0 1 0 1 0 1 0 0 0 1 0 1 0 1 1 1 1 0 0 1 0 1 0 1 1 1 0 1 0 0 1 0 0 1 1 1 0 0 1 1 0 0 1 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 1 1 0 1 1 0 0 0 1 0 1 1 0 0 1 1 0 1 0 0 1 0 0 1 1 1 0 1 0 0 1 0 1 0 1 0 1 1 0 1 0 1 1 0 0 1 1 1 0 1 0 0 0 0 1 0 1 1 1 1 0 1 0 0 0 1 1 1 0 0 1 1 0 1
Barry? Sal? William?
ETA3: And here’s another version:
The top plot is the distribution of proportions of Heads.
The second plot is the distribution of runs of Heads
The bottom two plots represent two runs; blue bars represent Heads.
What is the algorithm? Again, it’s completely stochastic.
And one final one:
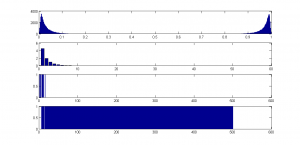 which I think is pretty awesome! Check out that bimodality!
which I think is pretty awesome! Check out that bimodality!
Homochirality here we come!!!

They are not “examples” of anything, because they don’t exist in any of the contexts you’ve proposed. Nor does anything remotely similar. If this is your best “evidence” for ID, all I can say is that you can only be sustained by absurdity.
Some of us are a little more interested in reality.