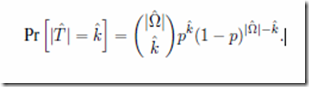(Preamble: I apologize in advance for cluttering TSZ with these three posts. There are very few people on either side of the debate that actually care about the details of this “conservation of information” stuff, but these posts make good on some claims I made at UD.)
Given a sample space Ω and a target T ⊆ Ω, Dembski defines the following information measures:
Endogenous information: IS ≡ -log2( P(T) )
Exogenous information: IΩ ≡ -log2( |T|/|Ω| )
Active information: I+ ≡ IΩ – IS = log2( P(T) / |T|/|Ω|)
Active information is supposed to indicate design, but in fact, the amount of active info attributed to a process depends on how we choose to mathematically model that process. We can get as much free active info as we want simply by making certain modeling choices.
Free Active Info via Individuation of Possibilities
Dembski is in the awkward position of having impugned his own information measures before he even invented them. From his book No Free Lunch:
This requires a measure of information that is independent of the procedure used to individuate the possibilities in a reference class. Otherwise the same possibility can be assigned different amounts of information depending on how the other possibilities in the reference class are individuated (thus making the information measure ill-defined).
He used to make this point often. But two of his new information measures, “endogenous information” and “active information”, depend on the procedure used to individuate the possible outcomes, and are therefore ill-defined according to Dembski’s earlier position.
To see how this fact allows arbitrarily high measures of active information, consider how we model the rolling of a six-sided die. We would typically define Ω as the set {1, 2, 3, 4, 5, 6}. If the goal is to roll a number higher than one, then our target T is {2, 3, 4, 5, 6}. The amount of active information I+ is log2(P(T) / (|T|/|Ω|)) = log2((5/6) / (5/6)) = 0 bits.
But we could, instead, define Ω as {1, higher than 1}. In that case, I+ = log2((5/6) / (1/2)) = .7 bits. What we’re modeling hasn’t changed, but we’ve gained active information by making a different modeling choice.
Furthermore, borrowing an example from Dembski, we could distinguish getting a 1 with the die landing on the table from getting a 1 with the die landing on the floor. That is, Ω = { 1 on table, 1 on floor, higher than 1 }. Now I+ = log2((5/6) / (1/3)) = 1.3 bits. And we could keep changing how we individuate outcomes until we get as much active information as we desire.
This may seem like cheating. Maybe if we stipulate that Ω must always be defined the “right” way, then active information will be well-defined, right? But let’s look into another modeling choice that demonstrates that there is no “right” way to define Ω in the EIL framework.
Free Active Info via Inclusion of Possibilities
Again borrowing an example from Dembski, suppose that we know that there’s a buried treasure on the island of Bora Bora, but we have no idea where on the island it is, so all we can do is randomly choose a site to dig. If we want to model this search, it would be natural to define Ω as the set of all possible dig sites on Bora Bora. Our search, then, has zero active information, since it is no more likely to succeed than randomly selecting from Ω (because randomly selecting from Ω is exactly what we’re doing).
But is this the “right” definition of Ω? Dembski asks the question, “how did we know that of all places on earth where the treasure might be hidden, we needed to look on Bora Bora?” Maybe we should define Ω, as Dembski does, to include all of the dry land on earth. In this case, randomly choosing a site on Bora Bora is a high-active-information search, because it is far more likely to succeed than randomly choosing a site from Ω, i.e. the whole earth. Again, we have changed nothing about what is being modeled, but we have gained an enormous amount of active information simply by redefining Ω.
We could also take Dembski’s question further by asking, “how did we know that of all places in the universe, we needed to look on Bora Bora?” Now it seems that we’re being ridiculous. Surely we can take for granted the knowledge that the treasure is on the earth, right? No. Dembski is quite insistent that the zero-active-information baseline must involve no prior information whatsoever:
The “absence of any prior knowledge” required for uniformity conceptually parallels the difficulty of understanding the nothing that physics says existed before the Big Bang. It’s common to picture the universe before the Big Bang is a large black void empty space. No. This is a flawed image. Before the Big Bang there was nothing. A large black void empty space is something. So space must be purged from our visualization. Our next impulse is then, mistakenly, to say, “There was nothing. Then, all of a sudden…” No. That doesn’t work either. All of a sudden presupposes there was time and modern cosmology says that time in our universe was also created at the Big Bang. The concept of nothing must exclude conditions involving time and space. Nothing is conceptually difficult because the idea is so divorced from our experience and familiarity zones.
and further:
The “no prior knowledge” cited in Bernoulli’s PrOIR is all or nothing: we have prior knowledge about the search or we don’t. Active information on the other hand, measures the degree to which prior knowledge can contribute to the solution of a search problem.
To define a search with “no prior knowledge”, we must be careful not to constrain Ω. For example, if Ω consists of permutations, it must contain all permutations:
What search space, for instance, allows for all possible permutations? Most don’t. Yet, insofar as they don’t, it’s because they exhibit structures that constrain the permissible permutations. Such constraints, however, bespeak the addition of active information.
But even if we define Ω to include all permutations of a given ordered set, we’re still constraining Ω, as we’re excluding permutations of other ordered sets. We cannot define Ω without excluding something, so it is impossible to define a search without adding active information.
Active information is always measured relative to a baseline, and there is no baseline that we can call “absolute zero”. We therefore can attribute an arbitrarily large amount of active information to any search simply by choosing a baseline with a sufficiently large Ω.
Returning our six-sided die example, we can take the typical definition of Ω as {1, 2, 3, 4, 5, 6} and add, say, 7 and 8 to the set. Obviously our two additional outcomes each have a probability of zero, but that’s not a problem — probability distributions often include zero-probability elements. Inclusion of these zero-probability outcomes doesn’t change the mean, median, variance, etc. of the distribution, but it does change the amount of active info from 0 to log2((1/6) / (1/8)) = .4 bits (given a target of rolling, say, a one).
Free Violations of the LCI
Given a chain of two searches, the LCI says that the endogenous information of the first search is at least as large as the active information of the second. Since we can model the second search to have arbitrarily large active information, we can always model it such that its active information is larger than the first search’s endogenous information. Thus any chain of searches can be shown to violate the LCI. (We can also model the first search such that its endogenous information is arbitrarily large, so any chain of searches can also be shown to obey the LCI.)