Evo-Info 4 addendum

Posted on by
Introduction to Evolutionary Informatics, by Robert J. Marks II, the “Charles Darwin of Intelligent Design”; William A. Dembski, the “Isaac Newton of Information Theory”; and Winston Ewert, the “Charles Ingram of Active Information.” World Scientific, 332 pages.
Classification: Engineering mathematics. Engineering analysis. (TA347)
Subjects: Evolutionary computation. Information technology–Mathematics.

In “Evo-Info 4: Non-Conservation of Algorithmic Specified Complexity,” I neglected to explain that algorithmic mutual information is essentially a special case of algorithmic specified complexity. This leads immediately to two important points:

  1. Marks et al. claim that algorithmic specified complexity is a measure of meaning. If this is so, then algorithmic mutual information is also a measure of meaning. Yet no one working in the field of information theory has ever regarded it as such. Thus Marks et al. bear the burden of explaining how they have gotten the interpretation of algorithmic mutual information right, and how everyone else has gotten it wrong.
  2. It should not come as a shock that the “law of information conservation (nongrowth)” for algorithmic mutual information, a special case of algorithmic specified complexity, does not hold for algorithmic specified complexity in general.

My formal demonstration of unbounded growth of algorithmic specified complexity (ASC) in data processing also serves to counter the notion that ASC is a measure of meaning. I did not explain this in Evo-Info 4, and will do so here, suppressing as much mathematical detail as I can. You need to know that a binary string is a finite sequence of 0s and 1s, and that the empty (length-zero) string is denoted \lambda. The particular data processing that I considered was erasure: on input of any binary string x, the output \mathtt{erased}(x) is the empty string. I chose erasure because it rather obviously does not make data more meaningful. However, part of the definition of ASC is an assignment of probabilities to all binary strings. The ASC of a binary string is infinite if and only if its probability is zero. If the empty string is assigned probability zero, and all other binary strings are assigned probabilities greater than zero, then the erasure of a nonempty binary string results in an infinite increase in ASC. In simplified notation, the growth in ASC is

    \[A(\mathtt{erased}(x)) - A(x) = \underbrace{A(\lambda)}_\text{infinite} - \underbrace{A(x)}_\text{finite} = \infty\]

for all nonempty binary strings x. Thus Marks et al. are telling us that erasure of data can produce an infinite increase in meaning.

In Evo-Info 4, I observed that Marks et al. had as “their one and only theorem for algorithmic specified complexity, ‘The probability of obtaining an object exhibiting \alpha bits of ASC is less then [sic] or equal to 2^{-\alpha},’” and showed that it was a special case of a more-general result published in 1995. George Montañez has since dubbed this inequality “conservation of information.” I implore you to understand that it has nothing to do with the “law of information conservation (nongrowth)” that I have addressed.

Now I turn to a technical point. In Evo-Info 4, I derived some theorems, but did not lay them out in “Theorem … Proof …” format. I was trying to make the presentation of formal results somewhat less forbidding. That evidently was a mistake on my part. Some readers have not understood that I gave a rigorous proof that ASC is not conserved in the sense that algorithmic mutual information is conserved. What I had to show was the negation of the following proposition:

(False)   \[A(f(x); c, P) - A(x; c, P) \leq K(f) + O(1) \]

for all binary strings x and c, for all probability distributions P over the binary strings, and for all computable [ETA 12/12/2019: total] functions f on the binary strings. The variables in the proposition are universally quantified, so it takes only a counterexample to prove the negated proposition. I derived a result stronger than required:

Theorem 1. There exist computable function f and probability distribution P over the binary strings such that

    \[A(f(x); c, P) - A(x; c, P) = \infty\]

for all binary strings c and for all nonempty binary strings x.

Proof. The proof idea is given above. See Evo-Info 4 for a rigorous argument.

In the appendix, I formalize and justify the claim that algorithmic mutual information is essentially a special case of algorithmic specified complexity. In this special case, the gain in algorithmic specified complexity resulting from a computable transformation f(x) of the data x is at most K(f) + O(1), i.e., the length of the shortest program implementing the transformation, plus an additive constant.

Appendix

Some of the following is copied from Evo-Info 4. The definitions of algorithmic specified complexity (ASC) and algorithmic mutual information (AMI) are:

    \begin{align*} A(x; c, P) &:= -\!\log P(x) - K(x|c) &\text{(ASC)} \\ I(x: c) &:= K(x) - K(x|c^*), &\text{(AMI)} \\ \end{align*}

where P is a distribution of probability over the set \mathcal{X} := \{0, 1\}^* of binary strings, x and c are binary strings, and binary string c^* is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity K(\cdot) and the conditional algorithmic complexity K(\cdot|\cdot) are defined, outputting c. The base of logarithms is 2. The “law of conservation (nongrowth)” of algorithmic mutual information is:

(1)   \begin{equation*} I(f(x) : c) \leq I(x:c) + K(f) + O(1) \end{equation*}

for all binary strings x and c, and for all computable [ETA 12/12/2019: total] functions f on the binary strings. As shown in Evo-Info 4,

    \[I(x: c) = -\!\log M(x) - K(x|c^*),\]

where the universal semimeasure M on \mathcal{X} is defined M(x) := 2^{-K(x)} for all binary strings x. Here we make use of the normalized universal semimeasure

    \[M^*\!(x) := \frac{M(x)}{M(\mathcal{X})},\]

where M(\mathcal{X}) = \sum_x M(x). Now the algorithmic mutual information of binary strings x and c differs by an additive constant, \log M(\mathcal{X}), from the algorithmic specified complexity of x in the context of c^* with probability distribution M^*.

Theorem 2. Let x and c be binary strings. It holds that

    \[I(x : c) = A(x; c^*\!, M^*) - \log M(\mathcal{X}).\]

Proof. By the foregoing definitions,

    \begin{align*} I(x : c) &= K(x) - K(x|c^*) \\ &= -\!\log M(x) - K(x|c^*) \\ &= -\!\log(M(\mathcal{X}) M^*\!(x)) - K(x|c^*) \\ &= -\!\log M^*\!(x) - K(x|c^*) - \log M(\mathcal{X}) \\ &= A(x; c^*, M^*) - \log M(\mathcal{X}). \end{align*}

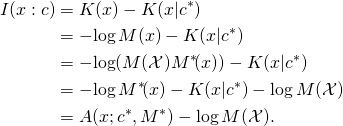
Theorem 3. Let x and c be binary strings, and let f be a computable [and total] function on \mathcal{X}. Then

    \[A(f(x); c^*\!, M^*) - A(x; c^*\!, M^*) \leq K(f) + O(1).\]

Proof. By Theorem 2,

    \begin{align*} &A(f(x); c^*\!, M^*) - A(x; c^*\!, M^*) \\ &\quad = [I(f(x) : c) - \log M^*\!(\mathcal{X})] - [I(x : c) - \log M^*\!(\mathcal{X})] \\ &\quad = I(f(x) : c) - I(x : c) \\ &\quad \leq K(f) + O(1). \\ \end{align*}

The inequality in the last step follows from (1).

153 thoughts on “Evo-Info 4 addendum”

  1. colewd: I believe Eric is claiming that information cannot be increased with an algorithmic process. I consider natural selection to be this type of process. Do you disagree?

    Of course. Changes of gene frequency in simple population genetics models, under natural selection, can bring one allele which has higher fitness from a low frequency to a high frequency. I believe you yourself have just acknowledged that. That is increase of, for example, specified information or equivalently, of functional information. By Dembski’s definition, by Szostak and Hazen’s defintions.

    (And don’t give me any of this crap about how there has to be a new mutation to have any increase of information. You weren’t going to do that, were you?)

    Now, where exactly do we find the magic theorem that says that these gene frequency changes can’t happen?

  2. Eric, today:

    There is no demonstration, empirical or mathematical, that ASC is not conserved, and the conservation has been proven in the Bio-C paper I wrote…

    Eric, November 17:

    Now, I agree with Tom that ASC is not strictly conserved under stochastic processing.

  3. colewd:
    Adapa,

    Are you claiming that natural selection explains the diversity of life?

    Are you running from your false claim evolutionary processes can’t produce new information?

  4. Joe Felsenstein: You are repeatedly proclaiming that there is some mathematical theorem somewhere saying that information cannot be “created” by natural evolutionary processes. Where is this theorem? The more we ask you to support your claims, the more you seem to go off to trying to divert us with discussion of whether natural selection explains the diversity of life.

    Just Bill being Bill.

  5. keiths: Eric, today:

    There is no demonstration, empirical or mathematical, that ASC is not conserved, and the conservation has been proven in the Bio-C paper I wrote…

    Eric, November 17:

    Now, I agree with Tom that ASC is not strictly conserved under stochastic processing.

    LOL! That’s gonna leave a mark. 🙂

  6. Joe Felsenstein,

    Of course. Changes of gene frequency in simple population genetics models, under natural selection, can bring one allele which has higher fitness from a low frequency to a high frequency. I believe you yourself have just acknowledged that. That is increase of, for example, specified information or equivalently, of functional information. By Dembski’s definition, by Szostak and Hazen’s defintions.

    How do you know information has been added with this process? You are assuming a correlation between fitness and information with this process. I think this is a big disconnect between your argument and Eric’s. His claim is that this process will not increase information based his analysis of algorithmic specified information. He is not making a claim about fitness. I do think that Eric’s claim has promise.

    That is increase of, for example, specified information or equivalently, of functional information.

    Here is the unsupported claim on your side.

  7. New post: “Non-conservation of algorithmic specified complexity…”

    … proved without reference to infinity and the empty string.

    Some readers have objected to my simple proof that computable transformation f(x) of a binary string x can result in an infinite increase of algorithmic specified complexity (ASC). Here I give a less-simple proof that there is no upper bound on the difference in ASC of f(x) and x. To put it more correctly, I show that the difference can be any positive real number.

    Here is what I prove:

    Theorem. Let f(x) = y be a constant function on \mathcal{X}. Let x and c be elements of \mathcal{X} for which K(x|c) > K(y|c) holds. Also let \alpha be a positive real number. There exists a distribution p of probability over \mathcal{X} such that

        \[A(f(x); c, p) - A(x; c, p) = \alpha.\]

    ETA: \mathcal{X} is the set of all binary strings.

  8. colewd: I do think that Eric’s claim has promise.

    Of course you do Bill. You’ll desperately cling to any pseudo-scientific garbage if it tells you what you want to hear.

  9. Tom English: ETA: Suppose you model the mitochondrial DNA in a eukaryotic cell as a binary string, and assign probabilities p(x) to binary strings. You might set p(λ) = 0 for the empty string λ. But if a cell divides, and one of the resulting cells gets none of the mitochondria, then the ASC of the mitochondrial DNA of that cell is infinite. That is, the mitochondrial DNA is represented by the empty string λ, and p(λ) = 0 implies infinite ASC.

    colewd: Why would this not be undefined vs infinity?

    Well, what I wrote before the addendum was that 1/p(x) approaches infinity as p(x) approaches zero. It is also commonly said that the limit is undefined. But we understand that the limit is undefined because there is no upper bound on how large the improbability 1/p(x) can be.

    You can change the probability p(λ) from zero to fabulously small. Then when cell reproduction results in a cell with no mitochondria, the ASC of the empty string λ representing the mitochondrial DNA is huge, though finite, according to your probabilistic model p. To repeat something I’ve told you before, the information is not “out there.” Historically, i.e., beginning with Dembski, the use of specified complexity is to reject probabilistic models (“chance hypotheses”).

  10. Tom English,

    ASC is probabilistic. Although a positive ASC score could signify meaning, a positive score can also be achieved by chance. The probability of achieving at least α bits of ASC by chance is at most 2−α [1]. The improbability of ASC has been generalized for any canonical specified complexity in [28], where the criterion of canonical specified complexity as possession of a kardis is also defined in [28].

    Is this consistent with the proof you just posted?

  11. colewd: How do you know information has been added with this process? You are assuming a correlation between fitness and information with this process. I think this is a big disconnect between your argument and Eric’s. His claim is that this process will not increase information based his analysis of algorithmic specified information. He is not making a claim about fitness. I do think that Eric’s claim has promise.

    [me:]

    That is increase of, for example, specified information or equivalently, of functional information.

    colewd
    Here is the unsupported claim on your side.

    Nope, nothing is unsupported in what I wrote. Dembski himself (NFL, 2002) said that specification could be “cashed out” in terms of viability and other quantities related to fitness. That is what I did, used a fitness scale, on which the specification is the region of highest fitness. It’s also a Functional Information calculation if you choose fitness as the “function”. Which one is allowed to do. The other functions that people use with FI are all ones that are assumed to correlate with fitness.

    So the issue you raise is nonexistent.

  12. DNA_Jock: Your Bio-C paper does not even purport to demonstrate that ASC cannot increase. You work with expected ASC, the biological relevance of which is nil.

    Well, Nemati and Holloway do not explain themselves clearly. Section 4 of the paper, evidently written by Holloway, does not belong in a paper titled “Expected Algorithmic Specified Complexity.” When the authors say in Section 4.2 (see the annotation of the passage attached to this comment) that “we establish the conservation of complexity for ASC,” what they actually show is that

        \begin{align*} f\!ASC(x, C, p, f) &= -\!\log_2 \sum_{z:f(z)=f(x)} p(z) - K(f(x)|C) \\ &< -\!\log_2 \sum_{z:f(z)=f(x)} p(z) \\ &\leq -\!\log_2 p(x). \end{align*}

    This bound on fASC says nothing about [their notation]

    (*)   \[ASC(f(x), C, p) = -\!\log_2 p(f(x)) - K(f(x)|C) .\]

    In my counterexample of f(x) = \lambda for all x, and p(\lambda) = 0, the first term in fASC (the negative log-sum) is equal to zero, and the first term in (*) is infinite. Thus there’s a whole helluva lot of difference between fASC and ASC. As I showed in another screen grab, above, what immediately follows the passage I show below is a naked assertion of a relation of fASC to ASC. I cannot believe that Holloway believes that he has proven anything about ASC in Section 4.

  13. colewd:

    ASC is probabilistic. Although a positive ASC score could signify meaning, a positive score can also be achieved by chance. The probability of achieving at least α bits of ASC by chance is at most 2−α [1]. The improbability of ASC has been generalized for any canonical specified complexity in [28], where the criterion of canonical specified complexity as possession of a kardis is also defined in [28].

    Is this consistent with the proof you just posted?

    I’d say that’s logically independent of my new theorem. But I will take this opportunity to point out that Nemati and Holloway show in the following that they have not grasped the formal details of the inequality they state informally in the passage you quote.

    Finally, as a corollary, using the new label random variable defined as

    (44)   \[L := f(\mathcal{X}) \]

    […]

    Additionally, since we are dealing with a random variable the improbability of ASC still applies,

    (46)   \[\Pr[ASC(l, C, p) > \alpha] \leq 2^{-\alpha}. \]

    Now, they must have meant to write L instead of l in (46):

    (46*)   \[\Pr[ASC(L, C, p) > \alpha] \leq 2^{-\alpha}. \]

    The problem is that (46*) holds if random variable L = f(\mathcal{X}) has p as its probability distribution. But it is the random variable \mathcal{X} that is distributed according to p. It is not generally the case that f(\mathcal{X}) has the same distribution as \mathcal{X}. This indicates horrible confusion on the part of the authors. They might have discovered that they were mixed up, had they tried to prove (46). But all that they did was to assert it (calling it a corollary, as though that obviated the need to supply a proof).

  14. I had taken equations 41, 42 and 43 to be talking about the expected value of the ASC over all x. That is to say, I had assumed that the authors had made a simple error in annotation, using x when they meant X, eerily similar to the annotation error that you made here in 2018 (in the fifth black box), and only recently (10/30/19) corrected.

  15. Joe Felsenstein,

    Nope, nothing is unsupported in what I wrote. Dembski himself (NFL, 2002) said that specification could be “cashed out” in terms of viability and other quantities related to fitness. That is what I did, used a fitness scale, on which the specification is the region of highest fitness. It’s also a Functional Information calculation if you choose fitness as the “function”. Which one is allowed to do. The other functions that people use with FI are all ones that are assumed to correlate with fitness.

    So the issue you raise is nonexistent.

    The working assumption is that fitness correlates with function in your model. I would call it a micro evolutionary model as improved fitness is very different then building a unique new feature.

  16. Tom English,

    I’d say that’s logically independent of my new theorem. But I will take this opportunity to point out that Nemati and Holloway show in the following that they have not grasped the formal details of the inequality they state informally in the passage you quote.

    What they claim is the expected value of ASC is negative. Do you dispute this claim?
    Have you reviewed the empirical test they did. Any thoughts?

  17. colewd: His claim is that this process will not increase information based his analysis of algorithmic specified information.

    Which is of course obviously absurd. If you could somehow show that “algorithmic specified information” could not evolve, then all you would have managed to show is that “algorithmic specified information” is not applicable to genetics.

    If some gene-sequence S has some information I, and mutation X of string S has information >I, then the process of mutation can create information when and if S is mutated to Sx. And if mutant string Sx has higher fitness than S, then natural selection can make Sx go to high frequency in the population, thus increasing information in the genome of the population. So evolution can OBVIOUSLY create new information in the genome.

    Look, all Eric’s mindless math-babble is so obviously false it boggles the mind how anyone could possibly be persuaded by it. It’s a smokescreen. It sounds fancy and technical, but it’s vacuous blather designed to impress people who don’t bother to really think about it.

    Evolution can’t not produce information in the genome, insofar as information is in any way dependent on genetic sequences. If information is related to what the sequence is, then information can be produced by mutation of a sequence. And if different alleles have different fitnesses, natural selection can bring it to fixation in some population.

    How can someone fail to grasp these incredibly simple, elementary concepts?

  18. Rumraket: Look, all Eric’s mindless math-babble is so obviously false it boggles the mind how anyone could possibly be persuaded by it. It’s a smokescreen. It sounds fancy and technical, but it’s vacuous blather designed to impress people who don’t bother to really think about it.

    That’s our Bill! He never met any anti-science woo he didn’t like. 🙂

  19. colewd: The working assumption is that fitness correlates with function in your model. I would call it a micro evolutionary model as improved fitness is very different then building a unique new feature.

    What function will that new feature serve, I wonder, if it does not support viability, survival, reproduction or any other fitness component?

  20. Dr. English, why do you skip my discussion in the paper where I explain why it is necessary to use fASC to coherently deal with stochastic processing? Of course, if you cut out the context, then it is unclear how fASC is related to ASC.

    As I’ve stated a couple times, you are either showing that ASC functions as intended since you are modifying the probability distribution/domain/whatever you want to call it with your function application, or you need to be modifying the random variable underlying the probability distribution, in which case you end up with my fASC construct, and the related conservation bounds.

    Seriously, it seems you are being purposefully obtuse in this discussion just in an attempt to ignore the point of our Bio-C paper. If you are truly making an honest attempt to engage with the paper, then explain why you disagree with my discussion in the Bio-C paper about why the random variable needs to be modified, and why fASC needs to be used to deal with the scenario you are trying to address in the OPs. Otherwise, I fail to see the point in all your OPs, besides the obvious that you look for any opportunity to try and make our work look bad, all while ignoring the substance of the work. In which case, what is the point in my participation in this forum? I expect at least a little scholarly professionalism in criticism.

    To the general reader, I recommend at least skimming the Bio-C paper to get context on what’s going on here.

  21. Rumraket: Look, all Eric’s mindless math-babble is so obviously false it boggles the mind how anyone could possibly be persuaded by it.

    Please identify the mathematical error, and send it to Bio-C as a criticism. Or, at the very least, post it in a comment. Otherwise you are also just engaging in pointless ad hominem.

  22. EricMH: Please identify the mathematical error

    Oh I see I misstated what I intended to convey. I should not have said that your math was false, but that the conclusions you attempt to draw from it when you argue it can be applied to biology, is.

    The question is not whether you’re able to correctly solve equations, the question is if your math relates to something that happens in real biology. And it does not.

    For reasons already stated to Bill, if you could somehow show that “algorithmic specified information” could not evolve, then all you would have managed to show is that “algorithmic specified information” is not applicable to something real in genetics.

    Because the actual gene-sequences we see in living organisms are obviously evolvable entities. Again, for reasons already stated.

  23. EricMH: Please identify the mathematical error, and send it to Bio-C as a criticism.

    Please identify how your math is applicable to anything in actual biology and submit it to any reputable scientific journal.

  24. I see a paper published wherein scientists describe a process that shows that some enzyme was duplicated, it subsequently mutated, and some small chemical reaction that was useful, was being selected for to increase. Where before there was one gene, there’s now two. Where before only one function was being utilized, now there’s two being utilized.

    This happened, in the real world.

    Now EricMH comes along and says he has a theorem that says information can’t be created by evolution. And I just have to realize that what EricMH says then has nothing of relevance to say about real biological evolution. If EricMH’s theorem says new information can’t evolve, yet I can see in the real world that new functional gene sequences do so, then whatever it is EricMH thinks he is doing when he defines information, and “proves” it can’t evolve, has zero relevance to the real world.

    Then nobody should care about EricMH’s ideas about information. Because we don’t really care about Eric’s nebulous information concepts, we care about the properties of real living organisms. The molecules that actaully make them up. Where did that stretch of DNA come from? How? What does it do?

  25. Rumraket: Then nobody should care about EricMH’s ideas about information. Because we don’t really care about Eric’s nebulous information concepts, we care about the properties of real living organisms. The molecules that actaully make them up. Where did that stretch of DNA come from? How? What does it do?

    Yep. EricMH’s folly reminds me of the urban legend about how an engineer once mathematically “proved” bumblebees can’t fly. That was just before one flew up and stung him on the ass. 😀

  26. colewd: The working assumption is that fitness correlates with function in your model.

    No. That the traits we use for the scale in CSI arguments, or in FI arguments, are adaptations that increase fitness is implicit in everyone’s arguments about CSI and FI. Not just in “your [my] model”.

    I would call it a micro evolutionary model as improved fitness is very different then building a unique new feature.

    All the FI and CSI arguments work that way. So I guess that you would call all of them “micro evolutionary”.

    Thank you for correcting me, based on your years of experience in making mathematical arguments in biology.

  27. Corneel,

    What function will that new feature serve, I wonder, if it does not support viability, survival, reproduction or any other fitness component?

    This is an interesting question. Is there any correlation between between simple adaption (antibiotic resistance) and complex adaption flight, sight etc. Eric’s math if correct puts doubt in evolutions (algorithmic process) ability to consistently increase genetic information which is required for complex adaptions.

  28. colewd: Eric’s math if correct puts doubt in evolutions (algorithmic process) ability to consistently increase genetic information which is required for complex adaptions.

    Since evolution’s algorithmic processes are empirically observed to consistently increase genetic information that means EricMH’s claims are wrong. His math may be fine but it’s not applicable to reality in biological life.

    The real question is how long will you keep beating this dead horse?

  29. Joe Felsenstein,

    All the FI and CSI arguments work that way. So I guess that you would call all of them “micro evolutionary”.

    Do you think Behe’s or gpuccio’s arguments work primarily connecting function to fitness or fitness to genetic information?

  30. colewd,

    Joe Felsenstein,

    Do you think Behe’s or gpuccio’s arguments work primarily connecting function to fitness or fitness to genetic information?

    Behe’s arguments, as you ought to know, are totally different, so let’s set them aside.

    gpuccio has no valid arguments, at least none based on anything like CSI or ASC. He ends up saying that it’s an empirical matter, and does not present any theoretical argument. As you ought to know, but I suspect don’t know.

  31. Joe Felsenstein,

    Behe’s arguments, as you ought to know, are totally different, so let’s set them aside.

    gpuccio has no valid arguments, at least none based on anything like CSI or ASC. He ends up saying that it’s an empirical matter, and does not present any theoretical argument. As you ought to know, but I suspect don’t know.

    How much have you read Behe’s work or gpuccio’s articles? Where these comments appear off is based on Behe’s edge of evolution and several of gpuccio’s articles where he references Dembski’s work.

    While I agree that Gpuccio does not bring a unique theoretical argument to the table the empirical evidence he provides is quite unique and interesting.

    The bottom line is the design argument does not require fitness as a means to drive information into the population.

  32. colewd: The bottom line is the design argument does not require fitness as a means to drive information into the population.

    The real bottom line is empirically observed evolutionary processes don’t need a magic Designer or a disembodied mind to get new information into a population.

  33. colewd: he bottom line is the design argument does not require fitness as a means to drive information into the population.

    Or another way to make Adapa’s point: yes, colewd is right. The Design argument does not require differences in fitness, or anything like that. Just a Designer who can go “Poof!”

  34. colewd: Is there any correlation between between simple adaption (antibiotic resistance) and complex adaption flight, sight etc.

    Yes, they are all adaptations that increase fitness.

    You have, at many times, referred to the ability of purifying selection to conserve the sequence of certain proteins for millions of years. This is an implicit appeal to a process that drives populations toward high fitness (through high viability): It is not the Designer that actively maintains the sequence, but the selective elimination of mutant alleles that result in reduced organismal viability, i.e. natural selection. The same story goes for all adaptations that you’ve mentioned above.

    colewd: Eric’s math if correct puts doubt in evolutions (algorithmic process) ability to consistently increase genetic information which is required for complex adaptions.

    Eric’s math, if applicable to biological systems, makes it impossible for natural processes to fix any adaptation in a population, whether it is simple, medium complex or highly complex. That is how we know that Eric’s math cannot be relevant to evolutionary biology. After all, even you acknowledge that simple adaptations (like antibiotic resistance) don’t need intervention by an outside Agent. If simple adaptations can’t be stopped from fixing, then nothing in Eric’s math can stop the gradual accumulation of beneficial alleles resulting in complex (> 500 bits) information.

  35. EricMH: Dr. English, why do you skip my discussion in the paper where I explain why it is necessary to use fASC to coherently deal with stochastic processing?

    HI Eric:
    If I understand you correctly here, you are saying that you want to deal with the general case of f(x) being stochastic and to do so you first need the result you claim for the deterministic case in section 4.2.

    I had the same impression as Tom; for me, this was because the introduction to section 4 positions it as dealing with infinite p(f(x)). For me it would have been helpful to explicitly mention that the result be first be used to deal with both infinite probability for deterministic f() and then will be applied to investigate the general case of stochastic f().

  36. EricMH: aper about why the random variable needs to be modified, and why fASC needs to be used to deal with the scenario you are trying to address in the OPs.

    I am unclear on why you claim on p. 8 that

    “Thus, according to Equation (37) applying a function to a random variable can only produce a new set of labels that have an equal or greater probability than the old set of labels.”

    In the case under consideration, the sum is over the empty set, or if you prefer the sum is over elements of the domain that have zero probability. So does that not invalidate your claim?

    Now perhaps you would like to constrain of f to elements x which s.t. y=f(x) has non-zero probability. But in that case, why couldn’t y=f(x) be another element of X that has smaller probability that x?

    Also, I don’t understand how you can ignore K(f(x)|C) for the general case. Is it not possible that any increase in the probability for f(x) will be more than offset by a decrease in K(f(x)|C) so that overall ASC will increase?

    In fact, as I understand it, Tom’s latest OP on non-empty string deals with that type of situation. That is, he is showing that for a specific context c, there is a probability distribution for x that will lead to increase of ASC for f(x).
    (ETA: last sentence)

  37. Rumraket: If some gene-sequence S has some information I, and mutation X of string S has information >I, then the process of mutation can create information when and if S is mutated to Sx

    When you say information, what specifically are you referring to. Is it ASC?

    I do agree with you overall that math proofs on their own have nothing to do with science. Instead, the math has to be part of some model that is proposed to capture a real world process.

    In the case of modeling the NS mechanism, I don’t think we should look at modeling the mutation of a single genome. Rather, we should try to understand how some overall measure of information of a population of genomes with respect to a given niche can be increased by NS. For ASC, the idea would be to use the Context C to somehow capture the niche and to use the x to model all the genomes, eg as a concatenated bit string.

    Similar concerns were raised for an OP by Eric where he tried to apply his usage of Levin’s results on Kolmogorov Mutual Information to building a biological model. There he worked with single genome and the version of f() he used there did not account for the niche and its role in selection.

    As a general point on several of your posts: I don’t think Eric is denying the fact of evolution. Rather, he uses the fact of evolution to claim that his results showing the impossibility of evolution by stochastic process prove that intelligence must be involved. Eric believes intelligence is not constrained to rely on stochastic processes.

  38. BruceS: For ASC, the idea would be to use the Context C to somehow capture the niche and to use the x to model all the genomes, eg as a concatenated bit string.

    Ooooh. I would love Eric to translate the model to real-life, like you just did. As I currently understand it, c is supposed to be a target genome and x some genome we wish to examine. ASC expresses the log-ratio of the probability that some natural process transforms c to x over the probability that some natural process comes up with x without context c. The former somehow depends on the compressibility of x in terms of c.

    Close?

  39. Rumraket: Look, all Eric’s mindless math-babble is so obviously false it boggles the mind how anyone could possibly be persuaded by it. It’s a smokescreen. It sounds fancy and technical, but it’s vacuous blather designed to impress people who don’t bother to really think about it.

    EricMH: Please identify the mathematical error, and send it to Bio-C as a criticism. Or, at the very least, post it in a comment. Otherwise you are also just engaging in pointless ad hominem.

    When Rumraket speaks in generalities, Eric demands mathematical details. When I provide mathematical details, Eric speaks in generalities:

    EricMH: Dr. English, why do you skip my discussion in the paper where I explain why it is necessary to use fASC to coherently deal with stochastic processing? Of course, if you cut out the context, then it is unclear how fASC is related to ASC.

    […]

    To the general reader, I recommend at least skimming the Bio-C paper to get context on what’s going on here. [emphasis added]

    Eric Holloway is bluffing. The context that I supposedly omitted does not exist.

    Evidently Captain Holloway is desperate to save face with any “general reader” (read: IDer) who happens to be following this thread. He has accused me of misrepresenting his work by omitting essential context. The “general reader” should understand that Captain Holloway, in the time he spent railing against me, easily could have supplied the context — if it existed, anyway.

    The “general reader” should take note of the fact that Captain Holloway, rather than identify the particular section of the article that explains “why it is necessary to use fASC to coherently deal with stochastic processing” and makes it clear “how fASC is related to ASC,” recommends skimming the entire article. Don’t be fooled by his gambit: if what he says is in the article were in the article, then he would have told you where to find it.

    The “general reader” should not be shocked to hear that, in mathematical reasoning, we formally prove that propositions are true or false. Accompanying explanations are nice, to help readers understand the proofs and the significance of the results. But the explanations, in themselves, count for nothing as mathematics. However Captain Holloway might explain the equality labeled “bald assertion” in the attached screenshot, he will not have proved it. As I told him in a comment above, I already have proofs that his claims are wrong, but insist that he, having published assertions without proofs, go first. The burden is on him either to supply formal proofs, or to admit that he cannot.

    Now, it may appear, below, that Captain Holloway has justified the inequalities in (45) and (46). But simply asserting that a theorem applies is not justification. Every theorem is derived under certain assumptions, and for a theorem to apply in some circumstance, its assumptions must hold. You can see for yourself that Captain Holloway has not mentioned the assumptions. Of course, what I am doing now is to explain how he went wrong. The annotated passages that I’ve included on this comment page come from a forthcoming post that will supply proof that he is wrong.

    Stay tuned to see what Eric Holloway does. I’ll wager that he waits to see my proofs, without offering any of his own, and then explains that mine are wrong. But he may instead invoke a new rule that he’s made up in this thread: if you don’t submit your criticism to Bio-Complexity, then it doesn’t count.

  40. BruceS: Similar concerns were raised for an OP by Eric where he tried to apply his usage of Levin’s results on Kolmogorov Mutual Information to building a biological model. There he worked with single genome and the version of f() he used there did not account for the niche and its role in selection.

    That post was largely incoherent. It may not have seemed that way to you. But I know the definitions that Eric was trampling.

    You studied math as an undergrad — right? In my forthcoming OP, I ask readers to join me in scrutinizing Section 4.1, “Random Variables.” For once, there will be a number of folks who can see for themselves that Eric has a horrible grasp of mathematics. That will make me feel a bit less lonely.

    Corneel: As I currently understand it, c is supposed to be a target genome and x some genome we wish to examine.

    Excuse me for jumping in uninvited. Marks et al. usually characterize the context C as representing background knowledge.

    Corneel: ASC expresses the log-ratio of the probability that some natural process transforms c to x over the probability that some natural process comes up with x without context c. The former somehow depends on the compressibility of x in terms of c.

    Close?

    That’s right, but you should keep it in mind that the former distribution is not regularized (normalized). The probabilities sum to less than 1. Also, the IDists do not interpret the former as a probability distribution. As you saw, up the thread, Eric wants to reject the hypothesized distribution p in favor of intervention by an intelligent agent, not in favor of an alternative model. Marks, Dembski, and Ewert, at least in their book, have stopped referring to p as the chance hypothesis. They call p the intrinsic probability, or some such, and do not talk about rejecting it, as Dembski long did (famously expressing it as P(T|H)). I suspect that they realized that treating p as a chance hypothesis doesn’t make much sense when you’re saying that ASC is a measure of meaningful information. Eric Holloway hasn’t caught on yet.

    I think it makes sense to view ASC in terms of Neyman-Pearson hypothesis testing. So does Joe Felsenstein. We agree that the log transformation of the ratio is gratuitous.

  41. Corneel,

    Eric’s math, if applicable to biological systems, makes it impossible for natural processes to fix any adaptation in a population, whether it is simple, medium complex or highly complex. That is how we know that Eric’s math cannot be relevant to evolutionary biology. After all, even you acknowledge that simple adaptations (like antibiotic resistance) don’t need intervention by an outside Agent. If simple adaptations can’t be stopped from fixing, then nothing in Eric’s math can stop the gradual accumulation of beneficial alleles resulting in complex (> 500 bits) information.

    Two issue
    -A simple adaption can occur with existing information
    -A beneficial allele does not inform you about the change in information in the system.

  42. Also, the context C is unnecessary, if all it is is the general background knowledge necessary to say that this mathematics models some biological situation. And if that doesn’t change. (In the original KCS machinery I think C is the computing system on which the programs are being run, but that seems unrelated to the notion of general background knowledge used by Holloway).

    PS: a new post by me will appear today at Panda’s Thumb on why ASC is irrelevant to establishing any limits on adaptation.

  43. Tom English,

    That’s right, but you should keep it in mind that the former distribution is not regularized (normalized). The probabilities sum to less than 1. Also, the IDists do not interpret the former as a probability distribution. As you saw, up the thread, Eric wants to reject the hypothesized distribution p in favor of intervention by an intelligent agent, not in favor of an alternative model. Marks, Dembski, and Ewert, at least in their book, have stopped referring to p as the chance hypothesis. They call p the intrinsic probability, or some such, and do not talk about rejecting it, as Dembski long did (famously expressing it as P(T|H)). I suspect that they realized that treating p as a chance hypothesis doesn’t make much sense when you’re saying that ASC is a measure of meaningful information. Eric Holloway hasn’t caught on yet.

    Is what is being rejected an algorithmic process?

  44. Corneel: As I currently understand it, c is supposed to be a target genome and x some genome we wish to examine.

    Caveat: I don’t claim any expertise on the math involved in ASC or the biology involved in NS, so if something I post seems hokey, it probably is. With that in mind, thanks for the opportunity to pontificate.

    I am not aware of Eric making any attempt to translate the math of ASC in general to biology. He has attempted the special case of using Algorithmic Mutual Information to develop a biological model in the post he did at TSZ. He was only working there with a single genome, as I recall, which I continue to see as wrong. Here is his post:

    Mutual Algorithmic Information, Information Non-growth, and Allele Frequency

    Now no one is questioning the math of the conservation of mutual information that this post uses. It’s a standard math result, not an ID proponent’s claim. My concern was that if you captured the biology property, the math result would not apply.

    Now move on to ASC. First, note that Tom is questioning the mathematics of the claim of conservation of ASC in Eric’s paper.

    But putting that aside, my suggestion for trying to use ASC to model NS is that the context C must somehow capture the context provided in the environment that matters to the organism. (ie its niche) So C would be some bit string that captures that (how to make it a bit string? I dunno). The bit string x would represent the aggregate population genome. And the function f(x) would try to capture how NS transforms x to the descendent population’s aggregate genome.

    I don’t think mutation matters for the first step. What is important is to try to see if NS can increase ASC in that model of NS.

    I’ve seen the informal claim that NS transfers information from the environment to the population genome. The above is putting that in terms of ASC.

  45. BruceS,

    I don’t think mutation matters for the first step. What is important is to try to see if NS can increase ASC in that model of NS.

    I’ve seen the informal claim that NS transfers information from the environment to the population genome. The above is putting that in terms of ASC.

    I think what has been agreed upon by most is that natural selection can fix in the population modified existing information or copy existing information that already exists.

    I would say that this information must pre exist in linear sequential form ie a DNA or AA sequence.

    The bottom line is that natural selection can algorithmically copy and fix pre existing information in the population.

  46. Tom English: That post was largely incoherent. It may not have seemed that way to you. But I know the definitions that Eric was trampling.

    You studied math as an undergrad

    Yes, and that interest remains which is why I enjoy these posts.
    You are right that, at my level of understanding, I did not see the incoherence of the math in Eric’s previous post. So I’m happy to try to develop a deeper understanding of the math from your posts and interchanges with Eric.

    Just in terms of the claims in Eric’s paper, is the following correct:
    1. Equation 16 is based on standard results and is fine.
    2. Equation 43 is making a claim about deterministic f for any single x Your counter-examples of the empty set and in your latest post are meant to show that claim is false.
    3. Equation 45 and 46 are making claims about expected value(s) for X and f(X) which you dispute because the probability distribution for the expectation is not properly understood.

    I have not seen anything explicit about the claims the expectation for stochastic f applied to fixed x in 4.3 and for the claims about expectation applied over both stochastic f applied to X in 4.4. I assume you think those fail because the are based on the previous work in the paper.

    I have also not seen any concerns with the hypothesis testing results in 3.3. They look less than rigourous to me, eg where is the distribution of the test statistic (OASC): all I see is a claim about its expected value. For a test statistic, I am used to seeing the probability of all test statistic values at least as usual as the observed one; I don’t see how that idea is reflected in 3.3.

  47. BruceS, Corneel,

    The way that Milosavljević approximates algorithmic mutual information (essentially a special case of ASC) is to design a special encoder (compressor) of DNA sequences. My memory of the details is hazy, but I think what he does is to use one sequence (in what Marks et al. call the context) to compress another. The reason that this excites the IDists is that his general approach is just the same as theirs. The length of DNA sequence x when compressed using the other sequence is an upper bound on K(x|c). Of course, Milosavljević is not saying that the algorithmic mutual information of two DNA sequences is meaningful information.

    From Evo-Info 4:

    _______________

    Marks et al. furthermore have neglected to mention that Dembski developed the 2005 precursor (more general form) of algorithmic specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. Amusingly, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting \alpha bits of ASC is less then or equal to 2^{-\alpha},” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.

    According to the abstract of Milosavljević’s article:

    We explore applicability of algorithmic mutual information as a tool for discovering dependencies in biology. In order to determine significance of discovered dependencies, we extend the newly proposed algorithmic significance method. The main theorem of the extended method states that d bits of algorithmic mutual information imply dependency at the significance level 2^{-d+O(1)}.

    However, most of the argument — particularly, Lemma 1 and Theorem 1 — applies more generally. It in fact applies to algorithmic specified complexity, which, as we have seen, is defined quite similarly to algorithmic mutual information.

  48. colewd: I think what has been agreed upon by most is that natural selection can fix in the population modified existing information or copy existing information that already exists

    I am not really sure if I understand what you are saying, but it seems like it takes us back to a fine tuning argument: ie that the initial conditions and the laws of nature need to be fine tuned to allow that transfer of information via NS.

    That moves the issue from biology to cosmology. There I would agree that a deistic designer is a reasonable idea.

  49. BruceS: You are right that, at my level of understanding, I did not see the incoherence of the math in Eric’s previous post. So I’m happy to try to develop a deeper understanding of the math from your posts and interchanges with Eric.

    I do not mean to denigrate you. You’re a really bright guy. And, I guarantee you, there are areas of math that you know much better than I do. Algorithmic information theory is specialized knowledge. The basic idea is simple, but there are some longish chains of subjects that get you to a real understanding of the subject. I wouldn’t say that I’ve gotten there myself. The proofs I’ve posted are not much more than manipulation of definitions — nothing deep.

  50. Corneel: ASC expresses the log-ratio of the probability that some natural process transforms c to x over the probability that some natural process comes up with x without context c.

    Apologies if you are already famility with the following.

    ASC and Eric’s claims about it are just math. A biological context is outside the scope of the paper.

    Concerning the log ratio: It’s true that one can express ASC as a log ratio. But I found it easier to understand the concept starting with the basic definition given by equation (10). For a specified bitstring x sampled from a probability distribution p(X), ASC is -log2 p(x) MINUS K(x|C) — the Kolmogorov complexity conditional on a context C.

    There are earlier threads in TSZ raising concerns with that concept that Keith and Tom contributed heavily to; I can track them down if you don’t recall the ones I mean.

    Now to get from that MINUS get to the log ratio, you have to involve the so-called universal distribution. It puts the negative Kolmogorov complexity -K(x|C) into a exponent of 2 — see equation 14. Now you can take -log2(p(x)) + log2(2^-K(x)) to get a log ratio with the p(x) in the denominator. That idea (along with the Kraft inqueality) is used in the calcluation of expected value at start of 3.2.

    If you are interested in more on Kolmogorov complexity, the Kraft inequality, universal distribution and other math ideas in Eric and Tom’s posts, then the following paper is great. It is also about why tossing all-heads from an unbiased coin seems unusual, even though the probability of that particular sequence is no different from any other sequence.
    https://www.researchgate.net/publication/225562683_The_miraculous_universal_distribution

Leave a Reply