Subjects: Evolutionary computation. Information technology–Mathematics.
The greatest story ever told by activists in the intelligent design (ID) socio-political movement was that William Dembski had proved the Law of Conservation of Information, where the information was of a kind called specified complexity. The fact of the matter is that Dembski did not supply a proof, but instead sketched an ostensible proof, in No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002). He did not go on to publish the proof elsewhere, and the reason is obvious in hindsight: he never had a proof. In “Specification: The Pattern that Signifies Intelligence” (2005), Dembski instead radically altered his definition of specified complexity, and said nothing about conservation. In “Life’s Conservation Law: Why Darwinian Evolution Cannot Create Biological Information” (2010; preprint 2008), Dembski and Marks attached the term Law of Conservation of Information to claims about a newly defined quantity, active information, and gave no indication that Dembski had used the term previously. In Introduction to Evolutionary Informatics, Marks, Dembski, and Ewert address specified complexity only in an isolated chapter, “Measuring Meaning: Algorithmic Specified Complexity,” and do not claim that it is conserved. From the vantage of 2018, it is plain to see that Dembski erred in his claims about conservation of specified complexity, and later neglected to explain that he had abandoned them.
Algorithmic specified complexity is a special form of specified complexity as Dembski defined it in 2005, not as he defined it in earlier years. Yet Marks et al. have cited only Dembski’s earlier publications. They perhaps do not care to draw attention to the fact that Dembski developed his “new and improved” specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. That’s obviously quite different from their current presentation of algorithmic specified complexity as a measure of meaning. Ironically, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then [sic] or equal to
bits of ASC is less then [sic] or equal to ![]() ” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
Lately, a third-wave ID proponent by the name of Eric Holloway has spewed mathematicalistic nonsense about the relationship of specified complexity to algorithmic mutual information. [Note: Eric has since joined us in The Skeptical Zone, and I sincerely hope to see that he responds to challenges by making better sense than he has previously.] In particular, he has claimed that a conservation law for the latter applies to the former. Given his confidence in himself, and the arcaneness of the subject matter, most people will find it hard to rule out the possibility that he has found a conservation law for specified complexity. My response, recorded in the next section of this post, is to do some mathematical investigation of how algorithmic specified complexity relates to algorithmic mutual information. It turns out that a demonstration of non-conservation serves also as an illustration of the senselessness of regarding algorithmic specified complexity as a measure of meaning.
Let’s begin by relating some of the main ideas to pictures. The most basic notion of nongrowth of algorithmic information is that if you input data ![]() to computer program
to computer program ![]() then the amount of algorithmic information in the output data
then the amount of algorithmic information in the output data ![]() is no greater than the amounts of algorithmic information in input data
is no greater than the amounts of algorithmic information in input data ![]() and program
and program ![]() added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image
added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image ![]() by a program
by a program ![]() that is very low in algorithmic information. At left is the input
that is very low in algorithmic information. At left is the input ![]() and at right is the output
and at right is the output ![]() of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the
of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the ![]() -th RGB value of Signature of the Id is the sum of the first
-th RGB value of Signature of the Id is the sum of the first ![]() RGB values of Fuji Affects the Weather.
RGB values of Fuji Affects the Weather.
What is most remarkable about the increase in “meaning,” i.e., algorithmic specified complexity, is that there actually is loss of information in the data processing. The loss is easy to recognize if you understand that RGB values are 8-bit quantities, and that the sum of two of them is generally a 9-bit quantity, e.g.,
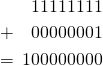
The program ![]() discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image
discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image ![]() from the output image
from the output image ![]() you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
An important detail, which I cannot suppress any longer, is that the algorithmic specified complexity is calculated with respect to binary data called the context. In the calculations above, I have taken the context to be the digital image Fuji. That is, a copy of Fuji has 13 megabits of algorithmic specified complexity in the context of Fuji, and an algorithmically simple corruption of Fuji has 24 megabits of algorithmic specified complexity in the context of Fuji. As in Evo-Info 2, I have used the methods of Ewert, Dembski, and Marks, “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” (2015). My work is recorded in a computational notebook that I will share with you in Evo-Info 5. In the meantime, any programmer who knows how to use an image-processing library can easily replicate my results. (Steps: Convert fuji.png to RGB format; save the cumulative sum of the RGB values, taken in row-major order, as signature.png; then subtract 0.5 Mb from the sizes of fuji.png and signature.png.)
As for the definition of algorithmic specified complexity, it is easiest to understand when expressed as a log-ratio of probabilities,
![]()
where ![]() and
and ![]() are binary strings (finite sequences of 0s and 1s), and
are binary strings (finite sequences of 0s and 1s), and ![]() and
and ![]() are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above,
are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above, ![]() is the probability that a randomly selected computer program converts the context
is the probability that a randomly selected computer program converts the context ![]() into the image
into the image ![]() and
and ![]() is the probability that image
is the probability that image ![]() is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of
is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of ![]() arising by an algorithmic process that depends on the context, and of
arising by an algorithmic process that depends on the context, and of ![]() arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that
arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() and as an alternative hypothesis the proposition that
and as an alternative hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of
then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of ![]() The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level
The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level ![]() when
when ![]()
What we should make of the high algorithmic specified complexity of the images above is that they both are more likely to derive from the context than to arise in the default image-generating process. Again, Fuji is just a copy of the context, and Signature is an algorithmically simple corruption of the context. The probability of randomly selecting a program that cumulatively sums the RGB values of the context is much greater than the probability of generating the image Signature directly, i.e., without use of the context. So we confidently reject the null hypothesis that Signature arose directly in favor of the alternative hypothesis that Signature derives from the context.
This embarrassment of Marks et al. is ultimately their own doing, not mine. It is they who buried the true story of Dembski’s (2005) redevelopment of specified complexity in terms of statistical hypothesis testing, and replaced it with a fanciful account of specified complexity as a measure of meaningful information. It is they who neglected to report that their theorem has nothing to do with meaning, and everything to do with hypothesis testing. It is they who sought out examples to support, rather than to refute, their claims about meaningful information.
Algorithmic specified complexity versus algorithmic mutual information
This section assumes familiarity with the basics of algorithmic information theory.
Objective. Reduce the difference in the expressions of algorithmic specified complexity and algorithmic mutual information, and provide some insight into the relation of the former, which is unfamiliar, to the latter, which is well understood.
Here are the definitions of algorithmic specified complexity (ASC) and algorithmic mutual information (AMI):
![]()
where ![]() is a distribution of probability over the set
is a distribution of probability over the set ![]() of binary strings,
of binary strings, ![]() and
and ![]() are binary strings, and binary string
are binary strings, and binary string ![]() is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity
is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity ![]() and the conditional algorithmic complexity
and the conditional algorithmic complexity ![]() are defined, outputting
are defined, outputting ![]() The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of
The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of ![]() in the context of
in the context of ![]()
The law of conservation (nongrowth) of algorithmic mutual information is:
![]()
for all binary strings ![]() and
and ![]() and for all computable [ETA 12/12/2019: total] functions
and for all computable [ETA 12/12/2019: total] functions ![]() on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability
on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability ![]() where
where ![]() is the empty string, and let
is the empty string, and let ![]() be positive for all nonempty binary strings
be positive for all nonempty binary strings ![]() Also let
Also let ![]() for all binary strings
for all binary strings ![]() Then for all nonempty binary strings
Then for all nonempty binary strings ![]() and for all binary strings
and for all binary strings ![]()
![]()
because
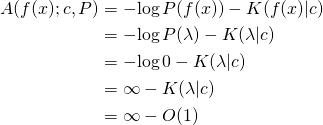
is infinite and ![]() is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that
is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that ![]() is finite for all binary strings
is finite for all binary strings ![]() and
and ![]() I have added a line at the end of the equation to indicate that
I have added a line at the end of the equation to indicate that ![]() is not only finite, but also constant.] Note that this argument can be modified by setting
is not only finite, but also constant.] Note that this argument can be modified by setting ![]() to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing
to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing ![]() can be made arbitrarily large, though not infinite.
can be made arbitrarily large, though not infinite.
There’s a simple way to deal with the different subexpressions ![]() and
and ![]() in the definitions of ASC and AMI, and that is to restrict our attention to the case of
in the definitions of ASC and AMI, and that is to restrict our attention to the case of ![]() in which the context is a shortest program outputting
in which the context is a shortest program outputting ![]()
![]()
This is not an onerous restriction, because there is for every string ![]() a shortest program
a shortest program ![]() that outputs
that outputs ![]() In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as
In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as ![]() We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
![]()
However, the older definition comes with some disadvantages, and I don’t see a significant advantage in using it. Perhaps you will see something that I have not.
The difference in algorithmic mutual information and algorithmic specified complexity,
![]()
has no lower bound, because ![]() is non-negative for all
is non-negative for all ![]() and
and ![]() is negatively infinite for all
is negatively infinite for all ![]() such that
such that ![]() is zero. It is helpful, in the following, to keep in mind the possibility that
is zero. It is helpful, in the following, to keep in mind the possibility that ![]() for a string
for a string ![]() with very high algorithmic complexity, and that
with very high algorithmic complexity, and that ![]() for all strings
for all strings ![]() Then the absolute difference in
Then the absolute difference in ![]() and
and ![]() [added 11/11/2019: the latter expression should be
[added 11/11/2019: the latter expression should be ![]() ] is infinite for all
] is infinite for all ![]() and very large, though finite, for
and very large, though finite, for ![]() There is no limit on the difference for
There is no limit on the difference for ![]() Were Marks et al. to add a requirement that
Were Marks et al. to add a requirement that ![]() be positive for all
be positive for all ![]() we still would be able, with an appropriate definition of
we still would be able, with an appropriate definition of ![]() to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all
to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all ![]()
The remaining difference in the expressions of ASC and AMI is in the terms ![]() and
and ![]() The easy way to reduce the difference is to convert the algorithmic complexity
The easy way to reduce the difference is to convert the algorithmic complexity ![]() into an expression of log-improbability,
into an expression of log-improbability, ![]() where
where
![]()
for all binary strings ![]() An elementary result of algorithmic information theory is that the probability function
An elementary result of algorithmic information theory is that the probability function ![]() satisfies the definition of a semimeasure, meaning that
satisfies the definition of a semimeasure, meaning that ![]() In fact,
In fact, ![]() is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
![]()
that ![]() is a measure, and that
is a measure, and that ![]() is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made
is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made ![]() a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
This does nothing but to establish clearly a sense in which algorithmic specified complexity is formally similar to algorithmic mutual information. As explained above, there can be arbitrarily large differences in the two quantities. However, if we consider averages of the quantities over all strings ![]() holding
holding ![]() constant, then we obtain an interesting result. Let random variable
constant, then we obtain an interesting result. Let random variable ![]() take values in
take values in ![]() with probability distribution
with probability distribution ![]() Then the expected difference of AMI and ASC is
Then the expected difference of AMI and ASC is
![Rendered by QuickLaTeX.com \begin{align*} E[I(X : c) - A(X; c^*\!, P)] &= E[K(X) + \log P(X)] \\ &= E[K(X)] - E[-\!\log P(X)] \\ &= E[K(X)] - H(P). \end{align*}](http://theskepticalzone.com/wp/wp-content/ql-cache/quicklatex.com-318f3c5b560e1b1e12090c6f7bfdfa71_l3.png)
Introducing a requirement that function ![]() be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
![]()
Note that the algorithmic complexity of computable probability distribution ![]() is the length of the shortest program that, on input of binary string
is the length of the shortest program that, on input of binary string ![]() and number
and number ![]() (i.e., a binary string interpreted as a non-negative integer), outputs
(i.e., a binary string interpreted as a non-negative integer), outputs ![]() with
with ![]() bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
![]()
How much the expected value of the AMI may exceed the expected value of the ASC depends on the length of the shortest program for computing ![]()
[Edit 10/30/2019: In the preceding box, there were three instances of ![]() that should have been
that should have been ![]() ] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If
] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If ![]() is computable, then for all binary strings
is computable, then for all binary strings ![]() and
and ![]()
(MDL) 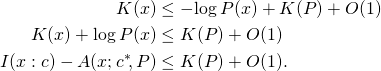
Replacing string ![]() in this inequality with a string-valued random variable
in this inequality with a string-valued random variable ![]() as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
Finally, we express ![]() in terms of the universal conditional semimeasure,
in terms of the universal conditional semimeasure,
![]()
Now ![]() and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that
and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that ![]()
![]()
where ![]() is a distribution of probability over the binary strings
is a distribution of probability over the binary strings ![]() and
and ![]() is the universal conditional semimeasure.
is the universal conditional semimeasure.
An old proof that high ASC is rare
Marks et al. have fostered a great deal of confusion, citing Dembski’s earlier writings containing the term specified complexity — most notably, No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002) — as though algorithmic specified complexity originated in them. The fact of the matter is that Dembski radically changed his approach, but not the term specified complexity, in “Specification: The Pattern that Signifies Intelligence” (2005). Algorithmic specified complexity derives from the 2005 paper, not Dembski’s earlier work. As it happens, the paper has received quite a bit of attention in The Skeptical Zone. See, especially, Elizabeth Liddle’s “The eleP(T|H)ant in the room” (2013).
Marks et al. furthermore have neglected to mention that Dembski developed the 2005 precursor (more general form) of algorithmic specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. Amusingly, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then or equal to
bits of ASC is less then or equal to ![]() ” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
According to the abstract of Milosavljević’s article:
We explore applicability of algorithmic mutual information as a tool for discovering dependencies in biology. In order to determine significance of discovered dependencies, we extend the newly proposed algorithmic significance method. The main theorem of the extended method states that
bits of algorithmic mutual information imply dependency at the significance level
However, most of the argument — particularly, Lemma 1 and Theorem 1 — applies more generally. It in fact applies to algorithmic specified complexity, which, as we have seen, is defined quite similarly to algorithmic mutual information.
Let
and
be probability distributions over sequences (or any other kinds of objects from a countable domain) that correspond to the null and alternative hypotheses respectively; by
and
we denote the probabilities assigned to a sequence
by the respective distributions.
[…]
We now define the alternative hypothesis
in terms of encoding length. Let
denote a decoding algorithm [our universal prefix machine] that can reconstruct the target
[our
] based on its encoding relative to the source
[our context
]. By
[our
] we denote the length of the encoding [for us, this is the length of a shortest program that outputs
on input of
]. We make the standard assumption that encodings are prefix-free, i.e., that none of the encodings represented in binary is a prefix of another (for a detailed discussion of the prefix-free property, see Cover & Thomas, 1991; Li & Vitányi, 1993). We expect that the targets that are similar to the source will have short encodings. The following theorem states that a target
is unlikely to have an encoding much shorter than
THEOREM 1 For any distribution of probabilities
decoding algorithm
and source
Here is a specialization of Theorem 1 within the framework of this post: Let ![]() be a random variable with distribution
be a random variable with distribution ![]() of probability over the set
of probability over the set ![]() of binary strings. Let context
of binary strings. Let context ![]() be a binary string. Then the probability of algorithmic specified complexity
be a binary string. Then the probability of algorithmic specified complexity ![]() is at most
is at most ![]() i.e.,
i.e.,
![]()
For a simpler formulation and derivation, along with a snarky translation of the result into IDdish, see my post “Deobfuscating a Theorem of Ewert, Marks, and Dembski” at Bounded Science.
I emphasize that Milosavljević does not narrow his focus to algorithmic mutual information until Theorem 2. The reason that Theorem 1 applies to algorithmic specified complexity is not that ASC is essentially the same as algorithm mutual information — we established above that it is not — but instead that the theorem is quite general. Indeed, Theorem 1 does not apply directly to the algorithmic mutual information
![]()
because ![]() is a semimeasure, not a measure like
is a semimeasure, not a measure like ![]() Theorem 2 tacitly normalizes the probabilities of the semimeasure
Theorem 2 tacitly normalizes the probabilities of the semimeasure ![]() producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of
producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of ![]() stated in the abstract, which is different from the bound of
stated in the abstract, which is different from the bound of ![]() for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
Conclusion
In 2005, William Dembski made a radical change in what he called specified complexity, and developed the precursor of algorithmic specified complexity. He presented the “new and improved” specified complexity in terms of statistical hypothesis testing. That much of what he did made good sense. There are no formally established properties of algorithmic specified complexity that justify regarding it as a measure of meaningful information. The one theorem that Marks et al. have published is actually a special case of a 1995 result applied to hypothesis testing. In my own exploration of the properties of algorithmic specified complexity, I’ve seen nothing at all to suggest that it is reasonably regarded as a measure of meaning. Marks et al. have attached “meaning” rhetoric to some example applications of algorithmic specific complexity, but have said nothing about counterexamples, which are quite easy to find. In Evo-Info 5, I will explain how to use the methods of “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” to measure large quantities of “meaningful information” in nonsense images derived from the context.
The Series
Evo-Info review: Do not buy the book until…
Evo-Info 1: Engineering analysis construed as metaphysics
Evo-Info 2: Teaser for algorithmic specified complexity
Evo-Info sidebar: Conservation of performance in search
Evo-Info 3: Evolution is not search
Evo-Info 4: Non-conservation of algorithmic specified complexity
Evo-Info 4 addendum
[Some minor typographical errors in the original post have been corrected.]



Ok that was a fast light read 🙂
Yes, I agree that there is a socio-political element to the IDM. It’s a tangent from the purpose of the article, still I’m just curious why you don’t capitalise ‘Intelligent Design,’ choosing instead use the non-capitalised version?
Two main reasons for capitalisation:
1) The term ‘Intelligent Design’ becomes a proper noun when combined with ‘Movement.’
or
2) Because everyone knows that ID ‘theorists’ almost all mean the Abrahamic God of Scripture when they refer to an Intelligent Designer & that the Intelligent Design itself is ‘non-naturalistic’.
Does this change your mind or help show at least why there is contention over the difference between capitalised & non-capitalised uses of ‘Intelligent Design/intelligent design’ in the literature? It is not unlike why the term BioLogos specifically included a capitalised ‘L’ in the mind of Francis Collins.
Nice that you’re aiming to identify & spread ‘meaningful information’ to so many people, Tom.
Interesting Gregory…
Is IDiot rather than idiot an attempt to spread more meaningful information?
Thanks for this,Tom. Appreciate the hard work (though can’t comment usefully on the math). Could I suggest we (fellow members) don’t clutter the thread with knee-jerk off-topic comments. It’s not a rule, more of a guideline…
There’s nothing deep in the math. The derivations are actually quite simple. But figuring out which simple derivations to do, when there is no one showing you the way to go, is hard work. It’s very different from solving a structured problem that a math teacher has set before you.
You actually need not know anything about algorithmic information theory to check my proof of unbounded growth in algorithmic specified complexity (ASC). What I’ve done is to write out the definition of ASC, and then to derive a particular consequence of it. You don’t need to grasp the full significance of the definition in order to see that each of the steps in the derivation is justified. The justifications of the steps are all common mathematical knowledge. If this is not your accustomed mode of thinking, then it will seem arcane to you. But the reality is that I have, proceeding with a succession of simple steps, rendered my conclusion utterly unmysterious.
Eric Holloway should understand that he’s being tested. I’ve illustrated how formal arguments actually go. If he responds with a mathematicalistic flurry of technical terms and symbols, rather than a sequence of simple steps from antecedents to consequents (each with a clear justification), then he will have confirmed that he is the crackpot that he’s seemed thus far to be. In all sincerity, I’d rather that he show himself to be a worthy adversary.
I am hoping Eric is watching and can confirm this. It might be nice to see what people agree on before moving off into any areas of disagreement.
Tom: Thanks for this wonderful introduction to Algorithmic Info and its uses and misuses.
I look forward to studying and learning from it.
I’m not aware of any measure of “information” that is a measure of meaningful information or that can be reasonably regarded as a measure of meaning. Maybe these ID guys can come up with one. 😉
I’d say that their odds of success would be considerably greater if they set out to do particularly that, rather than to weave a new tale around Dembski’s old work.
It is bizarre that Marks et al. silently abandoned the part of Dembski (2005) that was straightforward and coherent. Dembski indeed did reformulate specified complexity as a test statistic. (Whether you can reject a null hypothesis about nature in favor of an alternative metaphysical stance, teleology, is a separate question.) So Marks et al. should have told us why they thought specified complexity did not make sense as a test statistic, and did make sense as a measure of meaning.
I want to emphasize that I did not merely bash the notion that ASC is a measure of meaning by displaying an embarrassing counterexample. I made sense of the high ASC of Signature of the Id in terms of hypothesis testing. So I lent some credence to Dembski’s 2005 claims (though not to his notion that rejection of the null was a design inference: corruption of an existing image by an extremely simple process is not intelligent design).
This is not true. You need to know that is finite for all binary strings
is finite for all binary strings  and
and  This is a basic result in algorithmic information theory, which I said was required to read the formal section, but is not common mathematical knowledge.
This is a basic result in algorithmic information theory, which I said was required to read the formal section, but is not common mathematical knowledge.
Mung,
Yes, I agree with Dr. English that using Mc(x) = 2^-K(x|C) makes it easier to reason mathematically about ASC. If anyone has looked through my OP they’d see I switch between the two forms.
I see no problem with Tom English’s mathematics in this post. It has excellent presentation, and a couple interesting results. I also don’t see it as particularly controversial that there can be an unbounded difference between the chance hypothesis and some other probability distribution, but I’m probably missing something important here as I am wont to do.
When I mentioned conservation of ASC in the other thread, what I had in mind is there is non positive expected ASC under the chance hypothesis, because taking the expectation is the negative Kullback-Liebler divergence, which is always non positive.
The ASC conservation law is somewhat interesting because Dembski’s original CSI can form a harmonic sequence with his variant of specification, so the conservation law doesn’t hold. We can easily construct scenarios where the expected CSI is arbitrarily large since the harmonic sequence diverges. This violates the true positive guarantee that CSI is supposed to provide. However, we can either normalize the harmonic series for a finite set of events, or we can just switch to using ASC, which does not have this flaw.
Conservation of ASC is also slightly interesting because conservation of ASC is of the same form as Levin’s random variant of the conservation law (in case someone actually read through the math of my OP). Eventually I’ll have a post tying these things together, or that Bio-C paper will be finally get submitted and some day accepted…
Thanks.
Yeah, I worried that I was not being explicit enough with the boxed statement:
There is no upper bound on the increase of algorithmic specified complexity due to data processing.
It means:
Algorithmic specified complexity is not conserved in the sense that algorithmic mutual information is conserved.
For algorithmic mutual information,
for all binary strings and
and  and for all computable functions
and for all computable functions  on the binary strings.
on the binary strings.
But for algorithmic specified complexity, there exist binary strings and
and  probability distribution
probability distribution  over the binary strings, and computable function
over the binary strings, and computable function  on the binary strings such that
on the binary strings such that
So there’s no bound at all on the increase in algorithmic specified complexity due to the processing of data
of data  This is pretty much the opposite of conservation.
This is pretty much the opposite of conservation.
It would be helpful if you were to write out formally what you mean. I suppose you’re saying that
where is the Kullback-Leibler divergence of
is the Kullback-Leibler divergence of  from
from  However, the second equality is incorrect, because
However, the second equality is incorrect, because  is a semimeasure: the probabilities do not sum to 1 as required by the definition of the Kullback-Leibler divergence.
is a semimeasure: the probabilities do not sum to 1 as required by the definition of the Kullback-Leibler divergence.
Why would you call this conservation of information? It is not conservation of information in any sense like that of Levin.
Edit: Was missing a factor in the first summation.
factor in the first summation.
Algorithmic specified complexity appears nowhere in the write-up that you link to from your OP.
Algorithmic specified complexity most definitely does appear in my OP, above. I’ve provided the formalism for dealing with the random case. So go ahead and show us the derivation. The fact that you have a paper forthcoming does not stop you from doing that.
Tom English,
First of all, I appreciate you have spent a lot of effort to spell out your refutation technically. This is great, and much more than I usually see from ID critics, which I why I pay attention to your work. Even if I disagree, I usually learn something.
Now, I’ll repeat here the AIT conservation law you are working with:
I(f(x):y) <= I(x:y) + k(f) + O(1).
Something to note is this is not the law I am referring to, if you'll check the linked article in my OP. The key point is the law above does not say anything about the relation of f and y, but Levin's proof takes this into account and shows when we select f randomly the expected gain is non-positive. Additionally, I only refer to CSI in the OP script as a motivating factor for my proof. ASC/CSI do not appear at all in the linked proof, so your ASC non conservation law does not apply to my proof.
I do claim in scattered posts and comments that ASC/CSI are forms of mutual information and thus conservation laws apply to them, related to my bigger claim that Dembski's work is well supported by standard information theory. As previously mentioned, this is more an intuition than a formally demonstrated claim. I will be working on a formal writeup in the near future, and will address how it relates to your work here.
I found it remarkable there appear to be a number of concepts in information theory
– mutual information
– data processing inequality
– Levin's law
– Kullback-Liebler divergence
– Kolmogorov minimal sufficient statistic
– algorithmic universal probability
– halting oracles
+ a few others
that intuitively seem easy to connect to Dembski's formal work, and consequently left me questioning why information theory experts like yourself and Dr. Shallit do not make the connections that seem so obvious to me, or even address them. I have seen you offhand remark on the similarity between the data processing inequality and Dembski's conservation of information in a UD comment under your pseudoname "Erasmus Wiffball" and you also remarked on Levin's work, so you appear to notice some of the similarity that I see.
This is why it does not appear the controversy that you &co. raise in regards to Dembski's work is well founded. It at least appears you all are selectively reporting from your information theory expertise and for some reason purposefully ignoring points in Dembski's favor. Perhaps I am mistaken, but I definitely do not detect a tone of charity in your treatment of Dembski's work, nor from any of the other critics I have interacted with. This in itself seems odd and uncollegial. There is an overriding and continuous insinuation of ill intent on the part of Dembski, whereas a charitable treatment would start with an innocent until proven guilty position. A truly charitable treatment would be to make the best case possible for Dembski's work, and then dismantle that position. I have never seen this happen, except to set up what look like clear strawmen.
Given this growing perception on my part as I've studied information theory, you might then understand why I experience the opposite reaction: that Dembski must certainly be on to something to be treated in such an unprofessional manner with little basis by his colleagues. I saw this at the beginning of my research into ID, and the perception has not lessened over the decade plus that I have spent in fairly unbiased (my opinion) studies on the topic. I would be quite happy if yourself or some other critic fairly put ID away, and I'd eat crow and go on my merry way. Yet I have never seen fair treatment of ID. Your work gets the closest that I've seen.
My time over at Peaceful Science certainly strengthen my perception of baseless accusation on the part of the critics. So, I hope that our interactions on this forum can serve to reverse the perception I've developed over the years.
And, there is always the possibility I’m a crackpot 😀
I see at least two types of criticisms: those based on math and those based on biology.
I hope you will consider the biological requirements in your next posts on the “Breaking the law of information non growth” thread. Joe has laid some out near the end of the thread. I think that unless you and the biologists agree on what needs to be explained, there is no point in discussion of the math of information theory.
Scientists and philosophers are people; it’s common to see emotions intrude in any controversy where the sides have long standing disagreements because eg they don’t agree on the base requirements to be explained or the criteria for “best” when making an inference to best explanation.
In this case, I see an added concern that would irk scientists: ID theory can be read as a type of rationalism. That is, it claims to draw conclusions about science based on a priori, mathematical reasons, and is seen as ignoring or unreasonably discounting the empirical work of science and the resulting IBE underlying biological evolution.
Bruce has already made the point but I’ll reiterate. The reason Dembski’s work has been ignored by biologists is simply that it has no relevance to biology. Dembski’s model does not represent biological observation.
This^
Alan Fox,
Why do you think it has no relevance to biology?
colewd,
Did you miss the bit where I said Dembski’s model does not match biological reality?
Bill, is this a fair representation of Dembski’s position:
In his 2005 paper, Specification: the Pattern that Signifies Intelligence, Dembski makes a bold claim: that there is an identifiable property of certain patterns that “Signifies Intelligence”. Dembski spends the major part of his paper on making three points:
1. He takes us on a rather painful walk-through Fisherian null hypothesis testing, which generates the probability (the “p value”) that we would observe our data were the null to be true, and allows us to “reject the null” if our data fall in the tails of the probability distribution where the p value falls below our “alpha” criterion: the “rejection region”.
2. He argues that if we set the “alpha” criterion at which we reject a Fisherian null as 1/[the number of possible events in the history of the universe], no way jose will we ever see the observed pattern under that null. tbh I’d be perfectly happy to reject a non-Design null at a much more lenient alpha that that.
3. He defines a pattern as being Specified if it is both
a. One of a very large number of patterns that could be made from the same
elements (Shannon Complexity)
b. One of a very small subset of those patterns that can be defined as, or more simply than the pattern in question (Kolmogorov compressibility)
He then argues that if a pattern is one of a very small specifiable subset of patterns that could be produced under some non-Design null hypothesis, and that subset is less than 1/[the number of possible events in the history of the universe] of the whole set, it has CSI and we must conclude Design.
Dr Elizabeth Liddle
This makes sense when it comes to biology. It’s hard to have a discussion if no one agrees on what needs to be discussed. I think Felsenstein’s model can be a good starting point.
However, the information theory is prior to the agreement on the biological details. The information theory shows there are certain characteristics that cannot have randomness + Turing machine explanations. If we first establish what those characteristics are, then we can look into the biological world to see if they show up.
And per your point about rationalism, I get it that we don’t want to try to force the world into our preconceived notions. But, thought experiments from first principles are very important for advancing science. For example, that is how Einstein came up with his theory of relativity, and Bell came up with his proof of non locality by reasoning from first principles. So, we shouldn’t force the data to fit our model, but on the other hand there is the saying “there is nothing so practical as good theory.”
All that to say, the information theory math is quite important to think through carefully independently from a particular application, say in biology or regarding the structure of the universe. Thus, we shouldn’t dismiss Dembski’s work just because we disagree with one way it is applied. The theory may be sound even if the application is wrong, and understanding the theory better helps us to know whether and where it can be applied.
Alan Fox,
The big picture purpose of Dembski’s work is to show we can legitimately identify hypotheses after seeing the data. Within the Fisherian framework all hypotheses must be established before seeing the data. This is a very practical result, especially within my area of interest of machine learning, which is traditionally cast in the Fisherian framework.
It is very closely related to algorithmic information theory’s motivation. Shannon information does not allow us to distinguish between these two strings:
1. 00000000000000000000
2. 10100010101101111001
According to Shannon information both strings are equally likely. So, if we saw 100 coin flips turn up heads, we’d have no basis for suspecting the coin is not fair. On the other hand, Kolmogorov came up with his notion of algorithmic information theory (AIT) to allow us to say that string #1 is much more unlikely than string #2, because the latter is a typical random bitstring. Thus, if we saw 100 heads, we have good reason to believe the coin is not fair.
Dembski explanatory filter/CSI has the same motivation as Kolmogorov’s AIT, but he is providing a more general account, and providing the additional step that allows us to go from identifying an atypical sequence to inferring the probable cause.
We build castles in the sky. The information theory argument is all about those castles in the sky. The information theory argument is all about how many angels can dance on the head of a pin.
It is all human constructed make-believe — as is all of mathematics (and I say that as a mathematician).
Unless, of course, we have a clear mapping from reality to those abstract models. And when your argument is about biology, you need a clear mapping from biological reality to your abstract models. And that is what is missing.
No, the information argument is not prior to the biological details. Rather, it is orthogonal to the biological details. And it is completely irrelevant to the biology, unless you first build the connections. And that’s what the ID folk have consistently failed to do.
Neil Rickert,
I would draw the analogy with Bell’s theorem, where he came up with his test for non locality based on mathematical first principles. Only now, 50+ years after he came up with the theory do we have loophole free empirical verification of his idea. Theory preceded the application by many decades.
EricMH,
Thanks for the reply Eric.
I may be misunderstanding Dembski’s argument-
but he seems to be multiplying rare events (and there’s also an issue WRT proteins from DNA sequences that involves an assumption on rarity) rather than looking at the reality of each generation in a population starting from the scratch position of being alive and trying to survive and procreate in their niche environment resulting in successive viable modifications to the genome.
Fair enough.
When can we expect to see the ID people stop their nonsense about “teach the controversy”, and instead start on that 50 year program of coming up with empirical support for their claims?
If the ID people want to change the world, that’s how to do it.
You are certain that Dembski’s CSI argument shows that humans cannot have evolved without intelligent guidance, but you are a bit hazy on which characteristics actually show that?
How does that work?
The word “characteristics” is not helpful, I think. It has overtones implying something of reality, at least to me. OTOH, the only consequences one can draw from uninterpreted math are simply further math. From A, B follows, if this proof is valid. That’s it.
Nothing about the world itself can be concluded.
Thought experiments are fine. The thing is, we only remember the ones which which were confirmed by subsequent science. Einstein related his thought experiment to science, eg GR started with his happiest thought but was not accepted until predictions about mercury’s orbit or how much starlight bends were made and confirmed.
My point being is that it was not science until the theory was interpreted for testing.
Bell’s theorem started with existing science, not math. It was a matter of using the math of consensus QM to predict certain consequences for our interpretations of QM.
Bell’s theorem is not a good analogy to use for ID because Bell started with the science whereas ID starts with the math.
ETA: Probably more historically accurate to say Einstein started with the science in his EPR argument and then Bell built on that base. See Maudlin’s What Bell Did.
@Neil, I believe ID is currently working on both the science and the PR at the same time. For example, see Dr. Ewert’s excellent work. I would not have found out about ID if not for their PR work, so I think both are valuable. Of course, the PR should not be focussed on at the expense of the science, which has happened to some extent in my opinion.
@Corneel, I have my own opinions as to what the characteristics are, but I cannot make my case well enough in biological terminology to be of value in this forum.
@BruceS, from my perception the analogy is pretty close with Bell’s theorem. Dembski’s work was motivated by the scientific observation by non ID related individuals that biological organisms exhibit specified complexity, and his own mathematical experience in randomness testing.
Bell took the scientific motivation, but then went to mathematical first principles to show that if the two particles are independent then there is a logically necessary pattern (for lack of a better word) they must exhibit. Thus, if empirical data shows particles do not have this pattern, then they must be dependent.
This looks very similar to what you are calling rationalism in ID. I cannot help but think this is essentially the same thing that Dembski has done. He had motivation from scientific observation, and then went to mathematical first principles to derive his theory.
There would be value, Eric, I’m sure. I’m convinced the central issue is maps and territory – how well you are mapping reality.
What do you suggest Dembski observed?
@ Eric:
I notice you
This is a good question. 😉
It’s the topic of my next article, so stay tuned!
This is the end of my engagement here. It has been a goodish experience, so I will venture back when I have more content to discuss.
Don’t tell me. You’ve got a hunch.
Looking forward to seeing the math hooked up to a model of Joe’s bitstring creatures. Hopefully that will give me some more intuition how Dembski’s law of conservation of information is supposed to work.
In Bell, Bell: “independent” had precise statistical derivation which he then interpreted into QM so it could be tested. EPR was motivated by QM predictions of behavior of spacelike separated quanta (and Einstein’s refusal to accept a non-local QM as complete).
“organisms exhibited specified information.” I don’t see any science in that. Just Demski’s personal view and then a math formula he defined to formalize that view. To call it ‘science’ requires relating it to some some existing scientific research program.
Of course, you may say that ID qualifies as the science Dembski started from.
On that, I suspect we would be stalemated, and unless we went through a lot of philosophical to-and-fro about demarcation of science. But we’re already OT, so over to you for last word on this; I’ll stop. (Although I see you from a later post have already moved on….)
I do look forward to how the biology goes in your thread plus learning some neat math from Tom in this one.
Great work Tom. Thanks for positing this. We linking to this at Peaceful Science. I hope we can discuss it sometime after the final posts are up. https://discourse.peacefulscience.org/t/tom-english-review-of-evolutionary-informatics-marks-et-al/3121
I’m sorry to disappoint you Eric but the freedom-of-choice loophole can never be completely shut in the experimental tests of Bell’s theorem…
All one can do is significantly close each loophole as with each assumption needed for the experiment a door gets open to at least one loophole… The latest experiment I’m aware of pushed back determinism to over a billion years…
But that’s not good enough for those who always find a stick (superdeterminism) to beat a dog…
Just like Darwin’s boys here you have been dealing with… Even if your math works, as it should, because even my kids know 1+1 never =3,
they already “have a stick to beat the dog”: your math doesn’t apply to biology…
You don’t need me to predict the future for you… You are smart enough to already know that…
ETA: Do you know anything about the category theory that stems from the set theory?
I think you need to bring in more evolutionary militia on the board of directors at PS to attract more people from TSZ…
Jerry Coyne would work well with Dr. Trishittata… They have very similar traits that would help them become the dream Darwinian Gestapo team. Jerry already banned every ID proponent on his blog and all atheists and Darwinists that disagree with him or don’t like the “talking cat”…
This is what happens to people with gargantuan egos and hidden, and yet easy to figure out, agenda… It looks like Ann Gauger and Paul Nelson figured out your agenda… Behe and Axe had known it right from the beginning…
There are a large range of views at PS. One of our selling points, right now, is that we are far more effective at dealing with Trolls than TSZ or Panda’s Thumb. I hope that both these sites get a better system soon, but the current situation is intolerable. It is well known that many trolls plague the forums out there on ID and evolution, and they appear on all sides. At PS we do not tolerate trolling, especially when it disrupts meaningful dialogue.
If anyone who wants to conduct an exchange of high importance (such as between Eric Holloway, Joe Feldstein, and Tom English), we can create a public thread that only they can contribute to. PS is not just about me. If they desire it so, I’m happy to stay out of it entirely, so they can hash things out without interference.
What ever we can do to help, let me know. Peace.
We have a separate thread for discussing moderation issues but I will just say there is no technical problem at TSZ in restricting access. It is something we are reluctant, rather than unable, to do.
swamidass, the ‘x’ button next to people’s name allows them to be ignored. Most people, for example, seem to have a sub-set of commentors on ignore. It works well I think.
It’s useful but to be completely effective one would need to be able to block replies to the people you block and OPs by the people you block.
Very good tip. Thanks!
Understood.
Well, longerish would have been betterish. A proper response to your comments will take some time. I’ve been (happily) tied up with family. I don’t know how much time I’ll have to myself today.
They are still trying to figure out how to deal with me. 😉
Moved a comment to guano.
Thank you!
I’m really sorry that Dr. Swamidass can’t read guano… I think he should appeal to his god for help…
Maybe you can explain how it is possible in your fair treatment of contributors at PS that Dr. Trashitata gets flagged by the “community” (joke) and never gets banned…Why would you let an atheist to trash Jesus your apparent savior?
What would Jesus say if he were to comment here?