Subjects: Evolutionary computation. Information technology–Mathematics.
The greatest story ever told by activists in the intelligent design (ID) socio-political movement was that William Dembski had proved the Law of Conservation of Information, where the information was of a kind called specified complexity. The fact of the matter is that Dembski did not supply a proof, but instead sketched an ostensible proof, in No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002). He did not go on to publish the proof elsewhere, and the reason is obvious in hindsight: he never had a proof. In “Specification: The Pattern that Signifies Intelligence” (2005), Dembski instead radically altered his definition of specified complexity, and said nothing about conservation. In “Life’s Conservation Law: Why Darwinian Evolution Cannot Create Biological Information” (2010; preprint 2008), Dembski and Marks attached the term Law of Conservation of Information to claims about a newly defined quantity, active information, and gave no indication that Dembski had used the term previously. In Introduction to Evolutionary Informatics, Marks, Dembski, and Ewert address specified complexity only in an isolated chapter, “Measuring Meaning: Algorithmic Specified Complexity,” and do not claim that it is conserved. From the vantage of 2018, it is plain to see that Dembski erred in his claims about conservation of specified complexity, and later neglected to explain that he had abandoned them.
Algorithmic specified complexity is a special form of specified complexity as Dembski defined it in 2005, not as he defined it in earlier years. Yet Marks et al. have cited only Dembski’s earlier publications. They perhaps do not care to draw attention to the fact that Dembski developed his “new and improved” specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. That’s obviously quite different from their current presentation of algorithmic specified complexity as a measure of meaning. Ironically, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then [sic] or equal to
bits of ASC is less then [sic] or equal to ![]() ” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
Lately, a third-wave ID proponent by the name of Eric Holloway has spewed mathematicalistic nonsense about the relationship of specified complexity to algorithmic mutual information. [Note: Eric has since joined us in The Skeptical Zone, and I sincerely hope to see that he responds to challenges by making better sense than he has previously.] In particular, he has claimed that a conservation law for the latter applies to the former. Given his confidence in himself, and the arcaneness of the subject matter, most people will find it hard to rule out the possibility that he has found a conservation law for specified complexity. My response, recorded in the next section of this post, is to do some mathematical investigation of how algorithmic specified complexity relates to algorithmic mutual information. It turns out that a demonstration of non-conservation serves also as an illustration of the senselessness of regarding algorithmic specified complexity as a measure of meaning.
Let’s begin by relating some of the main ideas to pictures. The most basic notion of nongrowth of algorithmic information is that if you input data ![]() to computer program
to computer program ![]() then the amount of algorithmic information in the output data
then the amount of algorithmic information in the output data ![]() is no greater than the amounts of algorithmic information in input data
is no greater than the amounts of algorithmic information in input data ![]() and program
and program ![]() added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image
added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image ![]() by a program
by a program ![]() that is very low in algorithmic information. At left is the input
that is very low in algorithmic information. At left is the input ![]() and at right is the output
and at right is the output ![]() of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the
of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the ![]() -th RGB value of Signature of the Id is the sum of the first
-th RGB value of Signature of the Id is the sum of the first ![]() RGB values of Fuji Affects the Weather.
RGB values of Fuji Affects the Weather.
What is most remarkable about the increase in “meaning,” i.e., algorithmic specified complexity, is that there actually is loss of information in the data processing. The loss is easy to recognize if you understand that RGB values are 8-bit quantities, and that the sum of two of them is generally a 9-bit quantity, e.g.,
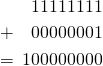
The program ![]() discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image
discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image ![]() from the output image
from the output image ![]() you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
An important detail, which I cannot suppress any longer, is that the algorithmic specified complexity is calculated with respect to binary data called the context. In the calculations above, I have taken the context to be the digital image Fuji. That is, a copy of Fuji has 13 megabits of algorithmic specified complexity in the context of Fuji, and an algorithmically simple corruption of Fuji has 24 megabits of algorithmic specified complexity in the context of Fuji. As in Evo-Info 2, I have used the methods of Ewert, Dembski, and Marks, “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” (2015). My work is recorded in a computational notebook that I will share with you in Evo-Info 5. In the meantime, any programmer who knows how to use an image-processing library can easily replicate my results. (Steps: Convert fuji.png to RGB format; save the cumulative sum of the RGB values, taken in row-major order, as signature.png; then subtract 0.5 Mb from the sizes of fuji.png and signature.png.)
As for the definition of algorithmic specified complexity, it is easiest to understand when expressed as a log-ratio of probabilities,
![]()
where ![]() and
and ![]() are binary strings (finite sequences of 0s and 1s), and
are binary strings (finite sequences of 0s and 1s), and ![]() and
and ![]() are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above,
are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above, ![]() is the probability that a randomly selected computer program converts the context
is the probability that a randomly selected computer program converts the context ![]() into the image
into the image ![]() and
and ![]() is the probability that image
is the probability that image ![]() is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of
is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of ![]() arising by an algorithmic process that depends on the context, and of
arising by an algorithmic process that depends on the context, and of ![]() arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that
arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() and as an alternative hypothesis the proposition that
and as an alternative hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of
then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of ![]() The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level
The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level ![]() when
when ![]()
What we should make of the high algorithmic specified complexity of the images above is that they both are more likely to derive from the context than to arise in the default image-generating process. Again, Fuji is just a copy of the context, and Signature is an algorithmically simple corruption of the context. The probability of randomly selecting a program that cumulatively sums the RGB values of the context is much greater than the probability of generating the image Signature directly, i.e., without use of the context. So we confidently reject the null hypothesis that Signature arose directly in favor of the alternative hypothesis that Signature derives from the context.
This embarrassment of Marks et al. is ultimately their own doing, not mine. It is they who buried the true story of Dembski’s (2005) redevelopment of specified complexity in terms of statistical hypothesis testing, and replaced it with a fanciful account of specified complexity as a measure of meaningful information. It is they who neglected to report that their theorem has nothing to do with meaning, and everything to do with hypothesis testing. It is they who sought out examples to support, rather than to refute, their claims about meaningful information.
Algorithmic specified complexity versus algorithmic mutual information
This section assumes familiarity with the basics of algorithmic information theory.
Objective. Reduce the difference in the expressions of algorithmic specified complexity and algorithmic mutual information, and provide some insight into the relation of the former, which is unfamiliar, to the latter, which is well understood.
Here are the definitions of algorithmic specified complexity (ASC) and algorithmic mutual information (AMI):
![]()
where ![]() is a distribution of probability over the set
is a distribution of probability over the set ![]() of binary strings,
of binary strings, ![]() and
and ![]() are binary strings, and binary string
are binary strings, and binary string ![]() is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity
is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity ![]() and the conditional algorithmic complexity
and the conditional algorithmic complexity ![]() are defined, outputting
are defined, outputting ![]() The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of
The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of ![]() in the context of
in the context of ![]()
The law of conservation (nongrowth) of algorithmic mutual information is:
![]()
for all binary strings ![]() and
and ![]() and for all computable [ETA 12/12/2019: total] functions
and for all computable [ETA 12/12/2019: total] functions ![]() on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability
on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability ![]() where
where ![]() is the empty string, and let
is the empty string, and let ![]() be positive for all nonempty binary strings
be positive for all nonempty binary strings ![]() Also let
Also let ![]() for all binary strings
for all binary strings ![]() Then for all nonempty binary strings
Then for all nonempty binary strings ![]() and for all binary strings
and for all binary strings ![]()
![]()
because
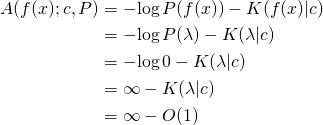
is infinite and ![]() is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that
is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that ![]() is finite for all binary strings
is finite for all binary strings ![]() and
and ![]() I have added a line at the end of the equation to indicate that
I have added a line at the end of the equation to indicate that ![]() is not only finite, but also constant.] Note that this argument can be modified by setting
is not only finite, but also constant.] Note that this argument can be modified by setting ![]() to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing
to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing ![]() can be made arbitrarily large, though not infinite.
can be made arbitrarily large, though not infinite.
There’s a simple way to deal with the different subexpressions ![]() and
and ![]() in the definitions of ASC and AMI, and that is to restrict our attention to the case of
in the definitions of ASC and AMI, and that is to restrict our attention to the case of ![]() in which the context is a shortest program outputting
in which the context is a shortest program outputting ![]()
![]()
This is not an onerous restriction, because there is for every string ![]() a shortest program
a shortest program ![]() that outputs
that outputs ![]() In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as
In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as ![]() We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
![]()
However, the older definition comes with some disadvantages, and I don’t see a significant advantage in using it. Perhaps you will see something that I have not.
The difference in algorithmic mutual information and algorithmic specified complexity,
![]()
has no lower bound, because ![]() is non-negative for all
is non-negative for all ![]() and
and ![]() is negatively infinite for all
is negatively infinite for all ![]() such that
such that ![]() is zero. It is helpful, in the following, to keep in mind the possibility that
is zero. It is helpful, in the following, to keep in mind the possibility that ![]() for a string
for a string ![]() with very high algorithmic complexity, and that
with very high algorithmic complexity, and that ![]() for all strings
for all strings ![]() Then the absolute difference in
Then the absolute difference in ![]() and
and ![]() [added 11/11/2019: the latter expression should be
[added 11/11/2019: the latter expression should be ![]() ] is infinite for all
] is infinite for all ![]() and very large, though finite, for
and very large, though finite, for ![]() There is no limit on the difference for
There is no limit on the difference for ![]() Were Marks et al. to add a requirement that
Were Marks et al. to add a requirement that ![]() be positive for all
be positive for all ![]() we still would be able, with an appropriate definition of
we still would be able, with an appropriate definition of ![]() to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all
to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all ![]()
The remaining difference in the expressions of ASC and AMI is in the terms ![]() and
and ![]() The easy way to reduce the difference is to convert the algorithmic complexity
The easy way to reduce the difference is to convert the algorithmic complexity ![]() into an expression of log-improbability,
into an expression of log-improbability, ![]() where
where
![]()
for all binary strings ![]() An elementary result of algorithmic information theory is that the probability function
An elementary result of algorithmic information theory is that the probability function ![]() satisfies the definition of a semimeasure, meaning that
satisfies the definition of a semimeasure, meaning that ![]() In fact,
In fact, ![]() is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
![]()
that ![]() is a measure, and that
is a measure, and that ![]() is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made
is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made ![]() a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
This does nothing but to establish clearly a sense in which algorithmic specified complexity is formally similar to algorithmic mutual information. As explained above, there can be arbitrarily large differences in the two quantities. However, if we consider averages of the quantities over all strings ![]() holding
holding ![]() constant, then we obtain an interesting result. Let random variable
constant, then we obtain an interesting result. Let random variable ![]() take values in
take values in ![]() with probability distribution
with probability distribution ![]() Then the expected difference of AMI and ASC is
Then the expected difference of AMI and ASC is
![Rendered by QuickLaTeX.com \begin{align*} E[I(X : c) - A(X; c^*\!, P)] &= E[K(X) + \log P(X)] \\ &= E[K(X)] - E[-\!\log P(X)] \\ &= E[K(X)] - H(P). \end{align*}](http://theskepticalzone.com/wp/wp-content/ql-cache/quicklatex.com-318f3c5b560e1b1e12090c6f7bfdfa71_l3.png)
Introducing a requirement that function ![]() be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
![]()
Note that the algorithmic complexity of computable probability distribution ![]() is the length of the shortest program that, on input of binary string
is the length of the shortest program that, on input of binary string ![]() and number
and number ![]() (i.e., a binary string interpreted as a non-negative integer), outputs
(i.e., a binary string interpreted as a non-negative integer), outputs ![]() with
with ![]() bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
![]()
How much the expected value of the AMI may exceed the expected value of the ASC depends on the length of the shortest program for computing ![]()
[Edit 10/30/2019: In the preceding box, there were three instances of ![]() that should have been
that should have been ![]() ] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If
] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If ![]() is computable, then for all binary strings
is computable, then for all binary strings ![]() and
and ![]()
(MDL) 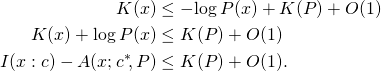
Replacing string ![]() in this inequality with a string-valued random variable
in this inequality with a string-valued random variable ![]() as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
Finally, we express ![]() in terms of the universal conditional semimeasure,
in terms of the universal conditional semimeasure,
![]()
Now ![]() and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that
and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that ![]()
![]()
where ![]() is a distribution of probability over the binary strings
is a distribution of probability over the binary strings ![]() and
and ![]() is the universal conditional semimeasure.
is the universal conditional semimeasure.
An old proof that high ASC is rare
Marks et al. have fostered a great deal of confusion, citing Dembski’s earlier writings containing the term specified complexity — most notably, No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002) — as though algorithmic specified complexity originated in them. The fact of the matter is that Dembski radically changed his approach, but not the term specified complexity, in “Specification: The Pattern that Signifies Intelligence” (2005). Algorithmic specified complexity derives from the 2005 paper, not Dembski’s earlier work. As it happens, the paper has received quite a bit of attention in The Skeptical Zone. See, especially, Elizabeth Liddle’s “The eleP(T|H)ant in the room” (2013).
Marks et al. furthermore have neglected to mention that Dembski developed the 2005 precursor (more general form) of algorithmic specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. Amusingly, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then or equal to
bits of ASC is less then or equal to ![]() ” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
According to the abstract of Milosavljević’s article:
We explore applicability of algorithmic mutual information as a tool for discovering dependencies in biology. In order to determine significance of discovered dependencies, we extend the newly proposed algorithmic significance method. The main theorem of the extended method states that
bits of algorithmic mutual information imply dependency at the significance level
However, most of the argument — particularly, Lemma 1 and Theorem 1 — applies more generally. It in fact applies to algorithmic specified complexity, which, as we have seen, is defined quite similarly to algorithmic mutual information.
Let
and
be probability distributions over sequences (or any other kinds of objects from a countable domain) that correspond to the null and alternative hypotheses respectively; by
and
we denote the probabilities assigned to a sequence
by the respective distributions.
[…]
We now define the alternative hypothesis
in terms of encoding length. Let
denote a decoding algorithm [our universal prefix machine] that can reconstruct the target
[our
] based on its encoding relative to the source
[our context
]. By
[our
] we denote the length of the encoding [for us, this is the length of a shortest program that outputs
on input of
]. We make the standard assumption that encodings are prefix-free, i.e., that none of the encodings represented in binary is a prefix of another (for a detailed discussion of the prefix-free property, see Cover & Thomas, 1991; Li & Vitányi, 1993). We expect that the targets that are similar to the source will have short encodings. The following theorem states that a target
is unlikely to have an encoding much shorter than
THEOREM 1 For any distribution of probabilities
decoding algorithm
and source
Here is a specialization of Theorem 1 within the framework of this post: Let ![]() be a random variable with distribution
be a random variable with distribution ![]() of probability over the set
of probability over the set ![]() of binary strings. Let context
of binary strings. Let context ![]() be a binary string. Then the probability of algorithmic specified complexity
be a binary string. Then the probability of algorithmic specified complexity ![]() is at most
is at most ![]() i.e.,
i.e.,
![]()
For a simpler formulation and derivation, along with a snarky translation of the result into IDdish, see my post “Deobfuscating a Theorem of Ewert, Marks, and Dembski” at Bounded Science.
I emphasize that Milosavljević does not narrow his focus to algorithmic mutual information until Theorem 2. The reason that Theorem 1 applies to algorithmic specified complexity is not that ASC is essentially the same as algorithm mutual information — we established above that it is not — but instead that the theorem is quite general. Indeed, Theorem 1 does not apply directly to the algorithmic mutual information
![]()
because ![]() is a semimeasure, not a measure like
is a semimeasure, not a measure like ![]() Theorem 2 tacitly normalizes the probabilities of the semimeasure
Theorem 2 tacitly normalizes the probabilities of the semimeasure ![]() producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of
producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of ![]() stated in the abstract, which is different from the bound of
stated in the abstract, which is different from the bound of ![]() for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
Conclusion
In 2005, William Dembski made a radical change in what he called specified complexity, and developed the precursor of algorithmic specified complexity. He presented the “new and improved” specified complexity in terms of statistical hypothesis testing. That much of what he did made good sense. There are no formally established properties of algorithmic specified complexity that justify regarding it as a measure of meaningful information. The one theorem that Marks et al. have published is actually a special case of a 1995 result applied to hypothesis testing. In my own exploration of the properties of algorithmic specified complexity, I’ve seen nothing at all to suggest that it is reasonably regarded as a measure of meaning. Marks et al. have attached “meaning” rhetoric to some example applications of algorithmic specific complexity, but have said nothing about counterexamples, which are quite easy to find. In Evo-Info 5, I will explain how to use the methods of “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” to measure large quantities of “meaningful information” in nonsense images derived from the context.
The Series
Evo-Info review: Do not buy the book until…
Evo-Info 1: Engineering analysis construed as metaphysics
Evo-Info 2: Teaser for algorithmic specified complexity
Evo-Info sidebar: Conservation of performance in search
Evo-Info 3: Evolution is not search
Evo-Info 4: Non-conservation of algorithmic specified complexity
Evo-Info 4 addendum
[Some minor typographical errors in the original post have been corrected.]



Exactly!
Utter, and utterly classic, creationist pap. There are no “mathematical first principles” in science. There are no particles in mathematics.
The Blind Watchmaker: Why the Evidence of Evolution Reveals a Universe without Design, by Richard Dawkins.
Eric Holloway is ignoring the fact that Dembski lifted specified complexity — the property of being statistically improbable in a direction specified not with hindsight alone — from Dawkins’s book, without attribution. Yet Dembski is a great guy, and I’ve taken to badmouthing him for no good reason. (And Winston Ewert is now a great scientist, though he was such a dope as to copy more than half of the introduction to his master’s thesis from two papers by Dembski and Marks.)
In an earlier comment, I wrote:
How did Eric Holloway do on the test?
That “something important” he’s missing is the point, which is something that most readers of the plain-language portion of the OP can get: The algorithmic specified complexity of data, relative to the context, is not conserved under processing of the data. Simple processing — even corruption — of data can produce a huge increase in the algorithmic specified complexity of the data. The mathematical part of the OP shows that there is no limit to the possible increase.
So now Eric claims to have had a different, and furthermore bizarre, notion of conservation in mind:
I showed above that Eric misused the term Kullback-Liebler divergence, and his response indicated that he really didn’t care whether or not he used the term correctly. Some mathematician! What’s truly amazing is that Eric is convinced that people care to know what vague ideas he has in mind. A point I emphasized in the opening paragraph of the OP is that Dembski sketched a proof-idea that he had in mind, back in 2002, but never managed to produce the proof. You might think that Eric would get the message that one must do the math before talking about it. He evidently did not.
Now for the truly flagrant crackpottery… Having said no more about his private notion of conservation than what I’ve just quoted, and ignoring the details I have spelled out regarding non-conservation, Eric launches into talk about the “ASC conservation law” as though it were something he’d established.
Say what!? This is just gobbledygook. If you’re ID-friendly, and you were thinking, “Wow, I don’t know what this guy’s saying, but he’s got to be smart,” then you need to understand that you’ve been fooled. Eric Holloway is not in the same class as William Dembski. He’s not even in the same class as Winston Ewert. (Lest you think that I insult the intelligence of all the younger ID proponents, I should mention that I recognize George Montañez, who did his master’s work under the direction of Bob Marks, as a very bright guy.)
Emphasis added. Eric is aware, at some level, that he’s just treated us to word salad. There was nothing to keep him from doing a bit of “tying these things together” here. He has not produced a comprehensible proposition, let alone a proof. Yet he yammers with apparent conviction that there’s something very special about his yammering. I’m here to tell you, it’s just yammering. If this nonsense coming from Eric Holloway is the future of ID, then the outlook for the ID movement is very bleak indeed.
The OP is primarily a response to Marks, Dembski, and Ewert, who have remarked on the formal similarity of algorithmic specified complexity to algorithmic mutual information. The similarity of the two is something that I first considered five years ago. However, it was Eric Holloway’s zany servings of mathematicalistic word salad, hither and yon in cyberspace, that motivated me to get down to the hard work of figuring out what to post.
You don’t have to follow the mathematics in the OP to understand that I have turned an image into nonsense, and thereby increased the amount of “meaning” in it, as measured by Marks et al., from 13 megabits to 24 megabits. This is all the more embarrassing for the fact that what Dembski said about specified complexity as a test statistic, back in 2005, makes vastly more sense than what he and his colleagues are saying about it today. The ID movement is losing ground, not making headway, in the dimension of basic sanity of claims.
Word salad can be tasty with the right dressing.
Thanks Tom.
Tom English,
Considering you are an objective seeker of truth and you are showing that there is a gap between these definitions and biological functional information how do you recommend we proceed? How do we move from mass confusion to enlightenment?
Gee, my prompts aren’t prompting anyone to do anything. I had better take the direct approach:
Please ask questions about the OP.
Several years ago, Alan Fox asked a question that he supposed was dumb. The way he put the question led me to explain things differently than I had before. Joe Felsenstein saw in my response something important that I never would have seen myself. It’s the single most valuable insight into ID I’ve ever had. And I’m telling you that the having of that insight was collaborative. I’ll be writing, in Evo-Info 6, about conservation of active information (not specified complexity) as an obfuscated application of something very simple, Markov’s inequality. I’ll be acknowledging the contributions of both Alan and Joe.
Tom’s Koan of the Day: What is enlightenment if you die in the moment of attaining it?
When it comes to science, I’m purely a pragmatist. The truth of a scientific account is in its working in some way that does not depend on the private beliefs of observers. Of course, what it means for one account to work better than another is complicated.
I’ve noted before that Hazen et al. put “functional information” in scare quotes, and treated it as a measure of complexity, not as a measure of information. I don’t see any sense in regarding it generally as a measure of information.
You make it sound as though there’s a gap between definitions and the physical reality of “biological functional information.” I’ve explained before that “functional information” is an explanatory construct of ours. We identify a space of configurations, and we decide how to dichotomize the configurations. Nature itself does not tell us where to draw a line between “functional” and “non-functional” configurations. It’s only after we’ve decided how we’re looking at a physical system that the measurement (usually an estimate) of functional information is objective. The functional information isn’t really “out there.” It’s something that we’ve constructed, and the question is whether our construct helps us develop explanations that in some sense or another “work” better than previously developed explanations.
Algorithmic specified complexity is measured on the encoding of an individual object as a binary string (finite sequence of 0s and 1s). “Functional information” is measured on the entire ensemble of configurations of a physical system. It’s just log(1/p), where p is the proportion of configurations that we classify as functional. I wrote proportion instead of probability because there’s no stipulation in the definition of “functional information” that the configurations arise by a random process, let alone that they arise uniformly at random. In contrast, Marks et al. are saying that there is a random object-generating process. So there’s indeed a deep gulf between algorithmic specified complexity and “functional information.” I don’t know why you would expect the gulf to be bridged, apart from the fact that the word “information” is tossed around in connection with both. They’re actually very different concepts. And I emphasize that I just wrote concepts, not natural entities.
Very well put.
Thank you, Tom.
One of the issues is we are steeped in a information technology culture, and are used to hear words like “bits”, “sequence”, “algorithm”, “program”, “copying” and similar terms all the time, and we all have some sort of idea of what they mean in every day language.
The situation isn’t helped by the fact that the FI sensu Hazen et al. is measured in “bits”. This implies a quantity, something that there can be more or less of, and it’s bits of course and information can be stored in bits like on a hard drive, and well it’s used for entities in biology, such as protein or DNA sequences, and they *do stuff* that *functions in some way* to allow some organism to persist and survive, so it’s “functional information”. But.. what IS that anyway?
The problem is it’s not at all clear what that “information” is. We normally think of information as being about something. A book is about something. It’s about events. Recordings of experiences, people, places, their properties, their actions and so on. But what is functional information? What is it about? It’s not about anything. It’s not information in that sense. I’m not convinced it is even a useful concept. What can we do with it? Who’s research is improved by it? If I want to create a new enzyme, or a drug, or I want to find out what gene interacts with another gene in order to understand some disease state at the cellular or molecular level, how does this FI thing help me? Has it ever helped anyone do anything? I suspect the answer is no and I’ll happily take correction here. But from where I sit it looks like masturbation without the happy ending.
What is it for?
Tom English,
They both involve strings. One is represented by two voltage levels in computers and one is represented by 4 nucleotides in DNA. In the computer case if that string of voltage levels (representing1 and 0) is in the right order it can execute a computer program. In the case of the 4 nucleotides if they are in the right order they can build a protein or perform other regulatory functions. In both these cases order matters and maybe thats where the bridge is or where the land separating water is.
In my mind part of the ID argument comes down to the origin of the order observed. If Demski’s argument never addressed the order of the string or sequence then your complaint is valid. Mutual information appears to be comparing the order of two strings if I understand it at all.
When order matters then we observe the possibility of almost infinite potential arrangements. If meaningful (can execute a computer program or generate a protein) ordered arrangements are even scarcely rare we only have one known mechanism that can create them.
No, we don’t.
The analogy between bits in a computer program and nucleic acid bases makes me wince. Speaking as an IT-employed biochemistry graduate!
Two, it’s at least two. As far as I’m aware, people such as computer programmers write computer programs. People don’t design genomes, except when exploiting evolution (such as in plant or animal breeding). People weren’t around when the basic work was being done 3 – 4 billion years ago.
If ID proponents could demonstrate a capability in discerning a meaningful DNA sequence from a non-meaningful sequence, I’d be impressed. The mathematical approach so far has proved useless. I think there’s a fundamental problem, that in a non-deterministic universe, an object does not carry all its history with it. No amount of manipulation of parameters will elucidate it. So the claim that it is possible to tell “designed” from evolved is bound to fail.
But to really impress me, how about reading DNA language? Given a lengthy sequence, predict the properties of the relevant synthesized protein. Can’t do it, can you! (Unless you synthesize the protein and test it for function – rather like evolution is supposed to).
Cargo cult science remains a valid charge till ID proponents get their hands dirty.
In the subsequent paper by Hazen et al, it is used to characterize complexity. The authors then go on to show how Avida simulation demonstrates that evolution can increase complexity and functional information, contra ID claims.
So it seems FI is not useful for biology, but rather it is useful for biologists to argue against ID. Which I find amusingly ironic.
Durston’s work then goes on to compound the irony by using FI as part of an argument for ID.
You cannot know how scarcely rare, and you cannot know how many arrangements can be considered “ordered” in the sense that they’d produce a functioning protein.
The “mechanism” you’re thinking about depends, at every level, on too many of those functioning arrangements, and thus it cannot have produced them. I can think of another mechanism though, and it doesn’t depend on as many of those functioning arrangements, and it’s easy to think how it could start with even much much much much simpler arrangements: evolutionary processes.
Entropy,
The mechanism I am talking about created the above arrangement of ordered strings. Can you produce an evolutionary model that can do the same? If the mechanism is understood this should be a chip shot.
😀
I thought you might get a kick out of that bit of semi-seriousness. It takes a certain flexibility with regard to seeing both sides of an issue…!
To me personally this is a self-defeating statement… I’m not trying to be disrespectful…
Eric has already stated it more than once that his theory/arguments may not apply to biology…
What makes you think that your attempts of making sense out of a cloud picture does?
Anyway, I think you, and probably all the supporters of this speculative math, should look at some testable models that can either prove or disprove the never ending speculations about FI…
Have you ever explored Grover’s Algorithm? If you had, as a mathematician, you could easily see that Grover’s Algorithm is optimal. What this means, in simple terms describing quantum mechanics, it that IF the fundamental blocks of life, like DNA 4 base pairs, and 20 amino-acids used by life systems, have evolved, they had to have used Grover’s quantum searching algorithm for optimal, error free replication…
What I’m wondering about is who or what figured out the Grover’s Algorithm first?
When Grover published his algorithm, he had no idea it applied to DNA base pairs and amino-acids. Some other scientists have done some calculations and realized that 4 DNA base pairs and 20 amino acids (plus the codon) resolve the optimisation problem…
If anyone needs evidence for ID/God/Designer, he/she/them don’t need to read the Free Lunch Theorem… This is it…
Here are the links:
https://arxiv.org/abs/quant-ph/0002037
Nor am I.
I want to mention that there are different senses of “information.” In algorithmic information theory, we have a clear, operational understanding of the amount of information in a binary string — somewhat oversimplified, it’s the length of the shortest binary computer program that outputs the string. I’ve never encountered anyone who did not find this intuitively appealing. (If you can store 100 megabytes of data in a self-extracting zip archive of size 10 megabytes, and then run the self-extracting archive to recover exactly the 100 megabytes of data you began with, the meaning of “information” is fairly clear when I say that there cannot have been more than 10 megabytes of information in the data.) We have a good, though somewhat technical, rationale for regarding this measure of information as “universal.” But there’s no “about” in this sense of “information.” Then again, when we define the algorithmic mutual information of two binary strings, it is natural to talk about the amount of information that two strings provide about each other.
In short, I think there are sensible usages of the term information that are not accompanied by about.
This, I think, is the million-krone question about “functional information.” How do we use it to improve explanations of what we observe in nature?
AIUI, the motivation was to have a metric for the way the “slope” changes with “altitude” for a variety of different functions :
Szostak, 2003
Nothing more.
Treating it as if it was a quality that must have a source (like enthalpy) is painfully stupid.
Thalidomide and cakes both involve organic molecules, and both relate to birthdays.
Sorry, but I see no sign of any understanding at all. In classical information theory, mutual information is defined on two probability distributions. Evidently you mean algorithmic mutual information, which is defined on two binary strings. When binary strings x and z are said to be high in algorithmic mutual information, the meaning is basically that each can be used to improve the compression of the other. That is,
is loosely “the length of the shortest program that outputs x on an empty input” minus “the length of the shortest program that outputs x on input of the shortest program that outputs z.” I’ve honestly struggled to find something right in what you’ve written, and have come up with a blank.
I suspect that the last sentence is actually your starting point. You’re repeating something that’s been said many times over the past 15 or so years. I think you understand “the origin of information requires intelligence” at the rhetorical level, but wade far out of your depth when you try to talk about mathematical formalisms. I’d encourage you to take inventory of your strengths and weaknesses, and to try to avoid playing to the latter.
DNA_Jock,
I’d forgotten that passage of Szostak (2003) entirely. So he indicated what the utility of the measure might be. He didn’t declare, in the manner of the Wizards of ID, that he’d come up with the best thing since sliced bread.
How many years ago was it when the “genetic regulatory network” abstraction supplanted the weak “genetic program” analogy? At least 25, I’d say off the top of my head.
The funny thing is that even Dawkins went with an analogy to a recipe, not an analogy to a computer program, in The Blind Watchmaker (1986).
Tom English,
Do you have an example how you would compare the mutual information given this formula?
1. Compare the algorithmic mutual information to what?
2. The algorithmic mutual information is not computable, though approximable.
Just wanted to let you know that I am definitely keeping up with this discussion, but am completely at a loss to even ask the dumbest questions. I hope that either Eric returns soon with his treatment of Joe’s haploid wombats example (of which I can reproduce the mathematical treatment), or that your notebook is released so I can try to reproduce the calculation of ASC in the PNG images.
OK, one question. What is supposed to be the context for the calculations of the ASC in a biological example of evolution? My gut feeling tells me it is supposed to be the allele frequencies of the initial population, but without any biological example I am just guessing. Do you know? Does Joe?
I mentioned this before, I think. My beef with Demsbki’s CSI is that it is supposed to answer something about a system’s history from an analysis of its present state. I don’t think strict determinism applies in this universe so I don’t think that such an inference is justified or possible.
A related point is that I think Tom is making a similar point as Lizzie did a while ago* using an image as an example to demonstrate that a digitally coded image string cannot be reliably distinguished from a random string.
*Couldn’t locate that thread? Anyone recall the title?
Tom English,
Estimate the AMI of two binary strings.
Alan Fox,
perhaps?
Not sure I agree about the consequences of a non-deterministic universe.
More to the point, I took Tom to be showing that he can convert a large, fairly compressible string into a similarly sized, virtually incompressible string, thus adding 11 megabits of ASC.
(Pictures just happen to be very familiar examples of fairly compressible data.)
According to the Law of Conservation of ASC, this conversion requires an algorithm of [at least??] 11 megabits.
His algorithm is, heh, somewhat shorter, and therefore the LoCoASC is false.
Yup, that’s the one. I see it was missing the author’s name. Thanks for finding it.
Well, someone tried to convince me, in a fully deterministic universe, know the present precisely and you know all the past and all the future. I suggest, therefore, in a universe that is not wholly determined at the moment of conception, that the past is not fully ascertainable from a precise knowledge of the present instant moment. Radioactive decay? Who can predict the moment a particular unstable nucleus will decay?
I guess I was jumping to the conclusion following the calculation. That it can tell you nothing about the origins of the image from the bitstring or manipulations thereof.
Something that stands out to me in your proof is that f changes the domain of X, but then you use the old domain to measure the probability of an event. However, if f just relabels events, then f can only preserve or increase probabilities (i.e. by merging labels). This is the reasoning behind the data processing inequality.
Apologies to several of you for having vanished.
You want to talk big and fancy when you’re not even performing at the sophomore level in your grasp of definitions. There is no capital- in what I wrote about non-conservation of ASC in the opening post. Even if you are referring to the little-
in what I wrote about non-conservation of ASC in the opening post. Even if you are referring to the little-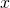 I wrote, it is nonsense to say that the function
I wrote, it is nonsense to say that the function 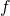 “changes the domain” of
“changes the domain” of 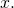 A function has a domain. It doesn’t change the domain of anything. The domain and codomain of
A function has a domain. It doesn’t change the domain of anything. The domain and codomain of 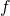 are both the set
are both the set 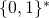 of binary strings, which includes the empty string
of binary strings, which includes the empty string 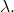 In the example of non-conservation that I constructed,
In the example of non-conservation that I constructed, 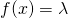 for all
for all 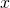 in the domain
in the domain 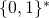 of
of 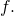 You would be right if you were to say that the range of
You would be right if you were to say that the range of 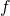 is the set
is the set 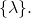 You also would be right if you were to say that
You also would be right if you were to say that 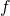 is a constant function.
is a constant function.
You would be evincing a modicum of insight into my counterexample if you were to observe that the shortest program realizing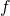 is the shortest program that does nothing but to halt on all inputs. For conventional definitions of universal prefix machine
is the shortest program that does nothing but to halt on all inputs. For conventional definitions of universal prefix machine 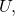
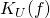 is the length of the shortest of all halting programs for
is the length of the shortest of all halting programs for 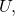 and the equality
and the equality
holds strictly for all binary strings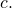 (Whether the equality holds only up to an additive constant, rather than strictly, for some universal prefix machines, I do not know.) The upshot is, loosely, that I have demonstrated non-conservation with the simplest of all possible data processing
(Whether the equality holds only up to an additive constant, rather than strictly, for some universal prefix machines, I do not know.) The upshot is, loosely, that I have demonstrated non-conservation with the simplest of all possible data processing 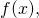 i.e., ignoring the input entirely, leaving the output empty, and halting. Furthermore, I have imposed only a light restriction on the probability distribution
i.e., ignoring the input entirely, leaving the output empty, and halting. Furthermore, I have imposed only a light restriction on the probability distribution 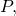 i.e.,
i.e., 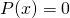 if and only if
if and only if 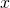 is the empty string. The consequence is that for all binary strings
is the empty string. The consequence is that for all binary strings 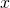 and
and 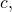
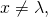
and
and hence
In plain language, what I have done is to exhibit a data processor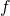 and a distribution
and a distribution 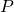 of probability over the possible data such that data processing
of probability over the possible data such that data processing 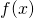 results in infinite gain of algorithmic specified complexity for all data
results in infinite gain of algorithmic specified complexity for all data 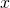 other than the empty string. The choice of context data
other than the empty string. The choice of context data  is irrelevant to this exhibition of non-conservation of ASC.
is irrelevant to this exhibition of non-conservation of ASC.
You seem not to recognize that this is a proof by counterexample, and that I might give other counterexamples, were you to raise an objection to the one that I’ve given. You have not bothered even to raise an objection. Instead you’ve blathered about something else:
However!? This is supposed to be an objection? I can only guess that you regard posting such vacuous gobbledygook as some sort of face-saving measure. You ought to be awfully embarrassed, when given a formal argument, to spew stuff like this in a public response. You wrote in your opening post “Breaking the law of information non growth“:
Although you have peppered your comments with mathematicalism, which probably impresses the rubes, you have posted nothing at all that is “technical and focussed.”
(By the way, I composed this comment in a Markdown cell of a Jupyter notebook, and then copied-and-pasted it into the comment box.)
Yes, I’ve been thinking about your proof for the past couple weeks and am looking for free time to write up what I consider to be a mistake in the proof. I don’t have a lot of time for back and forth, which is why I need to write a blog post that carefully defines everything.
I tried the quicker route in my last comment, but obviously my point was not communicated clearly.
Here is one more shot in a comment, and then hopefully this weekend I’ll be able to write it up:
The basic problem revolves around the fact that a random variable is a labeling of events from a probability distribution. Hence, when you apply a function to a random variable, as you are doing, all that is happening is you are relabeling the events. This means that function application can only change probabilities by merging two events by giving them the same label, which only increases the probability. Function application cannot split a label into multiple labels and decrease probabilities. Consequently, it is always the case that I(f(x)) <= I(x), which furthermore means that ASC(f(x),C,P) <= I(x).
Now, if function application could split labels, or change the experiment outcomes themselves that define the probability distribution (the domain), as you seem to be doing here, then I can see your argument working. But this would be a treatment of random variables that I am unfamiliar with. If this is what you have in mind, perhaps you can provide a reference so I can read up further on the matter.
PS if you can let me in on the secret of how to write Latex on this blog I’d be grateful.
TSZ has the WordPress plugin “WP QuickLaTeX” installed and enables site-wide.To include LaTeX in text just enclose it in single dollar signs. To add a separate line of equation, etc enclose it inside double dollar signs. so if I use sinle dollar signs around 2+2=4, I get and if I enclose in double dollar signs, I get
and if I enclose in double dollar signs, I get
Hope that helps. There’s a couple of snags, no preview and the text editor strips backslashes if you edit. See Tom’s comment upthread about using a text editor for easier working.
See this Eric ^^^
No, it was not a failure in communication. You were, and still are, talking nonsense.
Garbage. If you were a sophomore student of mine, I would write out something correct that somewhat resembles what you have written, and give you half credit. A Ph.D. engineer who confidently spouts stuff like this deserves negative credit, which is to say, derision.
How many times do I have to tell you that when I write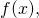 the function
the function 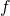 is defined on the set
is defined on the set
of binary strings, and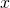 is a string in
is a string in 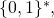 i.e., a finite sequence of 0s and 1s?
i.e., a finite sequence of 0s and 1s?
I am approaching my wit’s end, trying to deal with someone who insists on turning into a random variable an object that I’ve clearly and repeatedly identified as a binary string.
You leave me to guess that when you write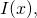 you follow Marks et al. in defining
you follow Marks et al. in defining
for all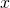 in
in 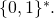 But then
But then 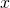 denotes a string, not a random variable. Indeed, the inequality
denotes a string, not a random variable. Indeed, the inequality
(evidently what you meant to write) does not make sense when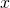 denotes a random variable, inasmuch as the expression on the left-hand side is not single valued. So the very most generous assumption I can make here is that you actually do not mean to say that
denotes a random variable, inasmuch as the expression on the left-hand side is not single valued. So the very most generous assumption I can make here is that you actually do not mean to say that 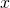 is a random variable. However, with my stipulations above that
is a random variable. However, with my stipulations above that 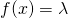 for all
for all 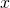 in
in 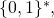 and that
and that 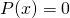 if and only if
if and only if 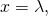 it follows from the definition of ASC that
it follows from the definition of ASC that 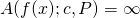 for all
for all 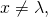 as I showed in the comment you’re responding to (and also in the OP). You do not get to drop in now, and simply dump on us a contrary assertion. You’ve got to show where my derivation is wrong.
as I showed in the comment you’re responding to (and also in the OP). You do not get to drop in now, and simply dump on us a contrary assertion. You’ve got to show where my derivation is wrong.
As for your contrary assertion, it is not the case that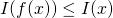 for all strings
for all strings 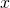 in
in 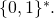 With the definitions of
With the definitions of 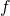 and
and 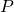 that I have given,
that I have given,
and
for all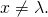 Now, my best guess of what mishap occurred in your head is that you attached the term “information” to both
Now, my best guess of what mishap occurred in your head is that you attached the term “information” to both 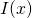 and the entropy
and the entropy
where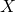 is a random variable with probability distribution
is a random variable with probability distribution 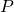 over
over 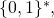 and hastily assumed that the elementary inequality
and hastily assumed that the elementary inequality
holds for “information”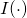 as for “information”
as for “information” 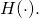
As for the notion that I’m nothing but a mean old man, well, I’ve just taken the trouble to diagnose your misunderstanding, and to spell out some details that may help you understand better.
Yes, I very much appreciate the time you are taking here. There is some sort of misunderstanding going on, most likely on my side, so I’ll work on a post writing everything. And, as frequently happens when I’m programming, I’ll probably discover my error in the midst of the write up 🙂 Again, thanks for you time and effort.
Also, you seem to disagree with my definition of a random variable:
Can you provide your own definition? The definition of a random variable is central to my (mis)understanding on this issue, so if we both are working from the same definition it would lead to clarity.
I took my definition from Wikipedia:
https://en.wikipedia.org/wiki/Random_variable
EricMH,
First, you respond to the substantive parts of my comment. Then I will flesh out the lead-in.
1. Do you understand that my demonstration of non-conservation of ASC involves no random variable?
2. Do you understand that, to reject my conclusion, you must show what is wrong with my derivation, and not merely argue for a contrary proposition?
3.a. Is the definition of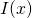 given by Marks et al. what you had in mind?
given by Marks et al. what you had in mind?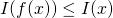 ?
?
3.b. Do you agree that it is not necessarily the case that
Indeed. Isn’t the whole point of algorithmic information theory that it does not involve any random variables, unlike Shannon information? That is what makes it so remarkable.
I’d never heard that before. Thanks Joe.
This is where we are talking past each other. My understanding of ASC is that it is testing whether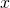 is sampled from a random variable defined by
is sampled from a random variable defined by 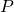 . That is what
. That is what 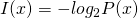 is measuring. As such, your proof does not work.
is measuring. As such, your proof does not work.
If we don’t agree on what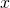 is, then we probably don’t have much to say to each other as we are talking about different things. So, I’ll have to drop the conversation here as I see this discussion devolving into an uninteresting semantic debate.
is, then we probably don’t have much to say to each other as we are talking about different things. So, I’ll have to drop the conversation here as I see this discussion devolving into an uninteresting semantic debate.
The correct reading of Dr. Ewert’s work is pretty clear in my mind, and nothing you’ve said here has persuaded me otherwise. Instead, it seems like you are purposefully misinterpreting his work in order to ‘prove’ it wrong, which I’ve seen happen over and over again in the past decade plus that I’ve been researching ID. One indication of your intent is that you consider the standard definition of a random variable problematic. The obfuscation tactic is pretty boring at this point, and reinforces my previous comment in this thread that the critics are uninterested in a fair minded reading of ID.
That said, I’ll probably still return here and to Peaceful Science occasionally, because in the midst of everyone’s attempt to obfuscate ID some interesting points are still made. Especially if the obfuscation is conducted in a highly formalized manner as you’ve done here, Dr. English. It’s like a murder mystery where I try and figure out where the guilty assumption or fallacious step lies. Hence, I still commend you for your obfuscating efforts.
What is not commendable is how you try to make trouble for ID researchers like Dr. Ewert. That casts you as a bully, and I don’t like bullies.
It is possible to introduce randomness into usages of K complexity. For example, one can relate K complexity and Shannon entropy by introducing a probability distribution in forming messages whose complexity is to be analysed.
This done in Cover and Thomas chapter 14.4 which starts
They show this roughly (eq 14.28)
– Suppose we have an alphabet.
– Let X be a random variable with that alphabet as its sample space
– Form messages of fixed length n by drawing letters independently from X
– Then as the messages get longer and longer (as n approaches infinity) …
the average K complexity of the message divided by its length n
approaches
the Shannon entropy of X, namely H(X)
As best I can tell from admittedly superficial reading Eric’s last message and Tom’s preceding ones, they disagree on whether randomness introduction is a necessary part of the definition of ASC.
Sorry to be so slow in my response. You prompted me to look over the past applications of ASC by Marks et al. After spending several hours on that, I launched into an overlong and meandering and probably unhelpful comment. I ended up discarding what I’d written.
My gut feeling is that if Marks et al. were to consider allele frequencies in the initial population, then they would calculate the active information of the process itself, not the specified complexity of the outcome, and would argue that the process must have been designed to produce the outcome that it (probably) does.
Since 2008, Marks et al. have reattached all of Dembski’s old “information” rhetoric, including “conservation of information,” to active information. Various passages in their book read much like Dembski’s No Free Lunch (2002), but with active information substituted for specified complexity. I had expected them to let specified complexity rot in an unmarked grave, as they have the explanatory filter. When they resurrected specified complexity, I was astonished, because what they were doing amounted to “heads, I win; tails, you lose”:
1. When the outcome of a process is more probable than they think it “naturally” ought to be, then they can attribute the elevated probability of the outcome to design of the process in which it occurs. This is what active information is “about.”
2. When the outcome of a process is very improbable, and yet easily describable in some context, then they can claim that the object is designed. This is what specified complexity originally was “about.” Dembski had said that specified complexity was a “reliable marker of intelligent design.”
In short, if the outcome is “too probable,” say that the process is designed, and if the outcome is “too improbable,” say that outcome is designed. Again, in response to your comment, I would expect Marks et al. to be taking the former tack when they get into the details of the process, e.g., the initial frequencies of alleles in the population.
When Ewert first talked about algorithmic specified complexity, at Jonathan Bartlett’s 2012 Engineering and Metaphysics conference, he said nothing about “meaningful information.” And I’ll surmise that there’s no mention of meaning in Ewert’s dissertation. As I recall, the first pitch of ASC as a measure of meaning is in the 2015 article “Algorithmic Specified Complexity in the Game of Life” (which is rife with errors). Tellingly, the “meaning” talk is concentrated in the introduction of the paper, which seems to have been written by Marks. In the body of the paper, which seems to have been written by Ewert, there is nothing about meaning. Instead, there is the ordinary concern with distinguishing functional configurations designed by humans from functional configurations arising from a random primordial “soup.” The key word here is functional, not meaningful.
I suspect that a biological application of ASC would look somewhat like the application to the Game of Life, and that the emphasis would be on use of the context, whatever it might be, to describe biologically functional configurations of matter. There’s far too much I might say on this issue, so I need to end things here, however unsatisfyingly, and encourage you to read “Algorithmic Specified Complexity in the Game of Life.”