Evo-Info 4 addendum

Posted on by
Introduction to Evolutionary Informatics, by Robert J. Marks II, the “Charles Darwin of Intelligent Design”; William A. Dembski, the “Isaac Newton of Information Theory”; and Winston Ewert, the “Charles Ingram of Active Information.” World Scientific, 332 pages.
Classification: Engineering mathematics. Engineering analysis. (TA347)
Subjects: Evolutionary computation. Information technology–Mathematics.

In “Evo-Info 4: Non-Conservation of Algorithmic Specified Complexity,” I neglected to explain that algorithmic mutual information is essentially a special case of algorithmic specified complexity. This leads immediately to two important points:

  1. Marks et al. claim that algorithmic specified complexity is a measure of meaning. If this is so, then algorithmic mutual information is also a measure of meaning. Yet no one working in the field of information theory has ever regarded it as such. Thus Marks et al. bear the burden of explaining how they have gotten the interpretation of algorithmic mutual information right, and how everyone else has gotten it wrong.
  2. It should not come as a shock that the “law of information conservation (nongrowth)” for algorithmic mutual information, a special case of algorithmic specified complexity, does not hold for algorithmic specified complexity in general.

My formal demonstration of unbounded growth of algorithmic specified complexity (ASC) in data processing also serves to counter the notion that ASC is a measure of meaning. I did not explain this in Evo-Info 4, and will do so here, suppressing as much mathematical detail as I can. You need to know that a binary string is a finite sequence of 0s and 1s, and that the empty (length-zero) string is denoted \lambda. The particular data processing that I considered was erasure: on input of any binary string x, the output \mathtt{erased}(x) is the empty string. I chose erasure because it rather obviously does not make data more meaningful. However, part of the definition of ASC is an assignment of probabilities to all binary strings. The ASC of a binary string is infinite if and only if its probability is zero. If the empty string is assigned probability zero, and all other binary strings are assigned probabilities greater than zero, then the erasure of a nonempty binary string results in an infinite increase in ASC. In simplified notation, the growth in ASC is

    \[A(\mathtt{erased}(x)) - A(x) = \underbrace{A(\lambda)}_\text{infinite} - \underbrace{A(x)}_\text{finite} = \infty\]

for all nonempty binary strings x. Thus Marks et al. are telling us that erasure of data can produce an infinite increase in meaning.

In Evo-Info 4, I observed that Marks et al. had as “their one and only theorem for algorithmic specified complexity, ‘The probability of obtaining an object exhibiting \alpha bits of ASC is less then [sic] or equal to 2^{-\alpha},’” and showed that it was a special case of a more-general result published in 1995. George Montañez has since dubbed this inequality “conservation of information.” I implore you to understand that it has nothing to do with the “law of information conservation (nongrowth)” that I have addressed.

Now I turn to a technical point. In Evo-Info 4, I derived some theorems, but did not lay them out in “Theorem … Proof …” format. I was trying to make the presentation of formal results somewhat less forbidding. That evidently was a mistake on my part. Some readers have not understood that I gave a rigorous proof that ASC is not conserved in the sense that algorithmic mutual information is conserved. What I had to show was the negation of the following proposition:

(False)   \[A(f(x); c, P) - A(x; c, P) \leq K(f) + O(1) \]

for all binary strings x and c, for all probability distributions P over the binary strings, and for all computable [ETA 12/12/2019: total] functions f on the binary strings. The variables in the proposition are universally quantified, so it takes only a counterexample to prove the negated proposition. I derived a result stronger than required:

Theorem 1. There exist computable function f and probability distribution P over the binary strings such that

    \[A(f(x); c, P) - A(x; c, P) = \infty\]

for all binary strings c and for all nonempty binary strings x.

Proof. The proof idea is given above. See Evo-Info 4 for a rigorous argument.

In the appendix, I formalize and justify the claim that algorithmic mutual information is essentially a special case of algorithmic specified complexity. In this special case, the gain in algorithmic specified complexity resulting from a computable transformation f(x) of the data x is at most K(f) + O(1), i.e., the length of the shortest program implementing the transformation, plus an additive constant.

Appendix

Some of the following is copied from Evo-Info 4. The definitions of algorithmic specified complexity (ASC) and algorithmic mutual information (AMI) are:

    \begin{align*} A(x; c, P) &:= -\!\log P(x) - K(x|c) &\text{(ASC)} \\ I(x: c) &:= K(x) - K(x|c^*), &\text{(AMI)} \\ \end{align*}

where P is a distribution of probability over the set \mathcal{X} := \{0, 1\}^* of binary strings, x and c are binary strings, and binary string c^* is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity K(\cdot) and the conditional algorithmic complexity K(\cdot|\cdot) are defined, outputting c. The base of logarithms is 2. The “law of conservation (nongrowth)” of algorithmic mutual information is:

(1)   \begin{equation*} I(f(x) : c) \leq I(x:c) + K(f) + O(1) \end{equation*}

for all binary strings x and c, and for all computable [ETA 12/12/2019: total] functions f on the binary strings. As shown in Evo-Info 4,

    \[I(x: c) = -\!\log M(x) - K(x|c^*),\]

where the universal semimeasure M on \mathcal{X} is defined M(x) := 2^{-K(x)} for all binary strings x. Here we make use of the normalized universal semimeasure

    \[M^*\!(x) := \frac{M(x)}{M(\mathcal{X})},\]

where M(\mathcal{X}) = \sum_x M(x). Now the algorithmic mutual information of binary strings x and c differs by an additive constant, \log M(\mathcal{X}), from the algorithmic specified complexity of x in the context of c^* with probability distribution M^*.

Theorem 2. Let x and c be binary strings. It holds that

    \[I(x : c) = A(x; c^*\!, M^*) - \log M(\mathcal{X}).\]

Proof. By the foregoing definitions,

    \begin{align*} I(x : c) &= K(x) - K(x|c^*) \\ &= -\!\log M(x) - K(x|c^*) \\ &= -\!\log(M(\mathcal{X}) M^*\!(x)) - K(x|c^*) \\ &= -\!\log M^*\!(x) - K(x|c^*) - \log M(\mathcal{X}) \\ &= A(x; c^*, M^*) - \log M(\mathcal{X}). \end{align*}

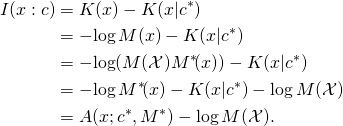
Theorem 3. Let x and c be binary strings, and let f be a computable [and total] function on \mathcal{X}. Then

    \[A(f(x); c^*\!, M^*) - A(x; c^*\!, M^*) \leq K(f) + O(1).\]

Proof. By Theorem 2,

    \begin{align*} &A(f(x); c^*\!, M^*) - A(x; c^*\!, M^*) \\ &\quad = [I(f(x) : c) - \log M^*\!(\mathcal{X})] - [I(x : c) - \log M^*\!(\mathcal{X})] \\ &\quad = I(f(x) : c) - I(x : c) \\ &\quad \leq K(f) + O(1). \\ \end{align*}

The inequality in the last step follows from (1).

153 thoughts on “Evo-Info 4 addendum”

  1. Thanks Tom.
    I’m uncomfortable with arithmetic involving infinity as in your equation for A(erased(x)) – A(x). Such transfinite arithmetic depends on some ideas in math which should not be needed in this context.

    Can your argument be made by instead showing how A(.) can be made arbitrarily large? If do do that, do you then have to deal with ID claims that the argument does not work because of limits on the :probability resources of the universe” (often involving 10**-120 or some such number).

  2. Hasn’t this objection already been answered? Nemati’s Bio-Complexity paper on conservation of ASC (section 4) seems to have already shown the issue here being incorrect function application (i.e., if you do a function mapping, you also have to remap probability spaces).

    Expected Algorithmic Specified Complexity

  3. BruceS: Can your argument be made by instead showing how A(.) can be made arbitrarily large?

    Yes, but I don’t particularly like doing it. 😉 If Marks et al. are going to rely on examples, rather than propose formal properties for a measure of meaningful information, and prove that ASC has them, then they should look for examples that refute their notions. I have a number of ugly examples that are permitted by their definition. If Marks et al. don’t like my examples, then they had better change the definition of ASC.

    As for your question… Pick the minimum increase \alpha > 0 in ASC you want to see when a nonempty string is deleted. We can define a probability distribution P over the binary strings such that

        \[0 < P(\lambda) \leq 2^{-\alpha} P(x)\]

    for all nonempty strings x. Then the increase in complexity on erasure of a nonempty string x is

        \begin{align*} -\!\log P(\mathtt{erased}(x)) - ( -\!\log P(x)) &= \log P(x) - \log P(\lambda) \\ &\geq \log(2^\alpha P(\lambda)) - \log P(\lambda) \\ &= \log 2^\alpha \\ &= \alpha. \end{align*}

    Unless you define Kolmogorov complexity in terms of some pathological universal computer I’m unable to imagine at the moment,

        \[K(\mathtt{erased}(x)|c) = K(\lambda|c) < K(x|c)\]

    for all nonempty strings x. (The shortest program that outputs the empty string is a program that simply halts. So \lambda should have the least Kolmogorov complexity of any string.) [ETA: Oops, I meant to provide you with this inequality also:

        \[K(\mathtt{erased}(x)|c) - K(x|c) = K(\lambda|c) - K(x|c) < 0\]

    for all nonempty strings x.] I leave it to you to put the pieces together, and obtain

        \[A(\mathtt{erased}(x); c, P) - A(x; c, P) > \alpha\]

    for all nonempty strings x.

  4. johnnyb: Hasn’t this objection already been answered? Nemati’s Bio-Complexity paper on conservation of ASC (section 4) seems to have already shown the issue here being incorrect function application (i.e., if you do a function mapping, you also have to remap probability spaces).

    Expected Algorithmic Specified Complexity

    Nemati and Holloway are sorely confused. I’m working on a response to their article. (I have to wonder also what was going on with the reviewers and editors who approved it.) As I said in the OP:

    Tom English: In Evo-Info 4, I observed that Marks et al. had as “their one and only theorem for algorithmic specified complexity, ‘The probability of obtaining an object exhibiting \alpha bits of ASC is less then [sic] or equal to 2^{-\alpha},’” and showed that it was a special case of a more-general result published in 1995. George Montañez has since dubbed this inequality “conservation of information.” I implore you to understand that it has nothing to do with the “law of information conservation (nongrowth)” that I have addressed.

    Do you not understand that Nemati and Holloway are addressing

    (1)   \[\Pr[A(X; c, P) \geq \alpha] \leq 2^{-\alpha}, \]

    where random variable X \sim P? See, for instance, their Eq. 54. It is utterly bizarre that they have lifted part of my argument out of context, and treated it as though it were a challenge to the inequality above: I indicated in Evo-Info 4 that inequality (1) was correct. In fact, I had proved a generalization of the result on my blog, back in 2015. Furthermore, George Montañez cited my post in his BIO-Complexity article of December 2018.

  5. Tom English,

    Marks et al. claim that algorithmic specified complexity is a measure of meaning. If this is so, then algorithmic mutual information is also a measure of meaning. Yet no one working in the field of information theory has ever regarded it as such. Thus Marks et al. bear the burden of explaining how they have gotten the interpretation of algorithmic mutual information right, and how everyone else has gotten it wrong.

    This needs to be addressed with more than an ad populum argument. I see you addressed that with a new op promised to Johnnyb. The other issue is to include CSI and its relationship to mutual information. Are they one in the same? If not what are the specific differences. As Joe F has mentioned before CSI is very similar to functional information defined by Szostak and Hazen.

  6. Tom English: Do you not understand that Nemati and Holloway are addressing

    (1) 

    where random variable ?

    We are addressing what it means to measure ASC(f(x),C,P). Either you have a new distribution as in your example, and thus infinite ASC shows the chance hypothesis is incorrect, and ASC works as expected. Or, you are transforming your random variable as we explain at length in the paper, in which case we prove an upper bound, which is not infinite. So either way your claim is incorrect.

  7. Eric,

    Either you have a new distribution as in your example, and thus infinite ASC shows the chance hypothesis is incorrect, and ASC works as expected.

    That doesn’t make sense to me. ASC is supposed to be a measure of meaningfulness, yet you’re saying that ASC “works as expected” when it attributes infinite meaningfulness to the empty string.

  8. keiths: ASC is supposed to be a measure of meaningfulness, yet you’re saying that ASC “works as expected” when it attributes infinite meaningfulness to the empty string.

    Well, a non response to a question can be a response as well, and thus mean something. ASC measures whether an event has a statistically significant relationship to an external context or not, and a null event can be such an event.

    My point is the mathematical properties of ASC are not violated by Tom’s example, and it actually demonstrates how ASC is meant to work. The new empty string is not part of the domain of the chance hypothesis, so its occurrence is impossible given the chance hypothesis. Thus, its occurrence demonstrates the chance hypothesis is false and some sort of outside agency intervened. This turns out to be the case in Tom’s example, b/c he intervenes in the chance hypothesis to apply his function.

    Now, I agree with Tom that ASC is not strictly conserved under stochastic processing. To use my awkward notation from the expected ASC paper, I only was able to derive an upper bound based on the initial complexity:

    E_F[fASC(x, p, C, F)] <= I(x).

    There is not the same beautiful sharp bound (as far as I can prove) that we have with algorithmic mutual information,

    E_F[I(F(x):y)] <= I(x:y)

    which may be what Tom is getting at.

    That being said, there is still a limit, and ASC cannot be increased arbitrarily high through stochastic processing.

  9. Eric,

    Well, a non response to a question can be a response as well, and thus mean something.

    But can the empty string carry an infinite amount of meaning? That seems far-fetched to me.

    Besides, ASC is supposed to be about intrinsic meaning, no? Otherwise the inclusion of the KC term would make no sense.

  10. Eric,

    Now, I agree with Tom that ASC is not strictly conserved under stochastic processing.

    If so, then how can it be used as a reliable indicator of design?

  13. keiths: If so, then how can it be used as a reliable indicator of design?

    The corner case I mention has to be specifically chosen out of the range of possibilities.

    If we range over all possibilities, as we must if we are using ASC properly, then the original conservation result Nemati and I prove in our paper still holds. Expected ASC is always negative, even when processed with a function, whether deterministic, random, or combination thereof. This means that regardless of how you process the events, such as with an evolutionary algorithm or otherwise, then when you take the average it will eventually converge to a negative value over enough samples.

    Alan Fox: Wondering why Tom’s OP hasn’t drawn more responses from ID proponents.

    I explained why his criticism is mistaken in my comment. The Bio-C paper Nemati and I wrote goes into more mathematical detail.

  14. Joe Felsenstein: The meaning of “meaning” seems to be unexplained.

    We have a discussion of the meaning of ‘meaning’ in our Bio-C paper. See section 2.

    Essentially, an event is meaningful when it points to something beyond itself, like a signpost.

  15. keiths: But can the empty string carry an infinite amount of meaning? That seems far-fetched to me.

    That is an interesting case. I’ve wondered too what infinite ASC implies. My best take is as follows.

    With finite ASC values, we have identified an event that is improbable but is still within the realm of possibility for the chance hypothesis. So, there is always a chance it is not meaningful and we just happened upon the event by accident.

    However, if we find an event with infinite ASC, then this means the event is entirely outside the realm of possibility when it comes to the chance hypothesis. Cast in terms of the physical world, we have seen some event that is completely inexplicable when it comes to the operating characteristics of the physical world, and thus necessitates an otherworldly explanation, instead of merely making such an explanation more probable.

    As for erasure, one such inexplicable event could be the entire universe suddenly popping out of existence. If such a possibility is excluded by the laws of physics, then the popping out of existence would require the intervention of something outside the laws of physics. I think at least in the Bible such an event is described, where the very elements of physical reality are destroyed.

  16. I chose erasure because it rather obviously does not make data more meaningful.

    EricMH: However, if we find an event with infinite ASC, then this means the event is entirely outside the realm of possibility when it comes to the chance hypothesis.

    Now I am confused. Are we talking about the event (erasure) or the information contained within the string?

  17. Now I am confused. Are we talking about the event (erasure) or the information contained within the string?

    One biological example might be comparing an organisms DNA with another organism without DNA.

  18. colewd: One biological example might be comparing an organisms DNA with another organism without DNA.

    You know of lots of living creatures which have no DNA, eh Bill?

  20. EricMH: We are addressing what it means to measure ASC(f(x),C,P). Either you have a new distribution as in your example, and thus infinite ASC shows the chance hypothesis is incorrect, and ASC works as expected.

    There is no “new distribution.” Show it to me, or admit that you were wrong. “Show it to me” does not mean “double down on nebulosity.” Write out the mathematical expression.

    EricMH: Or, you are transforming your random variable as we explain at length in the paper, in which case we prove an upper bound, which is not infinite.

    The claim that you prove an upper bound is not just incorrect. It’s a lie. The upper bound is on fASC, which you defined for no other reason than to produce an upper bound. Specifically, from Equation (43):

    fASC(x, C, p, f) < I(x).

    The upper bound on fASC says absolutely nothing about ASC. All that you have done in the article is what you are doing here, namely, to conflate fASC with ASC rhetorically while failing to engage, let alone refute, my proof that data processing can result in infinite increase in ASC.

    You really need to get a handle on yourself, Eric. I see in your paper that you are genuinely confused about quite a lot. But you are not so confused that, when you go out of your way to define something very different from ASC, fASC, you think that fASC actually is ASC. Thus when you refer to fASC as ASC here, you are lying. Please, for your own sake, stop.

  21. EricMH: ASC measures whether an event has a statistically significant relationship to an external context or not…

    Garbage. There is nothing in the definition of ASC that requires the context C to be used in compressing the binary string x, which is to say that K(x|C) is not necessarily smaller than K(x).

    By the way, you define event nowhere in your article, and you evince ignorance of probability theory with your use of the term.

  22. EricMH: My point is the mathematical properties of ASC are not violated by Tom’s example, and it actually demonstrates how ASC is meant to work. The new empty string is not part of the domain of the chance hypothesis, so its occurrence is impossible given the chance hypothesis.

    Wow, Eric. For a PhD in ECE, that is just plain dopey. The domain of a probability distribution over the set of all binary strings does include the empty string, irrespective of whether the empty string is associated with a positive probability. If the probability of the empty string is zero, then the empty string is not in the support of the distribution.

    Thus, its occurrence demonstrates the chance hypothesis is false and some sort of outside agency intervened. This turns out to be the case in Tom’s example, b/c he intervenes in the chance hypothesis to apply his function.

    You’re talking out of both sides of your mouth. You say that ASC is a measure of meaningful information. But in cases where it obviously is not a measure of meaningful information, you say that everything is hunky-dory ‘cuz ASC is for statistical hypothesis testing. It was I, not you, who endorsed the latter in Evo-Info 4 (November 2018, several weeks before George Montañez adopted a similar perspective in a Bio-Complexity article, and made no mention at all of meaningful information).

    The “meaningful information” claims are utter bullshit. Too bad you dumped a load with your dissertation.

    How, precisely, do you get “some sort of outside agency intervened” as the alternative hypothesis? The obvious alternative hypothesis is that an algorithmically simple process transformed the context into the observed outcome x. Part of why I chose erasure f(x) = \lambda is that, for conventional universal prefix machines, the very shortest of halting programs is the program that does nothing but to halt (with the empty string as its output). I contend that the probability that a randomly selected program computes f is not small. Are you really going to argue that erasure of data is a sign of intelligence? All it indicates is that m_{/C} is a better model than p.

  23. EricMH: Now, I agree with Tom that ASC is not strictly conserved under stochastic processing. To use my awkward notation from the expected ASC paper, I only was able to derive an upper bound based on the initial complexity:

    E_F[fASC(x, p, C, F)] <= I(x).

    That is not “awkward notation.” There is no corresponding bound for ASC. As I said before, you intentionally defined fASC to be very different from ASC. So it is not an accident that you are misleading people by referring to fASC as ASC. It is a lie. Again, please abandon that tack.

  24. EricMH: If we range over all possibilities, as we must if we are using ASC properly, then the original conservation result Nemati and I prove in our paper still holds. Expected ASC is always negative, even when processed with a function, whether deterministic, random, or combination thereof.

    False. You merely assert the inequalities for ASC in (45) and (46), as shown in the attached screen grab. By the way, (46) makes sense only with an uppercase L. What is it about you, that you think you can go around tossing off stuff like this, and get it right? The inequalities you give for ASC are both generally false when X is distributed according to p. I already have proofs. But you, as the person who published this stuff without proof, really are obligated to go first. Either put up some formal proofs, or confess that you published none because you have none. (Prepare LaTeX in your preferred environment. Then copy-and-paste. In a comment, you’ll have to change the < symbol to HTML &lt; To number equations, you have to use \tag.)

    You told us for a year about this big paper of yours that was coming, and it’s truly amazing to find that you’ve used it to lay on with more naked assertions.

  25. Joe Felsenstein,

    He doesn’t know any, but boy, if there were one, it would be dynamite!

    If there is not a condition with an animal with no DNA then why is Tom making an issue with the infinity in Eric’s equation caused by an empty set?

    Is Tom doing anything more than odhominem attacks based on a quibble?

  26. colewd: If there is not a condition with an animal with no DNA then why is Tom making an issue with the infinity in Eric’s equation caused by an empty set?

    It’s not just about DNA, but about any data that can be expressed as a bitstring. For example, it means that using ASC as a metric of meaning, erasing all the text in the Bible could, in principle, make it infinitely more meaningful*. Surely you agree that can’t be right?

    ETA: *depending on the probability distribution one is using

  27. Corneel,

    It’s not just about DNA, but about any data that can be expressed as a bitstring.

    You agree that Tom’s objection is only theoretical in nature with no application to biology? If Eric were to say that his “proof” applied to all non zero bit streams we can call it a day? Given his proof is directed toward biology would that make sense?

  28. colewd: You agree that Tom’s objection is only theoretical in nature with no application to biology? If Eric were to say that his “proof” applied to all non zero bit streams we can call it a day? Given his proof is directed toward biology would that make sense?

    As far as I am concerned, everything about ASC is “theoretical in nature with no application to biology”, including Eric’s ponderings in the bio-complexity paper.

    But, as I understand it, Tom’s objection to Eric’s use of ASC goes a bit deeper than whether it can be applied to biological sequences. He takes issue with the claim that ASC is a measure of “meaningful information”. If an empty string can have infinite meaning, the metric is clearly not doing its job.

  29. Corneel,

    But, as I understand it, Tom’s objection to Eric’s use of ASC goes a bit deeper than whether it can be applied to biological sequences. He takes issue with the claim that ASC is a measure of “meaningful information”. If an empty string can have infinite meaning, the metric is clearly not doing its job.

    I know this is the objection but is it more than an arbitrary way to disqualify Eric’s argument? An empty string does not support the math….so what? We don’t have empty strings in biology.

    The real issue on the table is whether we can produce de novo information algorithmically. Eric’s argument makes an interesting case along with no living example of an algorithm creating de novo information.

  30. colewd: along with no living example of an algorithm creating de novo information.

    Why do you keep repeating this lie when you’ve been shown countless empirical examples of new information creation in living species?

  31. Corneel,

    In addition is this statement true?
    I(f(x)) = −log2 p(f(x)) = − log2 0=∞ (. 28)

    Is there a valid argument that -log2 0 is undefined?

  32. Adapa,

    Why do you keep repeating this lie when you’ve been shown countless empirical examples of new information creation in living species?

    We know there is new information what we don’t know is the mechanism. We know minds can create this information we don’t know an algorithmic process can. We have good reason to believe an algorithmic process cannot.

  33. Corneel,

    Howard Ludwig, Ph.D. Physics, Northwestern University (1982)
    Answered Nov 30, 2017 · Author has 1.3k answers and 2.6m answer views
    Originally Answered: What is the exact value of log 0?
    The exact value of log 0 is exactly “undefined”. You did not specify a base for the logarithm, but this answer is independent of the base.

    Another way of phrasing this is that 0 cannot be an element of the domain of log, so you are forbidden to apply log to 0.

    It is not a matter that nobody has yet been smart enough to figure out the correct, exact value but people are working on it trying to figure it out. No, quite the opposite—mathematicians have proven that log 0 cannot be assigned any meaningful, useful value because such a value does not exist to be found.

    This guy seems to believe log 0 is undefined and independent of the base.

  35. Tom is providing what is known as a counterexample. A standard thing to look for in mathematics. There are other possible numerical examples that could also be used as counterexamples. If colewd wants to claim that the conservation of ASC may not be true in general but is true for all biologically realistic cases. he should consider that (1) that’s not what EricMH asserted, and (2) that assertion needs a proof. Neither colewd nor EricMH has provided a proof of that.

  36. Joe Felsenstein: Neither colewd nor EricMH has provided a proof of that.

    Neither you nor Dr. English seem to have read the Bio-C paper, where said proof is provided. If you think there is a problem with my Bio-C paper, or with Dembski’s conservation of information, then you need to submit a criticism to Bio-C. Otherwise, there is not enough time for all this back and forth. I have provided a clear enough explanation in numerous comments for those who really want to understand, both in regards to Dr. English’s criticism and Dr. Felsenstein’s criticism. For the rest who just want something to complain about, well there’s nothing much else I can say. Complain away.

  37. Well I’m late to the party, as usual. Some of you know me by a different name, but I’ve used this handle here for years and I’m sticking with it. If necessary, inquire at Peaceful Science.

    EH: Well, a non response to a question can be a response as well, and thus mean something.

    There can be a default state, or a Bayesian Prior assumption, but by definition an empty string cannot carry information, or even indicate an attempt to transmit a message.

    colewd: This [interpretation of algorithmic mutual information] needs to be addressed with more than an ad populum argument.

    The interpretation of Kolmogorov Information has been around since 1963, and it is a measure of compressibility – having nothing at all to do with meaning. This is hardly an ad populum argument.

    keiths: Besides, ASC is supposed to be about intrinsic meaning, no? Otherwise the inclusion of the KC term would make no sense.

    ASC is measuring the (non-)compressibility of a string, yes? (Someone correct me if I have this wrong). There might be many strings of equal compressibility but different meanings, or no meaning at all.

    EricMH: My point is the mathematical properties of ASC are not violated by Tom’s example, and it actually demonstrates how ASC is meant to work. The new empty string is not part of the domain of the chance hypothesis, so its occurrence is impossible given the chance hypothesis. Thus, its occurrence demonstrates the chance hypothesis is false and some sort of outside agency intervened.

    My emphasis added – How is it possibly to conclude Outside Agency without some very strong Bayesian Prior about the existence of this Agency? Especially when the strongest proof is no information at all??
    At best the possibility of an empty string indicates your model has failed to account for all possible outside (ie: it’s wrong).

  38. EricMH: I have provided a clear enough explanation in numerous comments for those who really want to understand, both in regards to Dr. English’s criticism and Dr. Felsenstein’s criticism.

    No, you have not.
    I’ve seen a lot of hand-waving, but no attempt to address the fact that {conservation (non-growth) of Algorithmic MUTUAL Information} does not imply anything about {conservation (non-growth) of algorithmic specified complexity} .
    That’s something of a show-stopper. We’ve seen counter-examples, both in the action of functions on binary strings, and in realistic simulations of biology.

  39. Everyone:

    colewd: If there is not a condition with an animal with no DNA then why is Tom making an issue with the infinity in Eric’s equation caused by an empty set?

    I doubt that you will ever understand, but I will note anyway that the equation is not Eric’s (the definition of ASC comes from Ewert, Dembski, and Marks), and the infinity is not “caused by an empty set.” The infinity comes from a probability of zero in the denominator of a fraction. Part of the definition of the ASC is

    A(x; c, p) := log(1 / p(x)) – …

    for all binary strings x, where p is a distribution of probability over the set of binary strings. The probability distribution is not given to us by nature. In a probabilistic model of a process with a binary string as an outcome, the modeler assigns probabilities to all of the binary strings. The smaller the probability p(x) that the modeler assigns to binary string x, the greater the improbability 1/p(x) and the log-improbability log(1/p(x)). As the probability approaches zero, the improbability and log-improbability both approach infinity.

    I did not have to assign probability zero to the empty string λ in order to refute Eric Holloway’s unwarranted and oft-repeated claim that ASC is conserved in the sense that algorithmic mutual information is conserved. An advantage in doing so is that the part of the definition that I replaced with ellipsis (…) above is finite in all cases, and thus “drops out” when the log-improbability log(1/p(x)) is infinite. I can make the log-improbability as large as you like, without making it infinite, but at the cost of having to say more about the part of the definition of ASC that I omitted above, i.e., the conditional algorithmic complexity of x, K(x|c).

    =======

    To date, no ID proponent has published a biological application of ASC. (Eric Holloway has never limited his remarks to biology. In fact, he usually speculates on information in the cosmos, as in a comment above.) The credit for locating a biological application of algorithmic mutual information, which is essentially a special case of ASC (as shown in the OP), goes to me. In Evo-Info 4, I discussed an article from 25 years ago, in which Aleksandar Milosavljevic used an approximation of algorithmic mutual information in testing a biological hypothesis. Two Bio-Complexity articles of the past year take my reference to Milosavljevic from Evo-Info 4, but neither of them cites my post.

    In Evo-Info 4, I approximated the ASC of digital images, using precisely the assignment of probabilities to images that Marks et al. do in “Measuring Meaningful Information in Images: Algorithmic Specified Complexity.” I showed that irreversible corruption of an image by a very simple computer program results in a huge increase in ASC. Do please click on the link I just provided, and see for yourself that it is ridiculous to say that the corrupted image is much higher in meaningful information than is the original image.

    The pictorial example in Evo-Info 4 illustrates that ASC is not necessarily conserved in the sense that algorithmic mutual information is conserved. The transformation f(x) of the image x results in an image that is identical in dimensions to x: the image f(x) is not the empty string. Furthermore, the probability of f(x) is much less than the probability of x, but is not zero.

    I could have formalized the pictorial example, and used it in a proof. But I chose instead to give a simpler proof of a more-interesting proposition that contradicts “conservation of information” (as explained in the OP).

    =============

    ETA: Suppose you model the mitochondrial DNA in a eukaryotic cell as a binary string, and assign probabilities p(x) to binary strings. You might set p(λ) = 0 for the empty string λ. But if a cell divides, and one of the resulting cells gets none of the mitochondria, then the ASC of the mitochondrial DNA of that cell is infinite. That is, the mitochondrial DNA is represented by the empty string λ, and p(λ) = 0 implies infinite ASC.

  40. EricMH:

    Joe Felsenstein: Neither colewd nor EricMH has provided a proof of that.

    Neither you nor Dr. English seem to have read the Bio-C paper, where said proof is provided.

    I have read the paper and nope, such a proof is not there. Let me quote the sentences from my comment that explain what “that” is:

    Joe Felsenstein:
    ….
    If colewd wants to claim that the conservation of ASC may not be true in general but is true for all biologically realistic cases. he should consider that (1) that’s not what EricMH asserted, and (2) that assertion needs a proof. Neither colewd nor EricMH has provided a proof of that.

    So “that” is the statement that although there may not be conservation of ASC in general, there is conservation in all biologically realistic cases. Your BIO-Complexity paper does not discuss that issue at all.

    I thought that my comment was very clear but it seems to be easy to misread it, so I suppose I should apologize for that.

  41. DNA_Jock: I’ve seen a lot of hand-waving, but no attempt to address the fact that {conservation (non-growth) of Algorithmic MUTUAL Information} does not imply anything about {conservation (non-growth) of algorithmic specified complexity} .
    That’s something of a show-stopper. We’ve seen counter-examples, both in the action of functions on binary strings, and in realistic simulations of biology.

    No, all of that is a red herring. There is no demonstration, empirical or mathematical, that ASC is not conserved, and the conservation has been proven in the Bio-C paper I wrote, and a probabilistic bound proven in Dr. Ewert’s original work. It is impossible to empirically disprove something that is mathematically proven. You should read the Bio-C paper first, and then if you discover a counter example submit it to Bio-C. If you have a legitimate counter example, Bio-C will certainly print your article.

    That being said, Dr. English raised a legitimate problem with ASC in this comment:

    Tom English: There is nothing in the definition of ASC that requires the context C to be used in compressing the binary string x, which is to say that K(x|C) is not necessarily smaller than K(x).

    This is the one legitimate complaint Dr. English raises against ASC being a measure of meaning. If I(x) – K(x) = I(x) – K(x|C), then x doesn’t have a measurable reference to C, yet has a high ASC value. So, in this case, high ASC does not necessarily entail reference to C.

    This is a real shortcoming of ASC that needs to be addressed, but it is a technical flaw rather than a fundamental flaw. One simple approach is to just discard reliance on Kolmogorov complexity, since it is the prefix free description that does all the mathematical heavy lifting in Dr. Ewert’s work, and that doesn’t have any inherent need for Kolmogorov complexity.

    All that being said, this is an entirely separate issue from the conservation debate. That debate is a non-issue, and again I point to the Bio-C paper.

    https://bio-complexity.org/ojs/index.php/main/article/view/BIO-C.2019.2

  42. Tom English,

    ETA: Suppose you model the mitochondrial DNA in a eukaryotic cell as a binary string, and assign probabilities p(x) to binary strings. You might set p(λ) = 0 for the empty string λ. But if a cell divides, and one of the resulting cells gets none of the mitochondria, then the ASC of the mitochondrial DNA of that cell is infinite. That is, the mitochondrial DNA is represented by the empty string λ, and p(λ) = 0 implies infinite ASC.

    Why would this not be undefined vs infinity?

  43. EricMH: If you think there is a problem with my Bio-C paper, or with Dembski’s conservation of information, then you need to submit a criticism to Bio-C.

    I have written extensively on what is wrong with William Dembski’s (2002) argument using the Law of Conservation of Complex Specified Information to show that specifications such as high levels of fitness cannot be achieved by ordinary evolutionary processes. Namely, to establish that, the specification must be held the same before and after the action of evolutionary processes. One is trying to establish that one cannot achieve the specification unless one starts out already having it. ‘Functional Information” arguments have the same structure, with the definition of “function” not changing from before to after.

    However, when using the LCCSI Dembski defines a different specification Before, different from the high-fitness specification, which applies After. Dembski sketches a proof which may well work. So the theorem might be true, but is in a form that is irrelevant to showing that “Specified Complexity Cannot be Purchased Without Intelligence”. At least, not if the state of specified complexity is a state of high fitness or good adaptation.

    I also argued that the 2005 revision of Dembski’s argument changes the null distribution from a mutation-like one which has equal probability on all possible genotypes to a distribution of results from the action of evolutionary processes, including natural selection. No hint is given how to discover that distribution. Dembski’s 2005 argument has become totally silly:
    (1) to show that a state of high fitness cannot be reached by evolutionary processes, we must show that Complex Specified Information exists.
    (2) We define CSI as present only when evolutionary processes cannot produce that state except with unreasonably low probability.
    (3) To show whether CSI is present we then need to first show that evolutionary processes cannot produce the state except with unreasonably low probability.

    Of course this is logically perfect — I cannot argue that it is disproven. Just that it is totally useless and totally silly. CSI is then tacked on only after showing what you wanted, and it adds nothing to the argument. Dembski of course argues that he has not changed his argument since 2002. Which makes things worse for his 2002 argument.

    How the BIO-Complexity paper validates Dembski’s 2002 argument is not explained in the Nemati and Holloway paper.

  44. EricMH: There is no demonstration, empirical or mathematical, that ASC is not conserved, and the conservation has been proven in the Bio-C paper I wrote

    Say what? Your Bio-C paper does not even purport to demonstrate that ASC cannot increase. You work with expected ASC, the biological relevance of which is nil.

    EricMH: It is impossible to empirically disprove something that is mathematically proven.

    What an interesting thing to say. So if reality and Eric’s math disagree, it is reality that needs fixing? Modest cove, aren’t you?

  45. colewd: We know there is new information what we don’t know is the mechanism.

    We do know the mechanism. We’ve explained it you several dozen times before. Why do you continue to ignore the scientifically verified explanation you’ve been provided so many times?

  46. EricMH: It is impossible to empirically disprove something that is mathematically proven.

    It is however entirely possible to empirically disprove a nonsense claim based on a “mathematically proven” thing when the “mathematically proven” thing has no relevance to actual biological reality.

  47. Adapa,

    We do know the mechanism. We’ve explained it you several dozen times before. Why do you continue to ignore the scientifically verified explanation you’ve been provided so many times?

    Are you claiming that natural selection explains the diversity of life?

  48. Joe Felsenstein,

    (1) to show that a state of high fitness cannot be reached by evolutionary processes, we must show that Complex Specified Information exists.
    (2) We define CSI as present only when evolutionary processes cannot produce that state except with unreasonably low probability.

    The argument on Eric/Dembski’s side is not about fitness but about new genetic information. I don’t think anyone will argue that fitness cannot be improved by natural selection. The problem I see evolutionary theory not currently solving is significant new features observed over time. Features that require significant amounts of new functional information. Gpuccio’s article on vertebrate transition is an example.

    The highly engineered transition to vertebrates: an example of functional information analysis

  49. colewd: Are you claiming that natural selection explains the diversity of life?

    You are repeatedly proclaiming that there is some mathematical theorem somewhere saying that information cannot be “created” by natural evolutionary processes. Where is this theorem? The more we ask you to support your claims, the more you seem to go off to trying to divert us with discussion of whether natural selection explains the diversity of life.

    If there is not such a theorem (and there is not such) then it does not follow that automatically natural selection can explain everything. So going from the one to the other is just a diversionary tactic. Cut it out.

    Oh, and if there is a “conservation” theorem preventing increase of genetic information, then it applies whether or not the genetic information is “significant”.

  50. Joe Felsenstein,

    Oh, and if there is a “conservation” theorem preventing increase of genetic information, then it applies whether or not the genetic information is “significant”.

    I believe Eric is claiming that information cannot be increased with an algorithmic process. I consider natural selection to be this type of process. Do you disagree?

Leave a Reply