Evo-Info 4 addendum

Posted on by
Introduction to Evolutionary Informatics, by Robert J. Marks II, the “Charles Darwin of Intelligent Design”; William A. Dembski, the “Isaac Newton of Information Theory”; and Winston Ewert, the “Charles Ingram of Active Information.” World Scientific, 332 pages.
Classification: Engineering mathematics. Engineering analysis. (TA347)
Subjects: Evolutionary computation. Information technology–Mathematics.

In “Evo-Info 4: Non-Conservation of Algorithmic Specified Complexity,” I neglected to explain that algorithmic mutual information is essentially a special case of algorithmic specified complexity. This leads immediately to two important points:

  1. Marks et al. claim that algorithmic specified complexity is a measure of meaning. If this is so, then algorithmic mutual information is also a measure of meaning. Yet no one working in the field of information theory has ever regarded it as such. Thus Marks et al. bear the burden of explaining how they have gotten the interpretation of algorithmic mutual information right, and how everyone else has gotten it wrong.
  2. It should not come as a shock that the “law of information conservation (nongrowth)” for algorithmic mutual information, a special case of algorithmic specified complexity, does not hold for algorithmic specified complexity in general.

My formal demonstration of unbounded growth of algorithmic specified complexity (ASC) in data processing also serves to counter the notion that ASC is a measure of meaning. I did not explain this in Evo-Info 4, and will do so here, suppressing as much mathematical detail as I can. You need to know that a binary string is a finite sequence of 0s and 1s, and that the empty (length-zero) string is denoted \lambda. The particular data processing that I considered was erasure: on input of any binary string x, the output \mathtt{erased}(x) is the empty string. I chose erasure because it rather obviously does not make data more meaningful. However, part of the definition of ASC is an assignment of probabilities to all binary strings. The ASC of a binary string is infinite if and only if its probability is zero. If the empty string is assigned probability zero, and all other binary strings are assigned probabilities greater than zero, then the erasure of a nonempty binary string results in an infinite increase in ASC. In simplified notation, the growth in ASC is

    \[A(\mathtt{erased}(x)) - A(x) = \underbrace{A(\lambda)}_\text{infinite} - \underbrace{A(x)}_\text{finite} = \infty\]

for all nonempty binary strings x. Thus Marks et al. are telling us that erasure of data can produce an infinite increase in meaning.

In Evo-Info 4, I observed that Marks et al. had as “their one and only theorem for algorithmic specified complexity, ‘The probability of obtaining an object exhibiting \alpha bits of ASC is less then [sic] or equal to 2^{-\alpha},’” and showed that it was a special case of a more-general result published in 1995. George Montañez has since dubbed this inequality “conservation of information.” I implore you to understand that it has nothing to do with the “law of information conservation (nongrowth)” that I have addressed.

Now I turn to a technical point. In Evo-Info 4, I derived some theorems, but did not lay them out in “Theorem … Proof …” format. I was trying to make the presentation of formal results somewhat less forbidding. That evidently was a mistake on my part. Some readers have not understood that I gave a rigorous proof that ASC is not conserved in the sense that algorithmic mutual information is conserved. What I had to show was the negation of the following proposition:

(False)   \[A(f(x); c, P) - A(x; c, P) \leq K(f) + O(1) \]

for all binary strings x and c, for all probability distributions P over the binary strings, and for all computable [ETA 12/12/2019: total] functions f on the binary strings. The variables in the proposition are universally quantified, so it takes only a counterexample to prove the negated proposition. I derived a result stronger than required:

Theorem 1. There exist computable function f and probability distribution P over the binary strings such that

    \[A(f(x); c, P) - A(x; c, P) = \infty\]

for all binary strings c and for all nonempty binary strings x.

Proof. The proof idea is given above. See Evo-Info 4 for a rigorous argument.

In the appendix, I formalize and justify the claim that algorithmic mutual information is essentially a special case of algorithmic specified complexity. In this special case, the gain in algorithmic specified complexity resulting from a computable transformation f(x) of the data x is at most K(f) + O(1), i.e., the length of the shortest program implementing the transformation, plus an additive constant.

Appendix

Some of the following is copied from Evo-Info 4. The definitions of algorithmic specified complexity (ASC) and algorithmic mutual information (AMI) are:

    \begin{align*} A(x; c, P) &:= -\!\log P(x) - K(x|c) &\text{(ASC)} \\ I(x: c) &:= K(x) - K(x|c^*), &\text{(AMI)} \\ \end{align*}

where P is a distribution of probability over the set \mathcal{X} := \{0, 1\}^* of binary strings, x and c are binary strings, and binary string c^* is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity K(\cdot) and the conditional algorithmic complexity K(\cdot|\cdot) are defined, outputting c. The base of logarithms is 2. The “law of conservation (nongrowth)” of algorithmic mutual information is:

(1)   \begin{equation*} I(f(x) : c) \leq I(x:c) + K(f) + O(1) \end{equation*}

for all binary strings x and c, and for all computable [ETA 12/12/2019: total] functions f on the binary strings. As shown in Evo-Info 4,

    \[I(x: c) = -\!\log M(x) - K(x|c^*),\]

where the universal semimeasure M on \mathcal{X} is defined M(x) := 2^{-K(x)} for all binary strings x. Here we make use of the normalized universal semimeasure

    \[M^*\!(x) := \frac{M(x)}{M(\mathcal{X})},\]

where M(\mathcal{X}) = \sum_x M(x). Now the algorithmic mutual information of binary strings x and c differs by an additive constant, \log M(\mathcal{X}), from the algorithmic specified complexity of x in the context of c^* with probability distribution M^*.

Theorem 2. Let x and c be binary strings. It holds that

    \[I(x : c) = A(x; c^*\!, M^*) - \log M(\mathcal{X}).\]

Proof. By the foregoing definitions,

    \begin{align*} I(x : c) &= K(x) - K(x|c^*) \\ &= -\!\log M(x) - K(x|c^*) \\ &= -\!\log(M(\mathcal{X}) M^*\!(x)) - K(x|c^*) \\ &= -\!\log M^*\!(x) - K(x|c^*) - \log M(\mathcal{X}) \\ &= A(x; c^*, M^*) - \log M(\mathcal{X}). \end{align*}

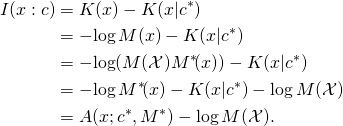
Theorem 3. Let x and c be binary strings, and let f be a computable [and total] function on \mathcal{X}. Then

    \[A(f(x); c^*\!, M^*) - A(x; c^*\!, M^*) \leq K(f) + O(1).\]

Proof. By Theorem 2,

    \begin{align*} &A(f(x); c^*\!, M^*) - A(x; c^*\!, M^*) \\ &\quad = [I(f(x) : c) - \log M^*\!(\mathcal{X})] - [I(x : c) - \log M^*\!(\mathcal{X})] \\ &\quad = I(f(x) : c) - I(x : c) \\ &\quad \leq K(f) + O(1). \\ \end{align*}

The inequality in the last step follows from (1).

153 thoughts on “Evo-Info 4 addendum”

  1. BruceS: If there are any new mathematical ideas in the Montañez paper, even a short post pointing those out would be helpful. However, I suspect that I am the only one at TSZ (except possibly for Keith?) interested in the math for its own sake. So you may not want to both for such a small potential audience.

    That’s a difficult question. But, as Joe said above, what George is doing looks a lot like Neyman-Pearson hypothesis testing, and thus seems not to be new. However, George does not see what he’s doing as comparison of two competing hypotheses. He sees what he’s doing as testing a single hypothesis. I’ll say that if he’s right about that, then he ought to be able to get the hypothesis-testing logic, minus the ID baggage, through peer review at a journal with mathematical statistics as one of its main topics. Bio-Complexity is definitely not the place to get a strong check of his claims.

    As for responding to a small audience, I’ve spent the day posting comments on the other thread, knowing full well that you might be the only person to read them (closely, anyway). Take that to mean that I think well of you.

  2. BruceS: From what I have read of him, Eric has not explicitly made this claim about universal computing, but rather claimed that mathematics dictates the behavior of the universe.

    He has repeatedly equated naturalism with a claim that the universe is Turing-computable. I first saw this in his Alternative Methods to Naturalism (AmNat) talk, “Imagination Sampling.” (I put a lot of work into a post titled “Captain Imagination,” but never finished it. Perhaps there is something salvageable.) There is at least a latent claim, in stuff he’s posted, that nature is a computer running a program, and that the program has to come from somewhere. I’m not going to pore over his old posts, to find support for my impression. Consider also that he says that intelligence literally is a Turing oracle.

  3. Tom English: He has repeatedly equated naturalism with a claim that the universe is Turing-computable.

    I interpret this as saying that Eric believes the laws of physics must be Turing computable. I see three issues in that:
    – what if anything limits laws formed by human intellect
    – what is the metaphysics of laws of nature, eg necessity versus simple regularities
    – how does the universe implement laws; I think computing is different from embodying (eg stomachs don’t compute digestion)

    These issues are philosophical. Eric and I have exchanged ideas on the philosophy of science and I believe it is not something he has studied. So unless Eric wants to get involved, I guess it’s probably not useful to speculate further on his views.

Leave a Reply