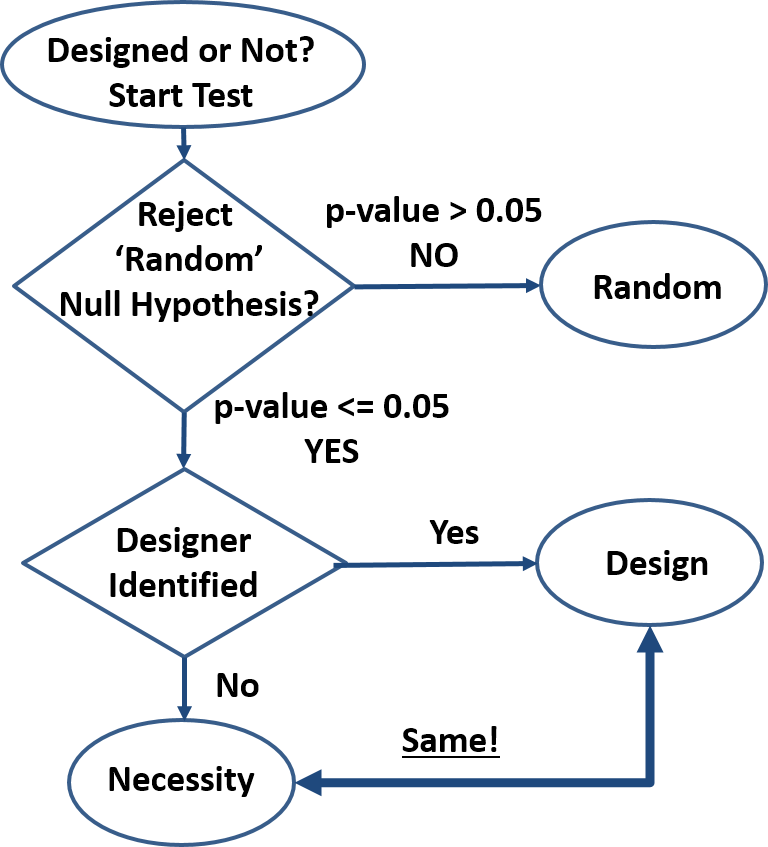
Design is order imposed on parts of a system. The system is designed even if the order created is minimal (e.g. smearing paint on cave walls) and even if it contains random subsystems. ‘Design’ is inferred only for those parts of the system that reveal the order imposed by the designer. For cave art, we can analyze the paint, the shape of the paint smear, the shape of the wall, composition of the wall, etc. Each one of these separate analyses may result in separate ‘designed’ or ‘not designed’ conclusions. The ‘design’-detection algorithm shown in the attached diagram can be employed to analyze any system desired.
- How do we know something is not random? By rejecting the null hypothesis: “the order we see is just an artifact of randomness”. This method is well established and common in many fields of research (first decision block in diagram). If we search for extraterrestrial life, archeological artefacts, geologic events, organic traces, etc., we infer presence based on specific nonrandom patterns. Typical threshold (p-value) is 0.05 meaning “the outcome observed may be due to randomness with a 5% or less probability”. The actual threshold is not critical, as probabilities quickly get extreme. For instance, given a 10-bit outcome (10 coin toss set), the probability of that outcome being random yet matching a predetermined sequence is 0.1%, well below the 5% threshold. A quick glance at biological systems show extreme precision repeated over and over again and indicating essentially zero probability of system-level randomness. Kidneys and all other organs are not random, reproduction is not random, cell structure is not random, behavior is not random, etc.
- Is a nonrandom feature caused by design or by necessity? Once randomness has been excluded, the system analyzed must be either designed as in “created by an intelligent being”, or a product of necessity as in “dictated by the physical/scientific laws”. Currently (second decision block in diagram), a design inference is made when potential human/animal designers can be identified, and a ‘necessity’ inference is made in all other cases, even when there is no known necessity mechanism (no scientific laws responsible). This design detection method is circumstantial hence flawed, and may be improved only if a clearer distinction between design and necessity is possible. For instance, the DNA-to-Protein algorithm can be written into software that all would recognize as designed when presented under any other form than having been observed in a cell. But when revealed that this code has been discovered in a cell, dogmatic allegiances kick in and those so inclined start claiming that this code is not designed despite not being able to identify any alternative ‘necessity’ scenario.
- Design is just a set of ‘laws’, making the design-vs-necessity distinction impossible. Any design is defined by a set of rules (‘laws’) that the creator imposes on the creation. This is true for termite mounds, beaver dams, beehives, and human-anything from pencils to operating systems. Product specifications describe the rules the product must follow to be acceptable to customers, software is a set of behavior rules obeyed, and art is the sum of rules by which we can identify the artist, or at least the master’s style. When we reverse-engineer a product, we try to determine its rules – the same way we reverse-engineer nature to understand the scientific laws. And when new observations infirm the old product laws, we re-write them the same way we re-write the scientific laws when appropriate (e.g. Newton’s laws scope change). Design rules have the same exact properties as scientific laws with the arbitrary distinction that they are expected to be limited in space and time, whereas scientific laws are expected to be universal. For instance, to the laboratory animals, the human designed rules of the laboratory are no different than the scientific laws they experience. Being confined to their environment, they cannot verify the universality of the scientific laws, and neither can we since we are also confined in space and time for the foreseeable future.
- Necessity is Design to the best of our knowledge. We have seen how design creates necessity (a set of ‘laws’). We have never confirmed necessity without a designer. We have seen that the design-necessity distinction is currently arbitrarily based on the identification of a designer of a particular design and on the expectation of universality of the scientific laws (necessity). Finally, we can see that natural designs cannot be explained by the sum of the scientific laws these designs obey. This is true for cosmology (galaxies/stars/planets), to geology (sand dunes/mountains/continents), weather (clouds/climate/hydrology), biology (molecules/cells/tissues/organisms), and any other natural design out there.
- Scientific laws are unknowable. Only instances of these laws are known with any certainty. Mathematics is necessary but insufficient to determine the laws of physics and furthermore the laws of chemistry, biology, behavior, etc., meaning each of the narrower scientific laws has to be backwards compatible with the broader laws but does not derive from the more general laws. Aside from mathematics that do not depend on observations of nature, the ‘eternal’ and ‘universal’ attributes attached to the scientific laws are justified only as simplifying working assumptions, yet too often these are incorrectly taken as indisputable truths. Any confirming observation of a scientific law is nothing more than another instance that reinforces our mental model. But we will never know the actual laws, no matter how many observations we make. Conversely, a single contrary observation is enough to invalidate (or at least shake up) our model as happened historically with many of the scientific laws hypothesized.
- “One Designer” hypothesis is much more parsimonious compared to a sum of disparate and many unknown laws, particles, and “random” events. Since the only confirmed source of regularity (aka rules or laws) in nature is intelligence, it takes a much greater leap of faith to declare design a product of a zoo of laws, particles, and random events than of intelligence. Furthermore, since laws and particles are presumably ‘eternal’ and ‘universal’, randomness would be the only differentiator of designs. But “design by randomness” explanation is utterly inadequate especially in biology where randomness has not shown a capacity to generate design-like features in experiment after experiment. The non-random (how is it possible?) phantasm called “natural selection” fares no better as “natural selection” is not a necessity and in any case would not be a differentiator. Furthermore, complex machines such as the circulatory, digestive, etc. system in many organisms cannot be found in the nonliving with one exception: those designed by humans. So-called “convergent evolution”, the design similarity of supposedly unrelated organisms also confirms the ‘common design’ hypothesis.
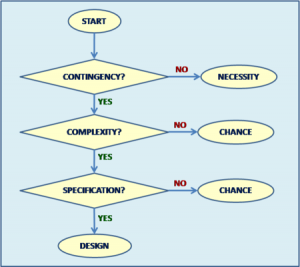
- How does this proposed Intelligent Design Detection Method improve Dembski’s Explanatory Filter? The proposed filter is simpler, uncontroversial
with the likely [important] exception of equating necessity with design, and is not dependent on vague concepts like “complexity”, “specification”, and “contingency”. Attempts to quantify “specified complexity” by estimating ”functional information” help clarify Dembski’s Explanatory Filter, but still fall short because design needs not implement a function (e.g. art) while ‘the function’ is arbitrary as are the ‘target space’, ‘search space’, and ‘threshold’. Furthermore, ID opponents can easily counter the functional information argument with the claim that the ‘functional islands’ are linked by yet unknown, uncreated, eternal and universal scientific laws so that “evolution” jumps from island to island effectively reducing the search space from a ‘vast ocean’ to a manageable size.
Summary
- Design is order imposed on parts of a system
- A system is nonrandom if we reject the null hypothesis: “the order we see is just an artifact of randomness”
- Current design detection method based on identifying the designer is circumstantial hence flawed
- Design is just a set of ‘laws’, making the design-vs-necessity distinction impossible
- Necessity is Design to the best of our knowledge
- Scientific laws are unknowable. Only instances of these laws are known with any certainty
- “One Designer” hypothesis is much more parsimonious compared to a sum of disparate and many unknown laws, particles, and “random” events
- This Intelligent Design Detection Method improves on Dembski’s Explanatory Filter
Pro-Con Notes
Con: Everything is explained by the Big Bang singularity, therefore we don’t need Intelligent Design.
Pro: How can a point of disruption where all our knowledge completely breaks down explain anything? To the best of our knowledge, Intelligent Design is responsible for that singularity and more.
That’s what I mean if/when I say NS is random. Of course, when I say it, I get all sorts of push-back. 🙂
Now, is NS random in the same sense that genetic drift is random?
If I do not know this, if I lack this information, should I bet the dollar or should I not bet the dollar?
There’s a 15% chance that any number will turn up in a draw. So after 1000 draws the expected number of appearances for any number is 150. The Law of the large numbers states that as you increase the number of trials, it converges to 15%. So it’s much more improbable to get number 17 turn up more than 160 times after 1000 draws than > 16 times after 100 draws
Utility functions. How do you value the thrill of winning and the agony of defeat versus a buck.
Please note that where I live, the provincial government got elected promising “a buck a beer”. Would living here affect your utility?
Plus, you did not mention whether you were smart enough to figure out that the government made money so you cannot win, even in the long term, unless you quit while you are ahead, assuming your long term is long enough. Which it might be if you do not buy a beer.
If its Much more improbable than its statistically significant. If its not actually improbable, or statistically insignificant, than it is to be expected.
Sorta. If natural selection is ‘on’ – ie, a selection coefficient has a value outside the effectively neutral zone – it is still random (probabilistic, not equiprobable), because of genetic drift. They are inseparable. Drift is maximal at neutral, but you don’t turn it off when you turn selection on, you just turn it down.
My choice would have been option 5. But it is not necessarily the only rational option. Some folk might get entertainment value out of the excitement of waiting to see whether they won. And that could make one of the other choices rational for such people.
Yeah, pretty much. For example, after 1000 draws the expected value would be 150 (a 15%). The probability that it’s in the 130 – 170 range is quite high, about a 93%, but there are 40 numbers so the probability that some number appeared less than 130 times or more than 170 is very high, about a 95% if I didn’t screw up the math again
Expected in other words.
Yeah. So if someone run the lottery 1000 times and went looking for number frequencies, and found one (say number 3) outside of the 130-170 range, that wouldn’t suggest the lotto was rigged even though the probability that number 3 fell outside of that range is only a 7%. And thats because the probability that some number will not be in the range is very high, it just happened to be number 3. Do you agree?
I think there is a possibility of p-hacking here. Are you interested in P(any number outside that range) P(3 in particular, picked before hand, outside that range).
I think the moral here is that If you use “random” outside of a model to provide a context then you are just asking for misunderstandings. And possibly that is what some posters enjoy doing. Or possibly not. But I’m not sure if those possibilities are randomly distributed among posters.
Again, you are just explaining what the word expected means. If the probability is high, then we would expect it to happen.
The former.
If we picked number 3 beforehand instead, and it was outside of the range I would say that would be somewhat significant statistically, right?
Yes, but I’m trying to get somewhere with my explanation above. So do you agree that it wouldn’t be unexpected to find some number out of the 40 outside of the range despite the fact that for each of them individually the probability is rather low?
The probability that our expectation is correct?
What I agree with is that if you are saying it is expected, then it is expected. Or not unexpected if you prefer to say it that way.
Good one! Thank you for the reminder that the government always has my best interests at heart.
ETA:
There is a definite bias.
Expected value in mathematical terms is not any old value we aren’t surprised by, it’s the probability-weighted average of all possible values – the average from an infinite run, notionally.
The expectation is a formal term in statistics that indicates the value that repeated runs of an experiment are converging upon. Hence the expected number of heads upon 10 flips of a fair coin is 5. This does not mean you should look surprised when you get 6 or 4 heads 🙂
ninja’d :-/
Right, and when I am saying one should be surprised by that? I am saying quite the opposite. Is that hard for you and Allan to recognize that is what I said?
I am saying that if you have an expected value, and the result falls statistically within that range, then why are we calling that unexpected? It has to be the “exact” value to be expected? That’s silly. Its like saying out of ten coin flips we expect 5 heads and 5 tails, and instead we get 6 heads and 4 tails and then claim this is outside the expected value, so some kind of anomaly exists.
phoodoo,
This would be like saying the results showed an unexpected number of heads.
That would of course be erroneous.
Sorry, your previous post already covered the two situations. I missed it.
All they are saying is that mathematicians call that expected value. It’s the mean value. That doesn’t mean it’s to be expected to get that exact value. In the example above, where p=15%, the probability of getting exactly a 15% of the number of draws is very small for large numbers of draws. For 10000 draws the probability of getting the expected value of 1500 is about a 1%
No problem at all, Bruce
Interestingly, the more you repeat a random event, the more the result converges towards the expected value, yet the expected value gets more and more improbable
phoodoo,
The expected value is an actual value, not a range, in mathematics. You are confusing your colloquial understanding of the term. The expected value of a fair die is 3.5. Not any actual number written on any face. The more you roll, the more your mean will approach 3.5.
Tossing a fair coin 9 times, the expected number of Heads is 4.5. As you go to larger and larger odd numbers of tosses, such as 99 or 999 or 9,999 the expected number of Heads (respectively 49.5, 499.5, and 4,999.5) not only is improbable, if you ever get it you should be *very* surprised. And worried.
As expected.
I’m just trying to figure out when I should look surprised. Is it like what Joe says? Should I looked surprised, or worried? Surporried? Worrised?
You misunderstand again. Look up the title of the OP: “design detection”, not “randomness detection”. That would be impossible anyway (think about it how would you detect “randomness”?)
The method is simple: ASSUME null (random) and determine if outcome is consistent with null. If not, the conclusion is “not random”.
In your example, 6,6,4,6,6,1,6,6,6,6, the method clearly shows this sequence is unlikely to be from a fair die, and that’s what you confirmed too. Simple. If you repeat test X times you would see less “6” if fair die, but if the many “6” pattern continues, it becomes even more obvious the die is loaded. Get it?
Wrong. In the first decision block we just try to determine if outcome is consistent with “random”. If not, then conclusion is “necessity/design”.
Oh my goodness, this gets more and more stupid because you guys can’t understand even the simplest phrases.
First off, here is what Timothy actually wrote:
See that Allan? Read it again perhaps. Try reading it 4.5 times exactly maybe.
There is no EXACT number of times that 17 should be expected. And he is not using the “technical term” for “should have” either Allan. Maybe to you, in math “should have” actually means the bean soup is too sour.
And, even if your incorrect assumptions weren’t quite so incorrect, and he meant some value, it is pure bullcock nonsense to say that in the lotto there is a number, ONE NUMBER, of times that 17 is to be expected. And anything that deviates from that is “unexpected”.
Or do you get to play even more humpty dumtpy word bullshit.
Man, its no wonder you guys can’t understand the problems with evolution. You can’t understand sentences.
You’re the one who doesn’t get it
Yes, there is, if by expected one means “in the long run”, or “as the number of runs tends to infinity”
That’s the mean (average), pretty simple statistical concept I would say
I most certainly ***was*** using the phrases “should have” and “significantly” in their technical, statistical sense. After all, this is a statistical issue, and I am qualified in the discipline, so you can expect me to try to be precise and accurate in my use of terms.
And, by the way, for any known sample size, there most definitely ***is*** a single, determinate number for how often 17 should show up.
And further by the way, “And anything that deviates from that is “unexpected””. This is pure, unadultered nonsense. A statistician ***expects*** that will be variability between samples drawn from a process that is based on random activities. The question is: how likely is the observed variability to have arisen from chance alone, or from a bias in the system under study.
From simple sampling theory on a 6 from 40 lottery, we expect (“should have”) the number 17 turn up in 15% of lotteries. If we have 10,000 lotteries, we expect to see 1500 17s in the set of winning results.
But we don’t. From the actual sampling of somewhere around 10,000 actual lotteries, we see a larger number (I forget exactly what). So the question arises – does the actual number vary so much from the expected number that we should reject the assumption of a “fair game” and embrace the assumption that the game is biassed in some way?
To answer this question, we need a formal, standard statistical test. The test actually answers two questions:
1. Do the sample results lead us to reject the null hypothesis (“fair game”)? In other words, how likely is it that this result has arisen by chance?
2. How confident can we be in the answer to Q1 (the confidence level)?
The test is a fairly simple calculation, which compares an actual mean value with a theoretical mean value for a given sample size. The choice of an acceptable confidence level is arbitrary – we might use significance levels of one “sigma” (one standard deviation from the expected mean), two sigma, three sigma and so on (the Higgs boson evidence displayed 5 sigma difference from a random outcome – so there was a 1 in a million chance that the results arose by chance). What significance level we use usually depends on the nature of the data. Since we are dealing with a very well-specified, simple and controlled process, we would probably go for a three sigma standard.
When I did the analysis of the actual lottery results, the test statistic told me that there was indeed a difference between the actual and theoretical values (we knew that already), but the confidence interval on the result was only about 60%.
OK. We have a calculated statistic and its associated confidence level. How do we interpret it? The formal interpretation would be to say “In any repeated sampling of sets of 10,000 lottery results, we would expect at least 40% of samples to have at least this amount of anomaly”. In other words, the result is not “significant”. So we stick with the null hypothesis that the game is fair.
There is a difference between your use of terms such as “should have”, “expect” and “significance” and the way these terms are used in actual statistical analysis. Your colloquial version is precisely why so many people fall for the “lies, damn lies and statistics” bullshit.
You should not bet on any uncertain process until you know the likelihoods of the various outcomes. Casinos the world over rely on people not knowing this basic fact.
Or, alternatively, until you are sure that the buzz you get from betting keeps you off the streets.
phoodoo,
Wind your neck in. I was merely explaining what ‘expected value’ means in probability.
Exactly. The test of significant difference between expectation and the sampled result is sensitive to the size of the sample. Or to put it differently, as you do, the larger the sample size, the smaller the difference that will test as significantly different.
Yes, I think you are correct. But is there a rational way to measure the buzz of betting versus the utility of retaining the money being frittered away? Given how common is the pathology of uncontrollable gambling, I would suggest there is no reliable metric (otherwise there would be support programs based on that metric).
Ohhhh, allright then. When you wake up someday with four heads, you are entitled to look a little surprised, I suppose.
I guess so: Both scenarios involve a stochastic process (what I call random), one involving a fair die (what you call random) and the other a loaded one (what I also call random, but you might not). Clear so far. So where does the design detection come in?
Again, I fail to see why you are disagreeing with me. Isn’t that exactly what I’ve written?
Oh, “should have” now is a technical term that only mathematicians understand the meaning of. And it is an exact number. Ha, that’s funny Timothy. Because I was using the term “term” to mean a magicians rabbit. And I am using the term “rabbit” to mean that which glows like amber. And I am using the term funny to mean absurd, as in the way you are using words.
To claim that there is one and precisely only one number of times 17 should arise in the lotteries is statistical bullshit, I don’t care if you teach the subject. And any number that is not that exact number is not what we “should” see as you put it (not you said “should”, not even expect). So if we should see the number 17 precisely 20114 times in the lotteries you looked at, and instead you saw it 20115 times, you are now claiming you would be right to tell your students 17 came up more than it should have. And now you want your students to make some judgments based on that information.
And if that is the case, I have a suggestion. Sit in a room and read statistics, but don’t teach them to others. Because that is utter utter bullshit, and I don’t mean utter as in udder or as in a cheerleaders baton.
This is hilariously bad. My use of the term “should have” has been the standard form for describing expected outcomes in standardised experiments since the days of Fisher. Your version is, how shall I put this politely, idiosyncratic.
Of course you can re-define the meaning of a word however you choose. But science doesn’t work that way. It depends on there being a common agreement in the scientific community on the meaning of terms. So words like “expect” and “significance” in statistics have specific and agreed meanings. Evidently, from your commentary, you don’t subscribe to those definitions. Fine, and good luck with convincing the community of experimentalists to agree with you.
This comment suggests that you don’t understand the meaning of the term “expectation value”, nor how to calculate it reliably. Sad, but with some effort you can overcome this handicap.
Sorry, but are you brain-dead? The question was not ever “is there a difference between the expected and observed values of the occurence of 17 in the actual lottery samples?” Of course we expect there to be a difference. The question to be answered is: “Is the difference between the observed value and the theoretical value explainable by random chance or by a bias in the underlying system”.
Yes. I wanted the students to examine their prior assumptions about how the Lotto game actually worked to, perhaps, see that some of them might be wrong. As you are.
Thank you for your udderly useless advice.
No, that’s not the question at all, at least its certainly not what I am arguing. You are claiming, are you still going to stand by this claim, that “should have” refers to exactly one and only one number of times you should see the number 17 in your look at the statistics. Is it ONE number, yes or no? Exactly ONE number. And if it is NOT that number, then you can claim the number you found is not what you “should have” found.
Don’t try to change the subject, answer that question.
Yes, that is exactly what I am saying. No subject-changing involved, that is just your armwaving way of refusing to face up to how statistìcs works.
Here are the basics.
1. We have a 6 from 40 game
2. We assume the game is fair
3. From theory, we expect that the number 17 will turn up in 15% of winning lottery sets
4. We know, also from theory, that the larger the set of lottery samples, the less likely it is that 17 will turn up either more often or less often than 15% of the time.
5. Now we go and collect some data from real-world lotteries and we find that 17 rarely turns up at exactly the expected value. That does not surprise us, since neither does the frequency of any other permitted value. That is how randomly-selected samples are expected to behave.
6. But we may want to know whether the observed frequency of occurrence of 17 is in line with what the theory of a fair game predicts, or was it so extremely improbable that we should conclude the game is biassed. So we construct a test
7. In the case of my class, the results of the test said that there was a 40% chance that the result was the result of chance alone
8. Then on the balance of probability, I should assume the underlying game is fair, and the observed result is just a result of normal random variation
You seem to be under the misapprehension that statistics can give you a single, determinate answer to any question based on a single specific example.
It can’t. That isn’t what it is for. Statistics is designed to answer questions in the form of “given what we know about the past, what is likely to happen in the future”.
That is all.
I am under that assumption?? YOU are the one who is claiming that you can expect a number to appear, an EXACT number, and ANY deviation from that number, even if its ONE, can be considered an unexpected result.
So according to this rather warped view, EVERY number must have come up with an unexpected value. Every number should have been “not what it should have been” according to your definition. Not just 17 (did you mention this to the class?) Because there is no way any of the numbers came up exactly as you predicted.
So every number was not what they should have been
I don’t know who you think you are fooling with this wording.
No. You are still getting it wrong.
The theoretical calculation of 17 turning up in a 6 out of 40 lottery is exact. In a theoretical set of 10,000 lotteries, we expect to see 1500 examples of 17 turning up in the set of winning numbers.
When we go and sample an actual set of 10,000 lotteries, do we expect to see exactly 1500 17s? No, we do not. That would be very unlikely.
The only question worth asking is: “is the number of 17s that have actually been observed so far out of alignment with our expected number that we should reject the assumption of a fair game?”
Have you got it yet?
Timothy Timothy, are you trying to play with words again? Are you trying to walk back what you said?
I asked you very plainly, if the result is ONE number different than the expected value, is it justified to call that an unexpected result. Is it justified to call that “not what it should have been”?
I asked you very clearly, and you said that’s right.
Are you walking that back now? Do you want to apologize now?
Those are your words Timothy. Are you changing them now?
Or when you say “Yes, that’s exactly what I am saying”, do you actually mean, “the fish monger is a philanderer”?