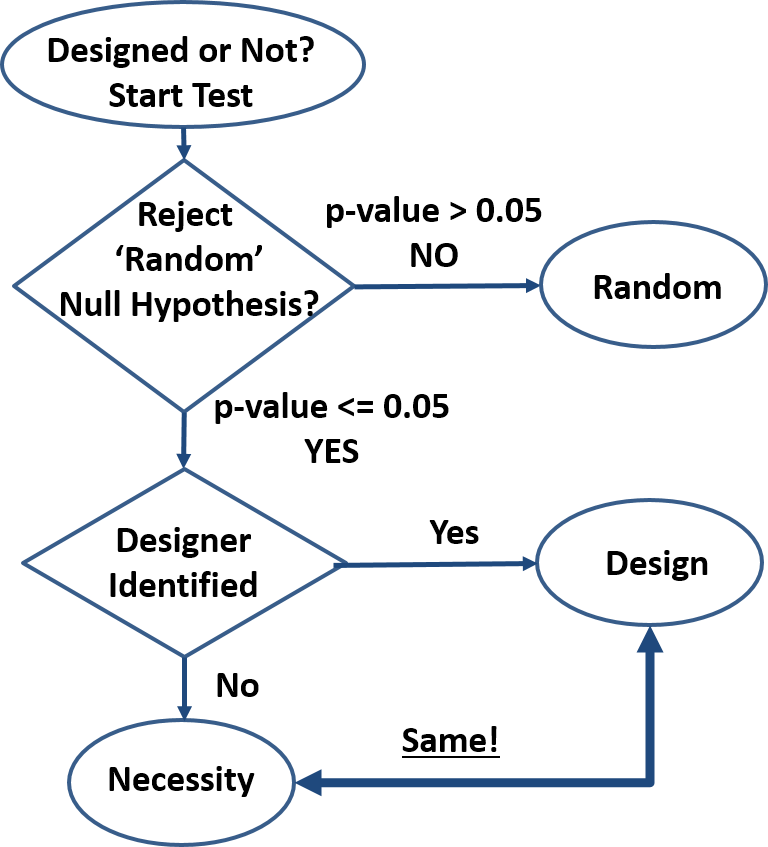
Design is order imposed on parts of a system. The system is designed even if the order created is minimal (e.g. smearing paint on cave walls) and even if it contains random subsystems. ‘Design’ is inferred only for those parts of the system that reveal the order imposed by the designer. For cave art, we can analyze the paint, the shape of the paint smear, the shape of the wall, composition of the wall, etc. Each one of these separate analyses may result in separate ‘designed’ or ‘not designed’ conclusions. The ‘design’-detection algorithm shown in the attached diagram can be employed to analyze any system desired.
- How do we know something is not random? By rejecting the null hypothesis: “the order we see is just an artifact of randomness”. This method is well established and common in many fields of research (first decision block in diagram). If we search for extraterrestrial life, archeological artefacts, geologic events, organic traces, etc., we infer presence based on specific nonrandom patterns. Typical threshold (p-value) is 0.05 meaning “the outcome observed may be due to randomness with a 5% or less probability”. The actual threshold is not critical, as probabilities quickly get extreme. For instance, given a 10-bit outcome (10 coin toss set), the probability of that outcome being random yet matching a predetermined sequence is 0.1%, well below the 5% threshold. A quick glance at biological systems show extreme precision repeated over and over again and indicating essentially zero probability of system-level randomness. Kidneys and all other organs are not random, reproduction is not random, cell structure is not random, behavior is not random, etc.
- Is a nonrandom feature caused by design or by necessity? Once randomness has been excluded, the system analyzed must be either designed as in “created by an intelligent being”, or a product of necessity as in “dictated by the physical/scientific laws”. Currently (second decision block in diagram), a design inference is made when potential human/animal designers can be identified, and a ‘necessity’ inference is made in all other cases, even when there is no known necessity mechanism (no scientific laws responsible). This design detection method is circumstantial hence flawed, and may be improved only if a clearer distinction between design and necessity is possible. For instance, the DNA-to-Protein algorithm can be written into software that all would recognize as designed when presented under any other form than having been observed in a cell. But when revealed that this code has been discovered in a cell, dogmatic allegiances kick in and those so inclined start claiming that this code is not designed despite not being able to identify any alternative ‘necessity’ scenario.
- Design is just a set of ‘laws’, making the design-vs-necessity distinction impossible. Any design is defined by a set of rules (‘laws’) that the creator imposes on the creation. This is true for termite mounds, beaver dams, beehives, and human-anything from pencils to operating systems. Product specifications describe the rules the product must follow to be acceptable to customers, software is a set of behavior rules obeyed, and art is the sum of rules by which we can identify the artist, or at least the master’s style. When we reverse-engineer a product, we try to determine its rules – the same way we reverse-engineer nature to understand the scientific laws. And when new observations infirm the old product laws, we re-write them the same way we re-write the scientific laws when appropriate (e.g. Newton’s laws scope change). Design rules have the same exact properties as scientific laws with the arbitrary distinction that they are expected to be limited in space and time, whereas scientific laws are expected to be universal. For instance, to the laboratory animals, the human designed rules of the laboratory are no different than the scientific laws they experience. Being confined to their environment, they cannot verify the universality of the scientific laws, and neither can we since we are also confined in space and time for the foreseeable future.
- Necessity is Design to the best of our knowledge. We have seen how design creates necessity (a set of ‘laws’). We have never confirmed necessity without a designer. We have seen that the design-necessity distinction is currently arbitrarily based on the identification of a designer of a particular design and on the expectation of universality of the scientific laws (necessity). Finally, we can see that natural designs cannot be explained by the sum of the scientific laws these designs obey. This is true for cosmology (galaxies/stars/planets), to geology (sand dunes/mountains/continents), weather (clouds/climate/hydrology), biology (molecules/cells/tissues/organisms), and any other natural design out there.
- Scientific laws are unknowable. Only instances of these laws are known with any certainty. Mathematics is necessary but insufficient to determine the laws of physics and furthermore the laws of chemistry, biology, behavior, etc., meaning each of the narrower scientific laws has to be backwards compatible with the broader laws but does not derive from the more general laws. Aside from mathematics that do not depend on observations of nature, the ‘eternal’ and ‘universal’ attributes attached to the scientific laws are justified only as simplifying working assumptions, yet too often these are incorrectly taken as indisputable truths. Any confirming observation of a scientific law is nothing more than another instance that reinforces our mental model. But we will never know the actual laws, no matter how many observations we make. Conversely, a single contrary observation is enough to invalidate (or at least shake up) our model as happened historically with many of the scientific laws hypothesized.
- “One Designer” hypothesis is much more parsimonious compared to a sum of disparate and many unknown laws, particles, and “random” events. Since the only confirmed source of regularity (aka rules or laws) in nature is intelligence, it takes a much greater leap of faith to declare design a product of a zoo of laws, particles, and random events than of intelligence. Furthermore, since laws and particles are presumably ‘eternal’ and ‘universal’, randomness would be the only differentiator of designs. But “design by randomness” explanation is utterly inadequate especially in biology where randomness has not shown a capacity to generate design-like features in experiment after experiment. The non-random (how is it possible?) phantasm called “natural selection” fares no better as “natural selection” is not a necessity and in any case would not be a differentiator. Furthermore, complex machines such as the circulatory, digestive, etc. system in many organisms cannot be found in the nonliving with one exception: those designed by humans. So-called “convergent evolution”, the design similarity of supposedly unrelated organisms also confirms the ‘common design’ hypothesis.
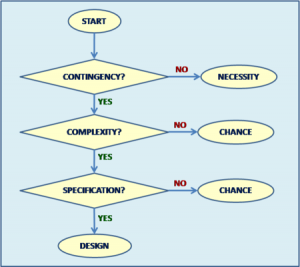
- How does this proposed Intelligent Design Detection Method improve Dembski’s Explanatory Filter? The proposed filter is simpler, uncontroversial
with the likely [important] exception of equating necessity with design, and is not dependent on vague concepts like “complexity”, “specification”, and “contingency”. Attempts to quantify “specified complexity” by estimating ”functional information” help clarify Dembski’s Explanatory Filter, but still fall short because design needs not implement a function (e.g. art) while ‘the function’ is arbitrary as are the ‘target space’, ‘search space’, and ‘threshold’. Furthermore, ID opponents can easily counter the functional information argument with the claim that the ‘functional islands’ are linked by yet unknown, uncreated, eternal and universal scientific laws so that “evolution” jumps from island to island effectively reducing the search space from a ‘vast ocean’ to a manageable size.
Summary
- Design is order imposed on parts of a system
- A system is nonrandom if we reject the null hypothesis: “the order we see is just an artifact of randomness”
- Current design detection method based on identifying the designer is circumstantial hence flawed
- Design is just a set of ‘laws’, making the design-vs-necessity distinction impossible
- Necessity is Design to the best of our knowledge
- Scientific laws are unknowable. Only instances of these laws are known with any certainty
- “One Designer” hypothesis is much more parsimonious compared to a sum of disparate and many unknown laws, particles, and “random” events
- This Intelligent Design Detection Method improves on Dembski’s Explanatory Filter
Pro-Con Notes
Con: Everything is explained by the Big Bang singularity, therefore we don’t need Intelligent Design.
Pro: How can a point of disruption where all our knowledge completely breaks down explain anything? To the best of our knowledge, Intelligent Design is responsible for that singularity and more.
This is so nonsensical as to be almost painful to read. It’s a thought experiment, genius. The premise is that you know how many sides and the layout on the die. And then to get you to make a decision about whether you think the outcome of the rolling of the dice, depending on how they are constructed, qualifies as “random” or not. You are merely being asked a question. What do YOU think would qualify as random? How can you have so many difficulties with this?
I’m curious as to what you mean by that “bias”. Suppose we were concerned about whether there was bias in the selection of, say, recipients of a yearly artistic award. We count how many of the recipients were blue-eyed, and it’s 10%. Then we check the general population from which they came, and it is also 10%.
Does that, in your terms, mean that there is a “bias” toward brown-eyed people?
Because it is germane to the discussion of point #2 in your OP. You think that you can use statistical testing to decide whether a given pattern is random or not. DNA_Jock and me are saying you can’t do that because you lack information on how probable the null-hypothesis and the alternative hypotheses itself are, which is the thing you are really interested in.
Sorry, I fail to see how we are in disagreement about this.
I am fine with that. It’s better than having to defend the notion that 10 billion sixes in a row is extremely implausible, because there is a single non-six in there. “Wow, you got so lucky. a RANDOM sequence of die rolls would never give that result”. Not really.
You don’t have to agree with my rules; I am merely trying to clarify how I use the concept. Nobody is stopping you from calling a draw from a non-uniform distibution “non-random”, but then you would have to reconsider whether natural selection and mutation are truly “random” processes.
Corneel,
You appear to be saying something quite different than Rumraket. If there are 1 billion sides that are a six, and 1 that is a two and you roll ten times and get 9 two’s and 1 six, you can’t conclude this is not random? And if you roll it 100 times, and get 99 twos and 1 six, you still can’t?
If that’s a perfect 1 billion sides die, then the outcome is random by definition. It doesn’t matter what the outcome is. It’s really not that hard to understand
dazz,
Lets see if Corneel agrees with you.
I am? How so?
That is correct, Sir. DNA_Jock explained it twice earlier upthread. What you can conclude is that, given the null-hypothesis that you were using a fair die, both observed outcomes are extremely unlikely. This would lead most people to reject the null-hypothesis that you were using a fair die. What you cannot conclude is that your outcome is not the result of randomness.
Memo to self: never play AD&D with phoodoo.
Yes.
tl;dr
Take a jar filled with red and blue marbles with 66 red marbles and 34 blue marbles. Ask a child to reach into the jar and draw one marble “at random.”
The outcome of the above experiment is biased towards drawing a red marble. There are more red marble than blue marbles. It is more probable, given a random drawing from the jar, that a red marble will be chosen. I hope that clarifies my use of the term.
Yes please. May I have the whole jar?
But Dazz just stated that you know its a fair die. Which are we trying to determine, if its a fair die, or if the results were chosen at random? Given the results we know that one of two possibilities is true. Either it wasn’t a fair die, or it wasn’t chosen at random.
If we know one, we can reject the other. If we know neither it could be both. If we know its a fair die, then we know the results weren’t chosen at random. If we know the results were chosen at random, we know its not a fair die.
I think its pretty straight forward.
No, I just said “if that’s a perfect 1 billion sides die, then the outcome is random by definition”
Which of course should read that we know the probabilities beforehand, by definition
No, even if it’s not a fair die it’s still a random event, only that not all sides are equiprobable
dazz,
My point still stands. We either know something about the process or we know nothing. If we know one then we know the other. If we know nothing at all about the process, we can determine neither. Its either not random or not a fair die, take your pick.
Well, you could simply throw the die multiple times and figure out the probabilities to any level of confidence. Are you saying that there’s no way of knowing anything about random events unless we know the probabilities beforehand?
Do you mean throw them randomly or not randomly?
I’d say that Nonlin was trying to determine the latter. The alternatives (s)he put forward were that a given pattern was ordained by an intelligent agent, or was the result of (deterministic?) necessity. Statistical testing only answers the former question.
BTW: “randomly chosen” sounds like an oxymoron.
..or we witnessed an extremely unlikely event.
So …. does God play dice?
I just mean throw them, and draw conclusions based on the results through well known statistics. Do you think it’s impossible to figure out if a die is fair or not?
And what does random mean to you anyway?
If that is your view, then presumably you would also say that it is “bias” if we elect fewer blue-eyed than brown-eyed senators.
I would say that is not a great usage of the term.
And if you had the same number of red and blue marbles then in Mung’s parlance we could say that it’s biased towards drawing the same number of marbles of both colors. Yawn
But there probably is a bias towards brown-eyed senators. And to remove it we would need people to be biased towards blue-eyed senators. in Minnesota, perhaps there is a bias for blue-eyed artistic reward recipients.
You need to get started rolling that billion sided die and recording the results or we’re going to be here all day.
OK, let’s change the example. We take blood types and find that 10% of senators are type AB and 10% of the population is AB. Is it sensible to then say that there is a bias against electing senators whose blood type is AB? I say that is a poor usage.
A random anecdote about randomness . . .
Many years ago, I taught a class on statistics and used the following example to illustrate the nature of random sampling and cognitive biasing.
In my country, there is a massively popular game of chance called Lotto. You pay your money and choose six numbers out of the set of the first forty integers. Three times a week, some TV celebrity stands in front of a contraption that whirls a set of coloured balls, each one inscribed with one of the forty integers, around in a transparent flask and proceeds to extract six of them (actually the machine does the extraction – the celebrity is just there to attest to the randomness of the process).
The palaver is overseen by three serious-looking people who are referred to in the voiceover as “representatives of The Department of Racing and Gaming”.
If the six extracted numbers match your bet, then you win some enormous amount of money and live happily ever after. Or not, as the case may be. You may recognise this piece of public theatre.
So my scenario for the students was as follows.
The Lotto game has been running for a great many years, so we have a very large set of random samples. We should expect from theory that each of the forty integers will have turned up in the winning sets more or less equally often. But it is not so: the number 17 has turned up more often than it should have (slightly but not significantly more often, but I didn’t tell them that).
Here is a dollar to buy a Lotto ticket. Given the fact about the number 17:
Question 1, do you
1. Deliberately include the number 17 in your bet
2. Deliberately exclude the number 17 from your bet
3. Choose your set of six by some random process
4. Choose your set of six by some non-random process (perhaps the day/month/year numerics of your birthday)
5. Refuse to bet (you get to keep the dollar)
Justify your answer
Question 2:
If I were to continue to give you the price of entry indefinitely into the future, would you go on choosing the same strategy from options 1, 2, 3, 4 or 5 above? If so, why or why not?
Q1: If you’re going to bet, you pick a combination that is unlikely that anyone else picked, to maximize your chances of being the sole winner. Something like 32-33-34-35-36-37. But I would go with option 5, refuse to bet, because the lottery is a tax for dummies.
Q2: I guess there’s a catch somewhere, but I’m going to pick option 5 again for the same reason.
But isn’t this statement to the students by itself not really true? What do you mean more than it should have?
There is no such thing as more than it should right, there is just slightly more than other numbers?
So you are asking them to act on a false premise.
Now if the number 17 really did come up more than it should, say, 96% of the time the number 17 gets picked, the rational about what to do might be different.
dazz,
I would find it interesting to know how often, in all the lotteries around the world, a perfect sequence comes up.
Obviously there are a lot of sequences that have never appeared, but I wonder if 1,2,3,4,5,6 has ever.
When I taught elementary biology many years ago, and was teaching about genetic drift, I once asked a large class this question: “You are tossing a fair coin, and the tosses are independent. You toss 9 times and happen to get 9 Heads. You are about to toss again. What is more likely to happen? (a) It is more likely to be Heads, (b) It is more likely to be Tails, or (c) It is equally likely to be Heads or Tails.”
Many voted for Heads. Their rationale was “You’ve got a run of Heads going”. Few voted for equally likely. A lot of them voted for Tails. Why? Because they had heard that probabilists and statisticians had proven that this was more likely, so that the fraction of Heads would average out to 1/2.
I was astonished that this was how they thought that the laws of probability worked.
Another story: In the 1990s some time I saw a United Airlines Skymall catalog that advertised what was in effect a small plastic Lotto machine. You were urged to buy it to use it to choose Lotto numbers, which would be to your advantage because it used the same method of selecting numbers that the state lotteries used: “random selection”.
That is facepalm territory. I actually kept the catalog and have it somewhere — I should scan that ad and post it.
phoodoo,
In the UK lottery, if 1 2 3 4 5 6 did come up, it would win peanuts. Ten thousand or so people pick it, on the superficially reasonable grounds that it is as likely as any other. Same goes for other runs and biased patterns.
Wrong. It was a brute historical fact that 17 had turned up more often than it should have in what was presumably a fair game. The excess over expectation was real but not statistically significant.
Q1 tested whether the students understood the meaning of sampling independence (as with Joe’s group, the majority did not).
Q2 tested whether they understood the meaning of “the long run”.
Given the purpose of the questions, there was no false premise involved.
Yes, shoot the lottery operators.
Ouch, in that case I guess I was wrong and the best strategy is simply to pick a combination at random, IOW, the best way to maximize your chances of picking a combination that no one else picked is to not even try
Amusingly, major funding for computational evolution has come from lotteries. John Koza, sometimes called the father of genetic programming, came up with the idea for scratch-off lottery tickets, and made a fortune. He has donated 12.7 million USD to the BEACON Center (think Avida) at Michigan State University.
dazz,
Yep. There was one 16 million jackpot that reduced to ‘only’ £100,000 each, because the numbers tended to coincide with the central column on the ticket, hence layout is a source of … bias!
It’s an interesting slant on the ‘random’ aspect. Numbers actually picked by humans tend to favour runs, and/or combinations that favour 1-31 or 1-12. So if you want to maximise payout, avoid those!
But equally, people are bad at picking random numbers. If they try to fake randomness, it can stick out. For example I’ve noticed there is a tendency for consecutive numbers to appear somewhere in winning tickets at least half of the time. It’s probably easy to calculate the probability. But people trying to look random would tend to avoid consecutive numbers. They aren’t ‘random’ enough!
It is a perfectly respectable position to equate ‘random’ with ‘equiprobable’. It is one of the common definitions. But if you do that, you have to concede that Natural Selection is not random.
It is equally respectable to say that ‘random’ just means ‘probabilistic’. On that basis, NS is random.
I think one can tie oneself in knots by being too dogmatic. Imagine the 49 balls of a lottery being differently coloured. One then adds another ball, a different colour to the rest, with ’49’ scrawled on it. If one dismisses the notion than ‘random’ covers all ground except fully-determined, the draw is random with respect to colour, but not random with respect to number. The same draw, the same process, is therefore both.
That’s why I picked 32-33-34-35-36-37, but of course I made the mistake of assuming no one else could possibly follow the same line of reasoning, which must admit, was quite dumb on my part
Tom English,
It’s great to have you back, Tom, hope you’re doing great!
Sheesh Dazz . . .
*** It doesn’t matter what method you use to select your Lotto numbers***.
Random, non-random, patterns in your cat’s food, birthdates, whatever. As I am sure you know, each Lotto draw is an independent, random selection of six numbers from a pool of forty, each of which is equally likely to turn up in any single draw, absent chicanery.
That was the point of my question 1. It doesnt matter which of options 1 to 4 you choose, they each have the same probability of success ***in the next draw***. What mattered was the student’s rationalisation for their choice.
Rationalise option 1 then you have fallen for the “hot-hands” fallacy (wrong, but it doesn’t matter)
Rationalise option 2 then you have fallen for the “regression to the mean in the next draw” fallacy (wrong but it doesn’t matter)
Rationalise option 3 then you are subject to a confused notion that randomness of bet choice equates in some way to the randomness of the actual Lotto draw (wrong but it doesn’t matter)
Rationalise option 4 then you are subject to a confused notion that your birthdate has some special significance (wrong but it doesn’t matter)
There is some justification for options 3 or 4, since they indicate an awareness of sampling independence, which would get a (low) pass mark in my class if rationalised on their face value. If you rationalised options 3 or 4 correctly by saying that they are just ways of generating six appropriate numbers, you would get top marks.
Rationalisations of options 1 or 2 on their face would get a failing mark, even though it doesn’t affect the likelihood of winning the Lotto draw.
Of course, option 5 is the only rational one.
Well actually there is another option: cross out all question 1 options and write “It doesn’t matter how you choose your numbers if you intend to bet”. That would have got the top mark. But nobody in the class did it.
In the context of Q2, the return on investment in Lotto is about 68c return on every dollar invested, so a continuing stream of un-Lottoed dollars will at least pay for a few coffees now and then.
I know that, Tim. My focus was on maximizing my chances of being the sole winner of the price.
Also, I think there’s a case to be made for #1 (Deliberately include the number 17) if you didn’t tell them this…
Because if number 17 turned up significantly more than it should, it could imply that the game is rigged or defective
And, given the enormous pool of people who bet on Lotto, there will be a significant number of people following the same strategy as you suggest, which will frustrate your approach (if they hit on the same 6 numbers as you do and for the same reasons in the same draw, then your prize is halved).
I specifically said that the 17 excess was ***not*** significant (by which I meant statistically significant), only that it existed. If your scenario of “rigged or defective” were considered by the students (which of course they should have), then the only sensible option would be 5 (and they could have explained why in their rationalisation for option 5, or have used it to justify option 1, but nobody didi).
Yes, I already admitted that
I’m confused. You also said you didn’t mention to them whether it was statistically significant or not.
Sorry. I mean that i am saying it to you, but did not say it to them (because at that stage in the course, the term “statistical significance” was ill-defined for them – it was part of the aim of the course to inculcate a proper understanding of the term – hence the question). I simply said to them that there was an excess of 17s, which was true.
Let’s see if I manage to embarrass myself with some math here. Assuming the game is rigged, in the most extreme case the number 17 turns up every time. Picking a combination that includes #17 would multiply your chances of winning by a factor of 40, so ROI would now be 68c times 40 = $27.2
So as long as the 17 ball is 58.8 times more probable of turning up than the rest, ROI is greater than 1 dollar and it would make sense to bet. Does that sound about right?
Well, if I didn’t know that i would argue that we would need to figure it out and how. Perhaps something like modeling the number of appearances of a certain number in N ball draws as a binomial distribution of p=1/40, then calculating a confidence interval for a reasonable value of N to estimate what would count as “statistically significant”
Ahem.
The whole point of Lotto games is that the organiser gets access to that $32c per invested dollar.
Do you imagine that their accountants wouldn’t notice that 17 was turning up every time? And wouldn’t they take steps to prevent the punters from making $27 on every dollar invested?
In any case, you have just reduced the odds from 6 in 40 to 5 in 39 (the odds of getting 17 are now 1.0 but the odds of getting 41 are 0.0). The odds of getting any number between 1 and 40 (excluding 17 are still close to 0.15).
Fuck me, that really was embarrassing, LMAO
I may be wrong
In the case of tossing coins this is a well-known phenomenon: people asked to write down a “random” series of H’s and T’s too rarely allow H to succeed H or T to succeed T. With independent tosses of a fair coin the chance of H being succeeded by H (and of T being succeeded by T) is 1/2. That is true on each toss after the first one, so with 100 tosses the number of times you get the same face of the coin as in the previous toss is a binomial variable with 99 trials and probability 1/2 on each of them. With 100 tosses we then expect 49.5 such successions.
If you ask people to write down a random set of 100 tosses they will tend to switch between heads and tails too often, getting far too few such successions. This of course leads them to see too many “runs of luck” in actual random tosses.
I am confused by this. How can you have an expected number of times you expect to have 17 appear, and then say a number that is larger than that expected number, but not statistically significantly larger?
In other words, its still within the realm of expected. Because we expect things to be within a range which is still statistically insignificant. Otherwise we would call it significant.