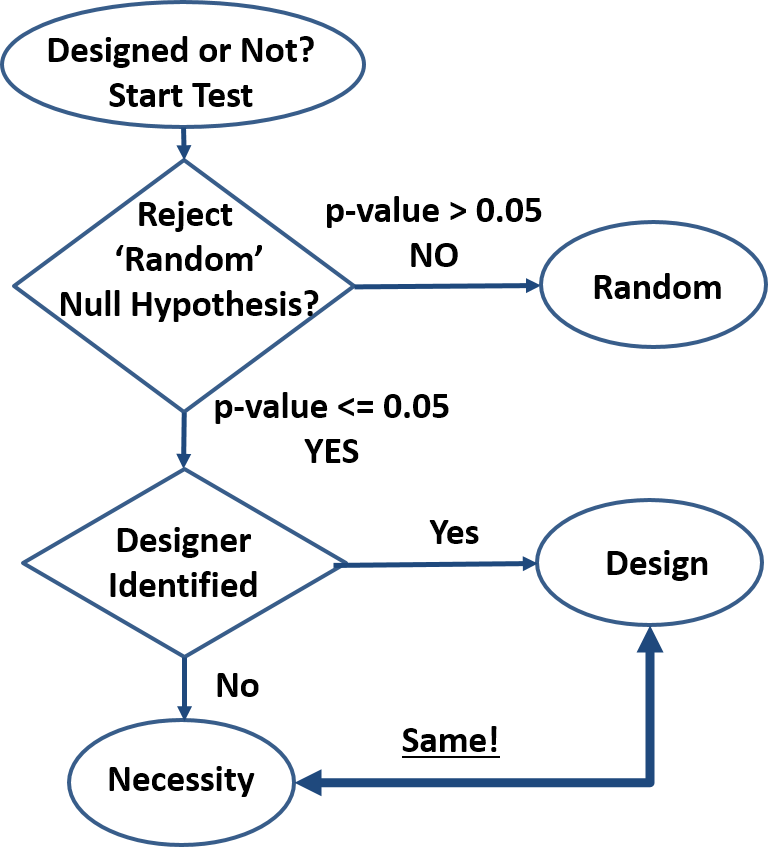
Design is order imposed on parts of a system. The system is designed even if the order created is minimal (e.g. smearing paint on cave walls) and even if it contains random subsystems. ‘Design’ is inferred only for those parts of the system that reveal the order imposed by the designer. For cave art, we can analyze the paint, the shape of the paint smear, the shape of the wall, composition of the wall, etc. Each one of these separate analyses may result in separate ‘designed’ or ‘not designed’ conclusions. The ‘design’-detection algorithm shown in the attached diagram can be employed to analyze any system desired.
- How do we know something is not random? By rejecting the null hypothesis: “the order we see is just an artifact of randomness”. This method is well established and common in many fields of research (first decision block in diagram). If we search for extraterrestrial life, archeological artefacts, geologic events, organic traces, etc., we infer presence based on specific nonrandom patterns. Typical threshold (p-value) is 0.05 meaning “the outcome observed may be due to randomness with a 5% or less probability”. The actual threshold is not critical, as probabilities quickly get extreme. For instance, given a 10-bit outcome (10 coin toss set), the probability of that outcome being random yet matching a predetermined sequence is 0.1%, well below the 5% threshold. A quick glance at biological systems show extreme precision repeated over and over again and indicating essentially zero probability of system-level randomness. Kidneys and all other organs are not random, reproduction is not random, cell structure is not random, behavior is not random, etc.
- Is a nonrandom feature caused by design or by necessity? Once randomness has been excluded, the system analyzed must be either designed as in “created by an intelligent being”, or a product of necessity as in “dictated by the physical/scientific laws”. Currently (second decision block in diagram), a design inference is made when potential human/animal designers can be identified, and a ‘necessity’ inference is made in all other cases, even when there is no known necessity mechanism (no scientific laws responsible). This design detection method is circumstantial hence flawed, and may be improved only if a clearer distinction between design and necessity is possible. For instance, the DNA-to-Protein algorithm can be written into software that all would recognize as designed when presented under any other form than having been observed in a cell. But when revealed that this code has been discovered in a cell, dogmatic allegiances kick in and those so inclined start claiming that this code is not designed despite not being able to identify any alternative ‘necessity’ scenario.
- Design is just a set of ‘laws’, making the design-vs-necessity distinction impossible. Any design is defined by a set of rules (‘laws’) that the creator imposes on the creation. This is true for termite mounds, beaver dams, beehives, and human-anything from pencils to operating systems. Product specifications describe the rules the product must follow to be acceptable to customers, software is a set of behavior rules obeyed, and art is the sum of rules by which we can identify the artist, or at least the master’s style. When we reverse-engineer a product, we try to determine its rules – the same way we reverse-engineer nature to understand the scientific laws. And when new observations infirm the old product laws, we re-write them the same way we re-write the scientific laws when appropriate (e.g. Newton’s laws scope change). Design rules have the same exact properties as scientific laws with the arbitrary distinction that they are expected to be limited in space and time, whereas scientific laws are expected to be universal. For instance, to the laboratory animals, the human designed rules of the laboratory are no different than the scientific laws they experience. Being confined to their environment, they cannot verify the universality of the scientific laws, and neither can we since we are also confined in space and time for the foreseeable future.
- Necessity is Design to the best of our knowledge. We have seen how design creates necessity (a set of ‘laws’). We have never confirmed necessity without a designer. We have seen that the design-necessity distinction is currently arbitrarily based on the identification of a designer of a particular design and on the expectation of universality of the scientific laws (necessity). Finally, we can see that natural designs cannot be explained by the sum of the scientific laws these designs obey. This is true for cosmology (galaxies/stars/planets), to geology (sand dunes/mountains/continents), weather (clouds/climate/hydrology), biology (molecules/cells/tissues/organisms), and any other natural design out there.
- Scientific laws are unknowable. Only instances of these laws are known with any certainty. Mathematics is necessary but insufficient to determine the laws of physics and furthermore the laws of chemistry, biology, behavior, etc., meaning each of the narrower scientific laws has to be backwards compatible with the broader laws but does not derive from the more general laws. Aside from mathematics that do not depend on observations of nature, the ‘eternal’ and ‘universal’ attributes attached to the scientific laws are justified only as simplifying working assumptions, yet too often these are incorrectly taken as indisputable truths. Any confirming observation of a scientific law is nothing more than another instance that reinforces our mental model. But we will never know the actual laws, no matter how many observations we make. Conversely, a single contrary observation is enough to invalidate (or at least shake up) our model as happened historically with many of the scientific laws hypothesized.
- “One Designer” hypothesis is much more parsimonious compared to a sum of disparate and many unknown laws, particles, and “random” events. Since the only confirmed source of regularity (aka rules or laws) in nature is intelligence, it takes a much greater leap of faith to declare design a product of a zoo of laws, particles, and random events than of intelligence. Furthermore, since laws and particles are presumably ‘eternal’ and ‘universal’, randomness would be the only differentiator of designs. But “design by randomness” explanation is utterly inadequate especially in biology where randomness has not shown a capacity to generate design-like features in experiment after experiment. The non-random (how is it possible?) phantasm called “natural selection” fares no better as “natural selection” is not a necessity and in any case would not be a differentiator. Furthermore, complex machines such as the circulatory, digestive, etc. system in many organisms cannot be found in the nonliving with one exception: those designed by humans. So-called “convergent evolution”, the design similarity of supposedly unrelated organisms also confirms the ‘common design’ hypothesis.
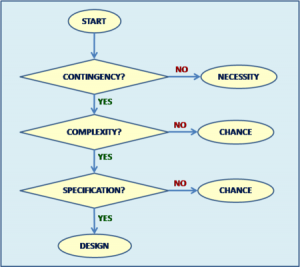
- How does this proposed Intelligent Design Detection Method improve Dembski’s Explanatory Filter? The proposed filter is simpler, uncontroversial
with the likely [important] exception of equating necessity with design, and is not dependent on vague concepts like “complexity”, “specification”, and “contingency”. Attempts to quantify “specified complexity” by estimating ”functional information” help clarify Dembski’s Explanatory Filter, but still fall short because design needs not implement a function (e.g. art) while ‘the function’ is arbitrary as are the ‘target space’, ‘search space’, and ‘threshold’. Furthermore, ID opponents can easily counter the functional information argument with the claim that the ‘functional islands’ are linked by yet unknown, uncreated, eternal and universal scientific laws so that “evolution” jumps from island to island effectively reducing the search space from a ‘vast ocean’ to a manageable size.
Summary
- Design is order imposed on parts of a system
- A system is nonrandom if we reject the null hypothesis: “the order we see is just an artifact of randomness”
- Current design detection method based on identifying the designer is circumstantial hence flawed
- Design is just a set of ‘laws’, making the design-vs-necessity distinction impossible
- Necessity is Design to the best of our knowledge
- Scientific laws are unknowable. Only instances of these laws are known with any certainty
- “One Designer” hypothesis is much more parsimonious compared to a sum of disparate and many unknown laws, particles, and “random” events
- This Intelligent Design Detection Method improves on Dembski’s Explanatory Filter
Pro-Con Notes
Con: Everything is explained by the Big Bang singularity, therefore we don’t need Intelligent Design.
Pro: How can a point of disruption where all our knowledge completely breaks down explain anything? To the best of our knowledge, Intelligent Design is responsible for that singularity and more.
*wince*
Summary: It’s intelligent design because Nonlin says so, and that settles it. At least Nonlin’s honest about that being his unmovable assumption.
That made me cringe too. Interestingly, it’s a mistake that ID-advocates often make…
Very nice OP.
So either it’s “random” (and by random Nonlin seems to suggest that it’s equiprobable in distribution), or it’s designed. LOL.
Under that schematic, the fact that rain falls down, instead of going in every possible direct with equal probability, must be due to design. Gravity? Nah, invisible pixies are carrying each molecule of water down, because gravity must be designed or something to that effect.
Rumraket,
Yep. I’m absolutely convinced by the devastating logic and heading to the closest church. I wonder if there’s a Church of The Rain Pixies though.
I think I can simplify it further such that everything comes out DESIGN.
For we already know that humans can make things appear to be random when in fact they are designed, so if you see randomness, the best inference is to design.
At least Nonlin has abandoned the idea that we infer the existence of a designer from the fact of design, but rather the opposite — if there is an identifiable designer, then the non-random pattern is due to design, and if not, then it is due to necessity.
(Here I’m only using the terms “randomness,” “necessity,” and “design” as implicitly defined by design theorists. I don’t endorse those definitions of those terms, insofar as I understand them at all.)
Welp, I’m convinced. It’s been fun guys.
Sorry, are you reading that differently than:
“In technical terms, a P value is the probability of obtaining an effect at least as extreme as the one in your sample data, assuming the truth of the null hypothesis” ?
http://blog.minitab.com/blog/adventures-in-statistics-2/how-to-correctly-interpret-p-values
Hey, this was supposed to be the noncontroversial part. 🙂 Are you disagreeing with hypothesis testing or just with grammar?
Like I said, Gravity is not a given, but something to be explained. Best inference is that it’s a law given by a Law Maker.
You’re joking, but in fact telling the truth. However, that’s too strong of a statement based on logic and observations. Either way, you can take to the bank the fact that your DNA is NOT RANDOM.
Huh? You misunderstand – read again. I am saying that “a design inference is made when potential human/animal designers can be identified” – not by me, but as standard procedure. I also say that “This design detection method is circumstantial hence flawed”.
Nonlin:
Corneel (& DNA_Jock)
Nonlin:
Your first statement is saying that the probability that the null/random hypothesis is correct, given the outcome observed, is 5% or less. Specifically, you are assigning a probability to the cause “randomness”. Which is really obvious from your next sentence “For instance, given a 10-bit outcome (10 coin toss set), the probability of that outcome being random yet matching a predetermined sequence is 0.1%, well below the 5% threshold.”
Your second attempt “In technical terms…” is, of course, correct. Everything preceding it is utter rubbish.
Can you not see the difference between the two statements? Equating them is a famous Schoolboy Howler.
P(null is true | result) =/= P(result | null is true)
I fully agree with everything DNA_Jock wrote.
So just to pile on: the key phrase is “assuming the truth of the null hypothesis”. Low p-values usually are taken to mean that you were trying to fit an inappropriate null-hypothesis. After all, the observed outcome is unlikely to happen under your hypothesis. But the p-value pertains to the probability of the outcome given the hypothesis, not to the null-hypothesis itself being true.
I never made that mistake in school. But then, I didn’t get very far in school either.
Thanks for the input. You ARE arguing grammar, but I will change for clarity.
How could I say ” the probability that the null/random hypothesis is correct, given the outcome observed” when I emphatically argue that “randomness is unknowable from the outcome”?
Don’t you mean “High p-values”?
How does this revision sound:
“Typical threshold (p-value) is 0.05 meaning “were the outcome observed due to randomness, it would only be observed in 5% or less of trials”. The actual threshold is not critical, as probabilities quickly get extreme. For instance, given a 10-bit outcome (10 coin toss set), the probability of that outcome being random yet matching a predetermined sequence is 0.1%, well below the 5% threshold. ”
I know you don’t mean it, but thanks for you help anyway.
The example should be pretty clear: set a sequence (say HHHTTTHHTT) and do the coin toss x times. If random, one should get that sequence in 0.1% of the cases. Well below the 5% threshold that rejects the null hypothesis.
Anything else? I can’t believe this is the only objection to the whole OP.
Ack! You are still doing it!
Your first sentence is strangely worded, but accurate. The metric here is P(result|null), that is, the probability of getting a result this weird (or weirder), if there is no real difference, just random sampling. Your second sentence is a highly context-dependent assertion. Your third sentence is completely and utterly wrong, because you have switched to talking about P(null|result), that is the probability that the outcome is the result of “randomness’ given the observed result. This is a completely different thing.
And the difference is what Bayes Law is all about.
Hint: your third sentence should read “Given a fair coin fairly tossed, the probability of the outcome is ~0.1%”, not “the probability of that outcome being random”. You are assigning a probability to the (random) cause; you don’t have enough information to do that.
Learn. High. School. Math.
Here’s an example.
I have developed a diagnostic test that is 99% accurate, specifically:
If you have the disease, then P(+) = 0.99, P(-) = 0.01.
If you don’t have the disease, then P(+) = 0.01, P(-) = 0.99
Your doctor administers this test to you. You get a positive result. What is the probability that you have the disease?
Answer: you don’t know.
You know P(+|D), but you want to know P(D|+).
You need more information…
P.S. Your entire OP is gibberish, but this mistake is the first one we need to fix…
You didn’t read the whole thing: “the probability of that outcome being random yet matching a predetermined sequence“. “Outcome being random” is H0 and “matching a predetermined sequence” is the outcome. Agree, it is confusing and needs to be rephrased.
This should work:
“Typical threshold (p-value) is 0.05 meaning “if the outcome were due to randomness (null), it would only be observed in 5% or less of trials”. To reject the “randomness” hypothesis, the actual threshold is not critical, as probabilities get extreme quickly. For instance, given a 10 coin toss set, the probability of that set matching a predetermined sequence given a fair coin is 0.1%, well below the 5% threshold.”
They did not cover this in my high school math classes. But then, I graduated early, I had enough credits before my senior year, so perhaps I missed it.
What odds are you offering?
Nope. Low p-values; low probabilities of observing the outcome under the given null-hypothesis.
As for your exchange with DNA_Jock, let’s try this example:
Suppose I get myself a loaded six-sided die that comes up “6” 80% of the times (I love practical jokes). I keep this fact a secret from you, and cast it ten times in a row in your presence. I get:
6,6,4,6,6,1,6,6,6,6
Looks perfectly fine for a loaded die. Then I ask you whether this is a “random” outcome (which it is). You do your math, and find the chance of getting this number of sixes with a fair die is very small (much smaller than 5%), so you’d say “NO WAY!”.
And you’d be wrong, because you didn’t know your null-hypothesis was wrong: you didn’t know what “random” outcomes were expected!
So you get to reject your null hypothesis (this cannot be the outcome of a fair die, Corneel is playing pranks on me), but you cannot reject “randomness” (HALLELUJAH, IT’S A DESIGNED MIRACLE!).
That’s a pretty funny use of the word random isn’t it?
This is the reason why we keep talking past each other. Here are some possible outcomes of my loaded die:
6 6 3 6 6 1 6 6 6 6
6 6 3 6 6 6 5 6 6 4
6 3 6 2 6 6 6 6 6 6
6 6 6 6 6 6 6 6 6 6
6 2 6 4 6 6 6 6 6 6
Yet, I got 6,6,4,6,6,1,6,6,6,6 by pure chance. Would you say it is not random just because my die is loaded?
Now, would you like to attend church with me next Sunday?
I like the way you put this. I am going to have to remember your example. It brings up the question of what is the difference between “random” and “equiprobable.”
I’d like to see it extended to random genetic drift. Because if people accept that random genetic drift is “random” then they should accept the argument you made.
What is the die only had 6’s on them, would you still call that random if they came up all 6s?
Mmm, that’s interesting. Not sure whether the “random” in random genetic drift refers to the stochastic sampling process or to the alleles having an equal probability of being transmitted (no selection).
Will get back on that.
If I were to go north on the north pole, where would I end up?
ETA: But if the die wouldn’t come up all sixes, I would condede that is a pretty neat trick.
I am not sure if this is supposed to be some kind of coded answer. Would you still call it random or not?
What if its a 1000 sided dice, and only one side is not 6? What if its a billion sided dice, but there is still one side that is not a 6? A trillion?
If there is only a single possible outcome then the whole concept of “random” does not apply, was what I was trying to say.
When there is a slim chance of getting “not-six” then, yes, ten sixes in a row is just one possible outcome of a random draw (though not really a fair draw, I agree).
But I am happy to see that you are warming up to the idea that random and equiprobable are not synonyms.
Another way of picturing random outcomes that are not equiprobable is a roulette wheel where the slots are of different size. Example of equiprobable is 36 slots of 10° slices, but not equiprobable if some slots are, say, 20° and some 5° (or any other way of slicing up the wheel into unequal slots).
There is this urban myth about a guy that spends all day watching a roulette wheel in a casino and noting down the winning numbers. Then, he would start betting on the numbers that were underrepresented and he would win because those numbers would eventually “even up”.
When I heard that story, I said to myself: “That is exactly the wrong way around”.
Don’t give me that. I am due to win the lottery any day now. I’ve been keeping track of the numbers that have not come up.
So as i understand it, from generation to generation the alleles will not have an equal probability. The probability distribution changes as an allele becomes more or less probable given it’s frequency in the population. So the “selection” will continue to be “random” but biased towards alleles that are more numerous.
That is correct: The chance of drawing an allele from the gamete pool is equal to its frequency. Hence the more numerous it is, the greater the chance of drawing it. But each individual gene copy has an equal chance of being transmitted, so I would not call that a bias.
My trusty copy of Hartl & Clark speaks thusly (Principles of Population Genetics 4th ed. p 95):
That reads as if “random” refers both to the sampling process and the absence of selection. Hm, that’s not really satisfactory, is it?
How about “selection is biased towards fitter alleles and fixation towards more numerous alleles”?
Fancy an M&M?
You’re not making any sense. H0 would be that “it’s a fair die” and it would be rightfully rejected. And there’s no guarantee that this method (which I have not invented) is ALWAYS RIGHT. Your samples-size may also be too small. I said very clearly that “probabilities get extreme quickly”, but maybe not that quickly. There’s a procedure to determine the minimum sample size for a valid analysis.
What is your point anyway? are you disputing this well established and common method used daily in many fields of research?
Why don’t you try to find fault elsewhere in the OP? Criticize my logic, not a standard procedure that I merely cite 🙂
Wrong. A low p-value is taken to indicate evidence against the particular hypothesis: https://blog.minitab.com/blog/adventures-in-statistics-2/how-to-correctly-interpret-p-values
He’s making total sense. You’re just not understanding the difference between the two questions:
Is it a fair die?
Is the outcome of the tosses random?
He’s trying to get you to think about the meaning of the word random.
Looks like Mung keeps trying hard to twist the meaning of randomness in the context of evolution to preserve the stupid random-vs-design false dichotomy. I don’t think it’s too hard to get the basic idea: selection isn’t random in the sense that mutations are, namely, that they are independent of (uncorrelated to?) fitness and with no foresight. Selection is stochastic but non-random in that sense, since it biases evolution towards increased fitness.
So it seems to me that evolutionary processes, as a combination of mutation, drift & selection must be unpredictable but non random, IOW, you won’t get the same result twice (mutations/drift) but it will tend to produce fitter populations
Am I missing something?
Now that we fixed grammar (yes?) let’s focus on this: “To reject the “randomness” hypothesis, the actual threshold is not critical, as probabilities get extreme quickly”. Why would you think this is ” highly context-dependent”?
And what about the rest of the OP?
No. You two guys are confused. This OP shows how to identify ‘design’, not ‘random’. That would be an impossible task as explained.
Why would you critique when you don’t even read for comprehension: “The system is designed even if the order created is minimal (e.g. smearing paint on cave walls) and even if it contains random subsystems”?
Yes. Everything. And you asked for it 🙂
I’ll wait for the input of someone who wasn’t homeschooled by his uncle dad, thank you
Well, then you have to defend the notion, that if you get 10 billion sixes in a row, it still could be random, because there could be one non-six in there somewhere.
So if we play by your rules, you will never ever ever know if it is “random” as you call it. I don’t think one has to agree with your rules.
In your neck of the woods? Good luck.