Subjects: Evolutionary computation. Information technology–Mathematics.
The greatest story ever told by activists in the intelligent design (ID) socio-political movement was that William Dembski had proved the Law of Conservation of Information, where the information was of a kind called specified complexity. The fact of the matter is that Dembski did not supply a proof, but instead sketched an ostensible proof, in No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002). He did not go on to publish the proof elsewhere, and the reason is obvious in hindsight: he never had a proof. In “Specification: The Pattern that Signifies Intelligence” (2005), Dembski instead radically altered his definition of specified complexity, and said nothing about conservation. In “Life’s Conservation Law: Why Darwinian Evolution Cannot Create Biological Information” (2010; preprint 2008), Dembski and Marks attached the term Law of Conservation of Information to claims about a newly defined quantity, active information, and gave no indication that Dembski had used the term previously. In Introduction to Evolutionary Informatics, Marks, Dembski, and Ewert address specified complexity only in an isolated chapter, “Measuring Meaning: Algorithmic Specified Complexity,” and do not claim that it is conserved. From the vantage of 2018, it is plain to see that Dembski erred in his claims about conservation of specified complexity, and later neglected to explain that he had abandoned them.
Algorithmic specified complexity is a special form of specified complexity as Dembski defined it in 2005, not as he defined it in earlier years. Yet Marks et al. have cited only Dembski’s earlier publications. They perhaps do not care to draw attention to the fact that Dembski developed his “new and improved” specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. That’s obviously quite different from their current presentation of algorithmic specified complexity as a measure of meaning. Ironically, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then [sic] or equal to
bits of ASC is less then [sic] or equal to ![]() ” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
Lately, a third-wave ID proponent by the name of Eric Holloway has spewed mathematicalistic nonsense about the relationship of specified complexity to algorithmic mutual information. [Note: Eric has since joined us in The Skeptical Zone, and I sincerely hope to see that he responds to challenges by making better sense than he has previously.] In particular, he has claimed that a conservation law for the latter applies to the former. Given his confidence in himself, and the arcaneness of the subject matter, most people will find it hard to rule out the possibility that he has found a conservation law for specified complexity. My response, recorded in the next section of this post, is to do some mathematical investigation of how algorithmic specified complexity relates to algorithmic mutual information. It turns out that a demonstration of non-conservation serves also as an illustration of the senselessness of regarding algorithmic specified complexity as a measure of meaning.
Let’s begin by relating some of the main ideas to pictures. The most basic notion of nongrowth of algorithmic information is that if you input data ![]() to computer program
to computer program ![]() then the amount of algorithmic information in the output data
then the amount of algorithmic information in the output data ![]() is no greater than the amounts of algorithmic information in input data
is no greater than the amounts of algorithmic information in input data ![]() and program
and program ![]() added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image
added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image ![]() by a program
by a program ![]() that is very low in algorithmic information. At left is the input
that is very low in algorithmic information. At left is the input ![]() and at right is the output
and at right is the output ![]() of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the
of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the ![]() -th RGB value of Signature of the Id is the sum of the first
-th RGB value of Signature of the Id is the sum of the first ![]() RGB values of Fuji Affects the Weather.
RGB values of Fuji Affects the Weather.
What is most remarkable about the increase in “meaning,” i.e., algorithmic specified complexity, is that there actually is loss of information in the data processing. The loss is easy to recognize if you understand that RGB values are 8-bit quantities, and that the sum of two of them is generally a 9-bit quantity, e.g.,
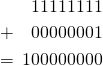
The program ![]() discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image
discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image ![]() from the output image
from the output image ![]() you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
An important detail, which I cannot suppress any longer, is that the algorithmic specified complexity is calculated with respect to binary data called the context. In the calculations above, I have taken the context to be the digital image Fuji. That is, a copy of Fuji has 13 megabits of algorithmic specified complexity in the context of Fuji, and an algorithmically simple corruption of Fuji has 24 megabits of algorithmic specified complexity in the context of Fuji. As in Evo-Info 2, I have used the methods of Ewert, Dembski, and Marks, “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” (2015). My work is recorded in a computational notebook that I will share with you in Evo-Info 5. In the meantime, any programmer who knows how to use an image-processing library can easily replicate my results. (Steps: Convert fuji.png to RGB format; save the cumulative sum of the RGB values, taken in row-major order, as signature.png; then subtract 0.5 Mb from the sizes of fuji.png and signature.png.)
As for the definition of algorithmic specified complexity, it is easiest to understand when expressed as a log-ratio of probabilities,
![]()
where ![]() and
and ![]() are binary strings (finite sequences of 0s and 1s), and
are binary strings (finite sequences of 0s and 1s), and ![]() and
and ![]() are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above,
are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above, ![]() is the probability that a randomly selected computer program converts the context
is the probability that a randomly selected computer program converts the context ![]() into the image
into the image ![]() and
and ![]() is the probability that image
is the probability that image ![]() is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of
is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of ![]() arising by an algorithmic process that depends on the context, and of
arising by an algorithmic process that depends on the context, and of ![]() arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that
arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() and as an alternative hypothesis the proposition that
and as an alternative hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of
then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of ![]() The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level
The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level ![]() when
when ![]()
What we should make of the high algorithmic specified complexity of the images above is that they both are more likely to derive from the context than to arise in the default image-generating process. Again, Fuji is just a copy of the context, and Signature is an algorithmically simple corruption of the context. The probability of randomly selecting a program that cumulatively sums the RGB values of the context is much greater than the probability of generating the image Signature directly, i.e., without use of the context. So we confidently reject the null hypothesis that Signature arose directly in favor of the alternative hypothesis that Signature derives from the context.
This embarrassment of Marks et al. is ultimately their own doing, not mine. It is they who buried the true story of Dembski’s (2005) redevelopment of specified complexity in terms of statistical hypothesis testing, and replaced it with a fanciful account of specified complexity as a measure of meaningful information. It is they who neglected to report that their theorem has nothing to do with meaning, and everything to do with hypothesis testing. It is they who sought out examples to support, rather than to refute, their claims about meaningful information.
Algorithmic specified complexity versus algorithmic mutual information
This section assumes familiarity with the basics of algorithmic information theory.
Objective. Reduce the difference in the expressions of algorithmic specified complexity and algorithmic mutual information, and provide some insight into the relation of the former, which is unfamiliar, to the latter, which is well understood.
Here are the definitions of algorithmic specified complexity (ASC) and algorithmic mutual information (AMI):
![]()
where ![]() is a distribution of probability over the set
is a distribution of probability over the set ![]() of binary strings,
of binary strings, ![]() and
and ![]() are binary strings, and binary string
are binary strings, and binary string ![]() is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity
is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity ![]() and the conditional algorithmic complexity
and the conditional algorithmic complexity ![]() are defined, outputting
are defined, outputting ![]() The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of
The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of ![]() in the context of
in the context of ![]()
The law of conservation (nongrowth) of algorithmic mutual information is:
![]()
for all binary strings ![]() and
and ![]() and for all computable [ETA 12/12/2019: total] functions
and for all computable [ETA 12/12/2019: total] functions ![]() on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability
on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability ![]() where
where ![]() is the empty string, and let
is the empty string, and let ![]() be positive for all nonempty binary strings
be positive for all nonempty binary strings ![]() Also let
Also let ![]() for all binary strings
for all binary strings ![]() Then for all nonempty binary strings
Then for all nonempty binary strings ![]() and for all binary strings
and for all binary strings ![]()
![]()
because
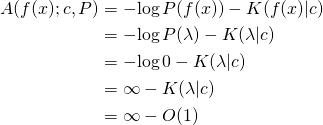
is infinite and ![]() is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that
is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that ![]() is finite for all binary strings
is finite for all binary strings ![]() and
and ![]() I have added a line at the end of the equation to indicate that
I have added a line at the end of the equation to indicate that ![]() is not only finite, but also constant.] Note that this argument can be modified by setting
is not only finite, but also constant.] Note that this argument can be modified by setting ![]() to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing
to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing ![]() can be made arbitrarily large, though not infinite.
can be made arbitrarily large, though not infinite.
There’s a simple way to deal with the different subexpressions ![]() and
and ![]() in the definitions of ASC and AMI, and that is to restrict our attention to the case of
in the definitions of ASC and AMI, and that is to restrict our attention to the case of ![]() in which the context is a shortest program outputting
in which the context is a shortest program outputting ![]()
![]()
This is not an onerous restriction, because there is for every string ![]() a shortest program
a shortest program ![]() that outputs
that outputs ![]() In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as
In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as ![]() We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
![]()
However, the older definition comes with some disadvantages, and I don’t see a significant advantage in using it. Perhaps you will see something that I have not.
The difference in algorithmic mutual information and algorithmic specified complexity,
![]()
has no lower bound, because ![]() is non-negative for all
is non-negative for all ![]() and
and ![]() is negatively infinite for all
is negatively infinite for all ![]() such that
such that ![]() is zero. It is helpful, in the following, to keep in mind the possibility that
is zero. It is helpful, in the following, to keep in mind the possibility that ![]() for a string
for a string ![]() with very high algorithmic complexity, and that
with very high algorithmic complexity, and that ![]() for all strings
for all strings ![]() Then the absolute difference in
Then the absolute difference in ![]() and
and ![]() [added 11/11/2019: the latter expression should be
[added 11/11/2019: the latter expression should be ![]() ] is infinite for all
] is infinite for all ![]() and very large, though finite, for
and very large, though finite, for ![]() There is no limit on the difference for
There is no limit on the difference for ![]() Were Marks et al. to add a requirement that
Were Marks et al. to add a requirement that ![]() be positive for all
be positive for all ![]() we still would be able, with an appropriate definition of
we still would be able, with an appropriate definition of ![]() to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all
to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all ![]()
The remaining difference in the expressions of ASC and AMI is in the terms ![]() and
and ![]() The easy way to reduce the difference is to convert the algorithmic complexity
The easy way to reduce the difference is to convert the algorithmic complexity ![]() into an expression of log-improbability,
into an expression of log-improbability, ![]() where
where
![]()
for all binary strings ![]() An elementary result of algorithmic information theory is that the probability function
An elementary result of algorithmic information theory is that the probability function ![]() satisfies the definition of a semimeasure, meaning that
satisfies the definition of a semimeasure, meaning that ![]() In fact,
In fact, ![]() is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
![]()
that ![]() is a measure, and that
is a measure, and that ![]() is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made
is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made ![]() a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
This does nothing but to establish clearly a sense in which algorithmic specified complexity is formally similar to algorithmic mutual information. As explained above, there can be arbitrarily large differences in the two quantities. However, if we consider averages of the quantities over all strings ![]() holding
holding ![]() constant, then we obtain an interesting result. Let random variable
constant, then we obtain an interesting result. Let random variable ![]() take values in
take values in ![]() with probability distribution
with probability distribution ![]() Then the expected difference of AMI and ASC is
Then the expected difference of AMI and ASC is
![Rendered by QuickLaTeX.com \begin{align*} E[I(X : c) - A(X; c^*\!, P)] &= E[K(X) + \log P(X)] \\ &= E[K(X)] - E[-\!\log P(X)] \\ &= E[K(X)] - H(P). \end{align*}](http://theskepticalzone.com/wp/wp-content/ql-cache/quicklatex.com-318f3c5b560e1b1e12090c6f7bfdfa71_l3.png)
Introducing a requirement that function ![]() be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
![]()
Note that the algorithmic complexity of computable probability distribution ![]() is the length of the shortest program that, on input of binary string
is the length of the shortest program that, on input of binary string ![]() and number
and number ![]() (i.e., a binary string interpreted as a non-negative integer), outputs
(i.e., a binary string interpreted as a non-negative integer), outputs ![]() with
with ![]() bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
![]()
How much the expected value of the AMI may exceed the expected value of the ASC depends on the length of the shortest program for computing ![]()
[Edit 10/30/2019: In the preceding box, there were three instances of ![]() that should have been
that should have been ![]() ] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If
] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If ![]() is computable, then for all binary strings
is computable, then for all binary strings ![]() and
and ![]()
(MDL) 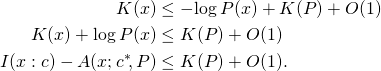
Replacing string ![]() in this inequality with a string-valued random variable
in this inequality with a string-valued random variable ![]() as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
Finally, we express ![]() in terms of the universal conditional semimeasure,
in terms of the universal conditional semimeasure,
![]()
Now ![]() and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that
and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that ![]()
![]()
where ![]() is a distribution of probability over the binary strings
is a distribution of probability over the binary strings ![]() and
and ![]() is the universal conditional semimeasure.
is the universal conditional semimeasure.
An old proof that high ASC is rare
Marks et al. have fostered a great deal of confusion, citing Dembski’s earlier writings containing the term specified complexity — most notably, No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002) — as though algorithmic specified complexity originated in them. The fact of the matter is that Dembski radically changed his approach, but not the term specified complexity, in “Specification: The Pattern that Signifies Intelligence” (2005). Algorithmic specified complexity derives from the 2005 paper, not Dembski’s earlier work. As it happens, the paper has received quite a bit of attention in The Skeptical Zone. See, especially, Elizabeth Liddle’s “The eleP(T|H)ant in the room” (2013).
Marks et al. furthermore have neglected to mention that Dembski developed the 2005 precursor (more general form) of algorithmic specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. Amusingly, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then or equal to
bits of ASC is less then or equal to ![]() ” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
According to the abstract of Milosavljević’s article:
We explore applicability of algorithmic mutual information as a tool for discovering dependencies in biology. In order to determine significance of discovered dependencies, we extend the newly proposed algorithmic significance method. The main theorem of the extended method states that
bits of algorithmic mutual information imply dependency at the significance level
However, most of the argument — particularly, Lemma 1 and Theorem 1 — applies more generally. It in fact applies to algorithmic specified complexity, which, as we have seen, is defined quite similarly to algorithmic mutual information.
Let
and
be probability distributions over sequences (or any other kinds of objects from a countable domain) that correspond to the null and alternative hypotheses respectively; by
and
we denote the probabilities assigned to a sequence
by the respective distributions.
[…]
We now define the alternative hypothesis
in terms of encoding length. Let
denote a decoding algorithm [our universal prefix machine] that can reconstruct the target
[our
] based on its encoding relative to the source
[our context
]. By
[our
] we denote the length of the encoding [for us, this is the length of a shortest program that outputs
on input of
]. We make the standard assumption that encodings are prefix-free, i.e., that none of the encodings represented in binary is a prefix of another (for a detailed discussion of the prefix-free property, see Cover & Thomas, 1991; Li & Vitányi, 1993). We expect that the targets that are similar to the source will have short encodings. The following theorem states that a target
is unlikely to have an encoding much shorter than
THEOREM 1 For any distribution of probabilities
decoding algorithm
and source
Here is a specialization of Theorem 1 within the framework of this post: Let ![]() be a random variable with distribution
be a random variable with distribution ![]() of probability over the set
of probability over the set ![]() of binary strings. Let context
of binary strings. Let context ![]() be a binary string. Then the probability of algorithmic specified complexity
be a binary string. Then the probability of algorithmic specified complexity ![]() is at most
is at most ![]() i.e.,
i.e.,
![]()
For a simpler formulation and derivation, along with a snarky translation of the result into IDdish, see my post “Deobfuscating a Theorem of Ewert, Marks, and Dembski” at Bounded Science.
I emphasize that Milosavljević does not narrow his focus to algorithmic mutual information until Theorem 2. The reason that Theorem 1 applies to algorithmic specified complexity is not that ASC is essentially the same as algorithm mutual information — we established above that it is not — but instead that the theorem is quite general. Indeed, Theorem 1 does not apply directly to the algorithmic mutual information
![]()
because ![]() is a semimeasure, not a measure like
is a semimeasure, not a measure like ![]() Theorem 2 tacitly normalizes the probabilities of the semimeasure
Theorem 2 tacitly normalizes the probabilities of the semimeasure ![]() producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of
producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of ![]() stated in the abstract, which is different from the bound of
stated in the abstract, which is different from the bound of ![]() for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
Conclusion
In 2005, William Dembski made a radical change in what he called specified complexity, and developed the precursor of algorithmic specified complexity. He presented the “new and improved” specified complexity in terms of statistical hypothesis testing. That much of what he did made good sense. There are no formally established properties of algorithmic specified complexity that justify regarding it as a measure of meaningful information. The one theorem that Marks et al. have published is actually a special case of a 1995 result applied to hypothesis testing. In my own exploration of the properties of algorithmic specified complexity, I’ve seen nothing at all to suggest that it is reasonably regarded as a measure of meaning. Marks et al. have attached “meaning” rhetoric to some example applications of algorithmic specific complexity, but have said nothing about counterexamples, which are quite easy to find. In Evo-Info 5, I will explain how to use the methods of “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” to measure large quantities of “meaningful information” in nonsense images derived from the context.
The Series
Evo-Info review: Do not buy the book until…
Evo-Info 1: Engineering analysis construed as metaphysics
Evo-Info 2: Teaser for algorithmic specified complexity
Evo-Info sidebar: Conservation of performance in search
Evo-Info 3: Evolution is not search
Evo-Info 4: Non-conservation of algorithmic specified complexity
Evo-Info 4 addendum
[Some minor typographical errors in the original post have been corrected.]



Who or what creates information phoodoo? Presumably you think some sort of deity does it? When does that happen? How does that happen?
A tip of the hat to Dr. Seuss for trying to make sense of some of Alan’s confusion:
Dr. Seuss.
No, just a counter example to Corneel’s claim:
> Since natural selection depends on fitness variation, I don’t see how the target can possibly be independent from the evolutionary process.
Just because no evolutionary pathway exists from A to B does not imply that no pathway exists. I cannot turn a carriage into a car through Darwinian mechanisms, but I can through the incremental intelligent design of engineers.
Same with programming. I cannot progress from a simple hello world BASIC program to a 3D Java game through selection and random mutation, but I can through my own incremental learning and engineering.
And, we can justify this mathematically by the observation that a halting oracle O can create algorithmic mutual information, whereas randomness R and computation C cannot:
I(O(x):y) > I(x:y) >= E[I(C(R,x):y)]
EricMH,
Does your argument/proof work regardless of the how smooth or rugged the fitness landscape is?
If the fitness landscape is a smooth mountain with one peak, then my argument does not work. The more the landscape varies from this scenario the more my argument applies.
Does your math reflect this?
Also, another way to put it would be, the more the fitness landscape looks like islands of function, or hills that are far and between, the more your argument applies, right?
How does this work? I thought that Eric Holloway’s argument worked for all fitness surfaces. (But then I don’t understand how Holloway’s argument is connected to any fitness surfaces).
Joe Felsenstein,
Or to biological reality.
It does if we relabel them all to the same value!
This may seem frivolous, but it is a very rough idea of what population genetics claims can happen to genomes of populations over time.
I hope you mean you are trying to provide the detail needed to justify why your mathematical results have any application to biological evolution.
I think your overall argument follows this structure:
P1 E is a process which is consistent with known physics operating on Earth.
P2 M is a mathematical model of E.
P3 O are observations purportedly produced by E.
P4 M says O contradicts E.
Conclusion: E is false. That is, the process which produced O is not consistent with known physics operating on Earth.
For your argument as I understand it, E is the mechanism of natural selection operating under evolutionary theory, M is your AI model and Levin’s results, and O is the observed appearance of design in living organisms. Because of this conclusion, you say a halting oracle embodied by intelligence is required to produce O (of course, halting oracles are inconsistent with physics operating on Earth)..
But the real problem with this argument is premise 2. I see no reason to accept it over P1 in the case of your model applying to biological evolution, given the success of P1 throughout science. (It is of course MN, but this thread is not the place to discuss MN).
EricMH,
Eric:
I find it somewhat ironic that you have posted separately about the Wigner 1960 paper on the unreasonable effectiveness of math in physics.
Wigner’s examples, as well as his overall argument, start with scientists observing regularities and then seeking the mathematical equations which could model them. His examples involve Newton modeling observed motions on earth and in the solar system, and Born and others modeling observed results of experiments with quantum entities.
In both cases, science starts with unexplained empirical observations and then proceeds to find relevant math.
So far, your approach seems to be the opposite: start with math, then claim observations must fit it.
Hoarders keep things and that creates a mess.
QED
But isn’t evolution a process of constant relabeling?
Are you trying to supply the Creationists with yet more reasons to believe that evolutionary theory is not science?
A response a la Mung.
I’ve noticed this sort of response a lot, that somehow the physical world can contradict mathematics. It is Dr. Swamidass’ go to line over at PS whenever it seems the mathematics is correct. However, the physical world can never contradict mathematics. If our observations do not match our math, then the only possibility is a mistake has been made somewhere:
1. Flaw in measurement
2. Flaw in application of math
3. Flaw in mathematical proof
If 1-3 do not apply, then math and the physical world will line up perfectly.
I believe the disagreement between ID and the TSZ folks is deeper than the biology. The fundamental disagreement is TSZ believes the physical world can truly contradict mathematics.
Those of us who make mathematical models of the real world are painfully aware that reality can, and usually does, fail to match our models. I’m unaware of anyone who makes these models trying to explain away that discrepancy by asserting that they have contradicted mathematics itself.
Just to echo Joe Felsenstein here, Eric. Ask yourself, if a mathematical model doesn’t match reality, which is likely to be incorrect, reality or the math model?
Eric is saying that when a mathematical model conflicts with reality, that we here at TSZ then go around saying that reality contradicts, not that particular model, but the basic structures of mathematics itself.
Of course it would be silly to do that. Do you have an example of someone here doing that, Eric?
These latest comments from BruceS, Eric, Alan, and Joe are really getting to the heart of the matter.
No. I would in fact state that there is no logically possible world in which mathematics does not obtain. But mathematics does not have to be designed for that to be the case, rather it must necessarily be so. In so far as some world is logically coherent, then it must be possible to count, and relations of quantity must follow.
This is not something which God is required to explain, or create, or for which mathematics has to be designed, rather it cannot be otherwise. To say anything else is absolutely gibberish, nonsense, poppycock. It is literally inconceivable, and that really is the word I intend to employ.
I am sorry. Did I miss something? Where did the math contradict the physical world?
Didn’t Eric just say that he could mathematically prove that a population could not evolve to a higher fitness level, provided that no evolutionary pathway exists. That seems exactly right. Rather trivial, no?
Since Eric conceded that his argument does not apply to all fitness surfaces, doesn’t that mean it fails as a general proof that natural selection cannot increase specified complexity?
And can we work through the example, please? It has a simple fitness surface with a single peak, so I gues we should be able to establish why the proof fails in this particular scenario.
Eric: I notice you say “mathematics” and not “mathematical model”, as others responding to your post here are taking you to say.
If you did mean to refer to mathematical model, then your list fails to appreciate how and why scientists build models. First, most models deliberately omit features of reality through abstraction or idealization. Second, many scientific models are not mathematical since modes of explanation must be tailored to the explanatory needs of a scientific domain. See this article in SEP if you are interested in learning about scientific modeling and here for scientific explanation.
But suppose you meant “mathematics” per se. In this case, I take you to be asserting that the world has a fundamental structure which can be captured mathematically (that would include the Tegmarkian position that the world is mathematical). I happen to sympathize with the position that fundamentally the world can be described by mathematical structure, expresssed as the philosophical position of structural realism, but even if that controversial view is correct, we still have this key issue:
How do we limited, fallible humans discover the mathematical structure of the world?
As I have said in past posts, I see ID theorists as modern day rationalists: “rationalism is defined as a methodology or a theory “in which the criterion of the truth is not sensory but intellectual and deductive” (quoted in Wiki). Most ID theorists seem to believe that armchair theorizing using the mathematics of information and complexity combined with combinatorial probability are the correct ways to understanding the nature of reality; they reject modern scientifically-grounded empiricism.
This is the fundamental difference between science and ID theory.
Eric has a lot of work to do to make explicit how his mathematics says anything at all about biology, let alone fitness surfaces. Any comments on those topics he posts are his personal view of what his theory says. He has admitted in other posts he knows little of biology.
Until that work is done, working through any examples would be premature.
There are several threads at Peaceful Science where Eric explains his theory in more detail.
https://discourse.peacefulscience.org/u/ericmh/summary
A Unified Model of Complex Specified Information
H/T: Dan Eastwood at Peaceful Science.
I have not read, but from a quick look at examples provided in the paper, I see one: electronic coin flipper.
Thanks. I followed several of those but they fail to illuminate. “X is a biological organism” is not something I can work with; I need to know how to represent that organism in mathematical terms. I suspect working through the example will remain perpetually premature, but at least we get to find out what variables Eric thinks are appropriate to feed into the equations.
ETA: loved your comment about the failure to distinguish mathematics from mathematical models: spot on.
I think when Corneel says “the mathematical model”, what was meant was my simple population-genetic model of natural selection in an organism, the one in this 2012 post that I referred Eric to. The equations are simple, and they show that the model is, generation by generation, enriching the frequency of the highly-fit haploid genomes, by increasing the gene frequency of the advantageous allele at each locus. Further knowledge of the biology is not needed — I called the beasts “wombats” just for fun, but they could equally easily be jellyfish or warble flies or baobab trees.
I don’t see what stops EricMH from showing how his ASC argument applies to my model. Or showing how the simple fitness surface it has — one that is smooth and has a single peak, violates some condition in his argument. I don’t see any condition or assumption in his argument that says anything about the smoothness issue. But EricMH is much more familiar with his argument than I am, so if that condition is there, presumably he can show us where in the argument it is.
I disagree with BruceS that looking in EricMH’s argument for this is premature.
I can promise you that if we find out how EricMH’s model shows that fitness cannot increase in a simple population-genetic model like this, the effect of this on population genetics would be very large — some of the foundational papers on natural selection would have to be retracted, 94 years of work down the drain.
I agree and posted some time ago in your thread that Eric start there and then respond to your feedback and that of the other biologists. I understood that Corneel was asking for something much more specific than that as a starting point, but of course that could just reflect my own ignorance of biology.
ETA: With my limited knowledge in mind: my best understanding of Eric’s MI theory is that he is looking at (Kolmogorov) MI of a given genome to its mutated successor. (And evolved successor too perhaps, thought is unclear to me what that could mean)
But what he should be looking at, I think, is
the MI between the aggregate genome of a population and the environment
versus
the MI of the aggregate genome of successor populations and the environment after population genetics mechanisms have operated on the aggregated genome.
How exactly that aggregate genome/environment MI is modeled using Algorithmic Complexity is a problem I leave for Eric!
Haha, all the talk of fitness surfaces threw you off, I’ll bet. I was indeed referring to Joe’s “haploid wombat” example. It too has a fitness surface associated with it, which can be easily represented for any single locus by plotting the allele frequency at the x-axis and the average population fitness on the y-axis. I believe it is a simple straight line going up with increasing frequency of the “1”-allele.
Plotting multi-locus genotypes will be messy, but the fitness landscape is straightforward and gently sloping up, with a single peak at the population that is fixed for “1” at all loci.
ETA: fixed mistake
If the gene frequency at a locus is , the mean fitness at that locus is
, the mean fitness at that locus is  in the numerical example, which is indeed linear. For 100 loci the mean fitnesses at the 100 loci can be multiplied to get the overall mean fitness. In my example the gene frequencies at the 100 loci are all the same,
in the numerical example, which is indeed linear. For 100 loci the mean fitnesses at the 100 loci can be multiplied to get the overall mean fitness. In my example the gene frequencies at the 100 loci are all the same,  , so that the mean fitness of the population is then
, so that the mean fitness of the population is then  , which rises in an exponential curve from 1.6566 when
, which rises in an exponential curve from 1.6566 when  to 2.7048 when
to 2.7048 when  .
.
Ah, if all loci have the same frequency for the “1” allele, then we can actually make a nice visualization of the fitness landscape.
According to Alan organisms do not adapt. Is it then only parts of organisms that adapt? Organisms do not adapt but alleles do adapt?
Well, my education (if not vocation) was in math, so I’m OK with the math bit. It’s how much biological basic work needs to be in place to even talk about fitness surfaces that I wondered about.
I think Eric needs to start with explaining some very basic aspects of how his theory is meant to model biology. Like what strings his mutual information is supposed to be between. Or how relative fitness is captured. Or how mechanisms like NS are captured.
I understand he thinks his theory can rule out naturalistic explanations of NS, but first I think he needs to explain how all of these concepts are even represented in models based on his theory.
Based on his latest post, the issue may be that Eric does agree with the scientific approach to modeling.
Wouldn’t the proper comparison be between ID and the armchair theorizing of evolutionary biology?
F=ma. Except when it doesn’t.
Its all in the niche.
No. Because such theorizing is only part of science, not its whole, and conforms to norms of scientific modeling if it is to be accepted by scientific community (ETA as something more than a useful teaching tool or as a part of a popularization).
For an interesting discussion that involves this point among others, see Daniel Ang’s posts about Dark Matter and about Math and Physics at PS.
Eric tried to make the same point about thought experiments by eg Einstein at one point, and he was wrong for the same reason.
Wait, this was a Mung post ETA 2: But if your post was not meant to be taken seriously, then never mind.
Unless his goal is to join de DI and sell books to creationists
Good plot, but would be more informative if you had the argument ylim=c(0,3) in your R plot command so as not to give the impression that mean fitness is zero at the left end of the plot.
OK, I said “in an organism” when I should have said, more clearly, “in a population”.
Individual organisms can change adaptively (or maladaptively). That is an interesting topic for someone else to discuss somewhere else.
Sure, and I appreciated the opportunity to demystify fitness landscapes. Nothing fancy needed as you can see; you could make one for any model where genotypes / phenotypes need to be mapped to fitness.
100% agree
The issue may be that he is stalllllling 😉
Agreed, and I think that a line looks nicer too. Here comes take two:
I don’t think that this is fair, even in jest. Everyone should have time to think about what they have to say, especially when addressing such a fundamental issue.
It’s kindergarten stuff learning that the math models the reality, but it’s not the same as the reality. Eric might have missed kindergarten.
I understand you are not serious.
So in that spirit, let me point out (before Mung does!). That same concern has been expressed about string theory and the new physicists who concentrate on it rather than looking for new ideas in unifying GR/QFT. Namely, string theory is the main game in town for such physicists, and so they have to study it and support it to build a career by publishing papers and to earn a living as a postdoc.
But this is not to question their sincerity in believing in string theory as a valid approach to the issue. Similarly, from all I know of Eric here and at PS, I believe he is sincere in his belief that ID theory is a valid approach to understanding the appearance of design in nature.
Corneel
Again, I understand you are being humorous (despite me being on the spectrum with respect to to reading the emotional import of emojis). But I do want to emphasize that based on all the posts I have seen from Eric here and at PS, I think he is sincere and honest about his beliefs.
Mathematics are used to try and represent observations. It’s the observations that rule the math, not the other way around. So, if this is The Disagreement, then it is one where ID would be making a fundamental cart-before-the-horse philosophical blunder. It’s obvious that the math is used to make representations of phenomena, not phenomena to make representations of the math.
To be fair, some actual scientists talk, or even write whole books, making the very same cart-before-the-horse blunders. For example, in some interview, Kraus, or some other physicist, talked about “the equations that govern the universe.” I thought, what an idiot, and stopped reading right there.
We seem to be failing at teaching philosophy properly after kindergarten, and most people forget kindergarten, so we’re left with this mess.
I don’t think the abuse is appropriate. I would like to hear more about what Eric thinks about the relationship between modeling and the ID movement.
Edit: Because I think he is articulating a faulty point of view that underlies the work of Dembski and Marks.
You are correct with regards to mathematics.
But there is a real issue with the nature of the laws of physics. Namely, are they necessary: do they always apply? If so, how can necessity be a feature of the world? If not, why is physics so successful in explaining and predicting regularities?
One can try arguing that such regularities are simply things we humans impose on reality, but that view has issues as well.
https://plato.stanford.edu/entries/laws-of-nature/
Philosophy for sure, though maybe a bit advanced for kindergarten.
Stephen Hawking:
[start of quote]
Even if there is only one possible unified theory, it is just a set of rules and equations. What is it that breathes fire into the equations and makes a universe for them to describe?
(A Brief History of Time, p. 190)