Subjects: Evolutionary computation. Information technology–Mathematics.
The greatest story ever told by activists in the intelligent design (ID) socio-political movement was that William Dembski had proved the Law of Conservation of Information, where the information was of a kind called specified complexity. The fact of the matter is that Dembski did not supply a proof, but instead sketched an ostensible proof, in No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002). He did not go on to publish the proof elsewhere, and the reason is obvious in hindsight: he never had a proof. In “Specification: The Pattern that Signifies Intelligence” (2005), Dembski instead radically altered his definition of specified complexity, and said nothing about conservation. In “Life’s Conservation Law: Why Darwinian Evolution Cannot Create Biological Information” (2010; preprint 2008), Dembski and Marks attached the term Law of Conservation of Information to claims about a newly defined quantity, active information, and gave no indication that Dembski had used the term previously. In Introduction to Evolutionary Informatics, Marks, Dembski, and Ewert address specified complexity only in an isolated chapter, “Measuring Meaning: Algorithmic Specified Complexity,” and do not claim that it is conserved. From the vantage of 2018, it is plain to see that Dembski erred in his claims about conservation of specified complexity, and later neglected to explain that he had abandoned them.
Algorithmic specified complexity is a special form of specified complexity as Dembski defined it in 2005, not as he defined it in earlier years. Yet Marks et al. have cited only Dembski’s earlier publications. They perhaps do not care to draw attention to the fact that Dembski developed his “new and improved” specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. That’s obviously quite different from their current presentation of algorithmic specified complexity as a measure of meaning. Ironically, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then [sic] or equal to
bits of ASC is less then [sic] or equal to ![]() ” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing, Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995). It is odd that Marks et al. have not discovered this result in a literature search, given that they have emphasized the formal similarity of algorithmic specified complexity to algorithmic mutual information.
Lately, a third-wave ID proponent by the name of Eric Holloway has spewed mathematicalistic nonsense about the relationship of specified complexity to algorithmic mutual information. [Note: Eric has since joined us in The Skeptical Zone, and I sincerely hope to see that he responds to challenges by making better sense than he has previously.] In particular, he has claimed that a conservation law for the latter applies to the former. Given his confidence in himself, and the arcaneness of the subject matter, most people will find it hard to rule out the possibility that he has found a conservation law for specified complexity. My response, recorded in the next section of this post, is to do some mathematical investigation of how algorithmic specified complexity relates to algorithmic mutual information. It turns out that a demonstration of non-conservation serves also as an illustration of the senselessness of regarding algorithmic specified complexity as a measure of meaning.
Let’s begin by relating some of the main ideas to pictures. The most basic notion of nongrowth of algorithmic information is that if you input data ![]() to computer program
to computer program ![]() then the amount of algorithmic information in the output data
then the amount of algorithmic information in the output data ![]() is no greater than the amounts of algorithmic information in input data
is no greater than the amounts of algorithmic information in input data ![]() and program
and program ![]() added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image
added together. That is, the increase of algorithmic information in data processing is limited by the amount of algorithmic information in the processor itself. The following images do not illustrate the sort of conservation just described, but instead show massive increase of algorithmic specified complexity in the processing of a digital image ![]() by a program
by a program ![]() that is very low in algorithmic information. At left is the input
that is very low in algorithmic information. At left is the input ![]() and at right is the output
and at right is the output ![]() of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the
of the program, which cumulatively sums of the RGB values in the input. Loosely speaking, the ![]() -th RGB value of Signature of the Id is the sum of the first
-th RGB value of Signature of the Id is the sum of the first ![]() RGB values of Fuji Affects the Weather.
RGB values of Fuji Affects the Weather.
What is most remarkable about the increase in “meaning,” i.e., algorithmic specified complexity, is that there actually is loss of information in the data processing. The loss is easy to recognize if you understand that RGB values are 8-bit quantities, and that the sum of two of them is generally a 9-bit quantity, e.g.,
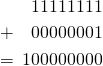
The program ![]() discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image
discards the leftmost carry (either 1, as above, or 0) in each addition that it performs, and thus produces a valid RGB value. The discarding of bits is loss of information in the clearest of operational terms: to reconstruct the input image ![]() from the output image
from the output image ![]() you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
you would have to know the bits that were discarded. Yet the cumulative summation of RGB values produces an 11-megabit increase in algorithmic specified complexity. In short, I have provided a case in which methodical corruption of data produces a huge gain in what Marks et al. regard as meaningful information.
An important detail, which I cannot suppress any longer, is that the algorithmic specified complexity is calculated with respect to binary data called the context. In the calculations above, I have taken the context to be the digital image Fuji. That is, a copy of Fuji has 13 megabits of algorithmic specified complexity in the context of Fuji, and an algorithmically simple corruption of Fuji has 24 megabits of algorithmic specified complexity in the context of Fuji. As in Evo-Info 2, I have used the methods of Ewert, Dembski, and Marks, “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” (2015). My work is recorded in a computational notebook that I will share with you in Evo-Info 5. In the meantime, any programmer who knows how to use an image-processing library can easily replicate my results. (Steps: Convert fuji.png to RGB format; save the cumulative sum of the RGB values, taken in row-major order, as signature.png; then subtract 0.5 Mb from the sizes of fuji.png and signature.png.)
As for the definition of algorithmic specified complexity, it is easiest to understand when expressed as a log-ratio of probabilities,
![]()
where ![]() and
and ![]() are binary strings (finite sequences of 0s and 1s), and
are binary strings (finite sequences of 0s and 1s), and ![]() and
and ![]() are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above,
are distributions of probability over the set of all binary strings. All of the formal details are given in the next section. Speaking loosely, and in terms of the example above, ![]() is the probability that a randomly selected computer program converts the context
is the probability that a randomly selected computer program converts the context ![]() into the image
into the image ![]() and
and ![]() is the probability that image
is the probability that image ![]() is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of
is the outcome of a default image-generating process. The ratio of probabilities is the relative likelihood of ![]() arising by an algorithmic process that depends on the context, and of
arising by an algorithmic process that depends on the context, and of ![]() arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that
arising by a process that does not depend on the context. If, proceeding as in statistical hypothesis testing, we take as the null hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() and as an alternative hypothesis the proposition that
and as an alternative hypothesis the proposition that ![]() is the outcome of a process with distribution
is the outcome of a process with distribution ![]() then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of
then our level of confidence in rejecting the null hypothesis in favor of the alternative hypothesis depends on the value of ![]() The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level
The one and only theorem that Marks et al. have given for algorithmic specified complexity tells us to reject the null hypothesis in favor of the alternative hypothesis at confidence level ![]() when
when ![]()
What we should make of the high algorithmic specified complexity of the images above is that they both are more likely to derive from the context than to arise in the default image-generating process. Again, Fuji is just a copy of the context, and Signature is an algorithmically simple corruption of the context. The probability of randomly selecting a program that cumulatively sums the RGB values of the context is much greater than the probability of generating the image Signature directly, i.e., without use of the context. So we confidently reject the null hypothesis that Signature arose directly in favor of the alternative hypothesis that Signature derives from the context.
This embarrassment of Marks et al. is ultimately their own doing, not mine. It is they who buried the true story of Dembski’s (2005) redevelopment of specified complexity in terms of statistical hypothesis testing, and replaced it with a fanciful account of specified complexity as a measure of meaningful information. It is they who neglected to report that their theorem has nothing to do with meaning, and everything to do with hypothesis testing. It is they who sought out examples to support, rather than to refute, their claims about meaningful information.
Algorithmic specified complexity versus algorithmic mutual information
This section assumes familiarity with the basics of algorithmic information theory.
Objective. Reduce the difference in the expressions of algorithmic specified complexity and algorithmic mutual information, and provide some insight into the relation of the former, which is unfamiliar, to the latter, which is well understood.
Here are the definitions of algorithmic specified complexity (ASC) and algorithmic mutual information (AMI):
![]()
where ![]() is a distribution of probability over the set
is a distribution of probability over the set ![]() of binary strings,
of binary strings, ![]() and
and ![]() are binary strings, and binary string
are binary strings, and binary string ![]() is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity
is a shortest program, for the universal prefix machine in terms of which the algorithmic complexity ![]() and the conditional algorithmic complexity
and the conditional algorithmic complexity ![]() are defined, outputting
are defined, outputting ![]() The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of
The base of the logarithm is 2. Marks et al. regard algorithmic specified complexity as a measure of the meaningful information of ![]() in the context of
in the context of ![]()
The law of conservation (nongrowth) of algorithmic mutual information is:
![]()
for all binary strings ![]() and
and ![]() and for all computable [ETA 12/12/2019: total] functions
and for all computable [ETA 12/12/2019: total] functions ![]() on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability
on the binary strings. The analogous relation for algorithmic specified complexity does not hold. For example, let the probability ![]() where
where ![]() is the empty string, and let
is the empty string, and let ![]() be positive for all nonempty binary strings
be positive for all nonempty binary strings ![]() Also let
Also let ![]() for all binary strings
for all binary strings ![]() Then for all nonempty binary strings
Then for all nonempty binary strings ![]() and for all binary strings
and for all binary strings ![]()
![]()
because
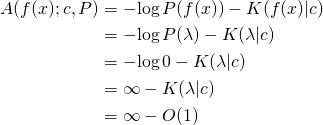
is infinite and ![]() is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that
is finite. [Edit: The one bit of algorithmic information theory you need to know, in order to check the proof, is that ![]() is finite for all binary strings
is finite for all binary strings ![]() and
and ![]() I have added a line at the end of the equation to indicate that
I have added a line at the end of the equation to indicate that ![]() is not only finite, but also constant.] Note that this argument can be modified by setting
is not only finite, but also constant.] Note that this argument can be modified by setting ![]() to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing
to an arbitrarily small positive number instead of to zero. Then the growth of ASC due to data processing ![]() can be made arbitrarily large, though not infinite.
can be made arbitrarily large, though not infinite.
There’s a simple way to deal with the different subexpressions ![]() and
and ![]() in the definitions of ASC and AMI, and that is to restrict our attention to the case of
in the definitions of ASC and AMI, and that is to restrict our attention to the case of ![]() in which the context is a shortest program outputting
in which the context is a shortest program outputting ![]()
![]()
This is not an onerous restriction, because there is for every string ![]() a shortest program
a shortest program ![]() that outputs
that outputs ![]() In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as
In fact, there would be no practical difference for Marks et al. if they were to require that the context be given as ![]() We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
We might have gone a different way, replacing the contemporary definition of algorithmic mutual information with an older one,
![]()
However, the older definition comes with some disadvantages, and I don’t see a significant advantage in using it. Perhaps you will see something that I have not.
The difference in algorithmic mutual information and algorithmic specified complexity,
![]()
has no lower bound, because ![]() is non-negative for all
is non-negative for all ![]() and
and ![]() is negatively infinite for all
is negatively infinite for all ![]() such that
such that ![]() is zero. It is helpful, in the following, to keep in mind the possibility that
is zero. It is helpful, in the following, to keep in mind the possibility that ![]() for a string
for a string ![]() with very high algorithmic complexity, and that
with very high algorithmic complexity, and that ![]() for all strings
for all strings ![]() Then the absolute difference in
Then the absolute difference in ![]() and
and ![]() [added 11/11/2019: the latter expression should be
[added 11/11/2019: the latter expression should be ![]() ] is infinite for all
] is infinite for all ![]() and very large, though finite, for
and very large, though finite, for ![]() There is no limit on the difference for
There is no limit on the difference for ![]() Were Marks et al. to add a requirement that
Were Marks et al. to add a requirement that ![]() be positive for all
be positive for all ![]() we still would be able, with an appropriate definition of
we still would be able, with an appropriate definition of ![]() to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all
to make the absolute difference of AMI and ASC arbitrarily large, though finite, for all ![]()
The remaining difference in the expressions of ASC and AMI is in the terms ![]() and
and ![]() The easy way to reduce the difference is to convert the algorithmic complexity
The easy way to reduce the difference is to convert the algorithmic complexity ![]() into an expression of log-improbability,
into an expression of log-improbability, ![]() where
where
![]()
for all binary strings ![]() An elementary result of algorithmic information theory is that the probability function
An elementary result of algorithmic information theory is that the probability function ![]() satisfies the definition of a semimeasure, meaning that
satisfies the definition of a semimeasure, meaning that ![]() In fact,
In fact, ![]() is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
is called the universal semimeasure. A semimeasure with probabilities summing to unity is called a measure. We need to be clear, when writing
![]()
that ![]() is a measure, and that
is a measure, and that ![]() is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made
is a semimeasure, not a measure. (However, in at least one of the applications of algorithmic specified complexity, Marks et al. have made ![]() a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
a semimeasure, not a measure.) This brings us to a simple characterization of ASC:
This does nothing but to establish clearly a sense in which algorithmic specified complexity is formally similar to algorithmic mutual information. As explained above, there can be arbitrarily large differences in the two quantities. However, if we consider averages of the quantities over all strings ![]() holding
holding ![]() constant, then we obtain an interesting result. Let random variable
constant, then we obtain an interesting result. Let random variable ![]() take values in
take values in ![]() with probability distribution
with probability distribution ![]() Then the expected difference of AMI and ASC is
Then the expected difference of AMI and ASC is
![Rendered by QuickLaTeX.com \begin{align*} E[I(X : c) - A(X; c^*\!, P)] &= E[K(X) + \log P(X)] \\ &= E[K(X)] - E[-\!\log P(X)] \\ &= E[K(X)] - H(P). \end{align*}](http://theskepticalzone.com/wp/wp-content/ql-cache/quicklatex.com-318f3c5b560e1b1e12090c6f7bfdfa71_l3.png)
Introducing a requirement that function ![]() be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
be computable, we get lower and upper bounds on the expected difference from Theorem 10 of Grünwald and Vitányi, “Algorithmic Information Theory“:
![]()
Note that the algorithmic complexity of computable probability distribution ![]() is the length of the shortest program that, on input of binary string
is the length of the shortest program that, on input of binary string ![]() and number
and number ![]() (i.e., a binary string interpreted as a non-negative integer), outputs
(i.e., a binary string interpreted as a non-negative integer), outputs ![]() with
with ![]() bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
bits of precision (see Example 7 of Grünwald and Vitányi, “Algorithmic Information Theory“).
![]()
How much the expected value of the AMI may exceed the expected value of the ASC depends on the length of the shortest program for computing ![]()
[Edit 10/30/2019: In the preceding box, there were three instances of ![]() that should have been
that should have been ![]() ] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If
] Next we derive a similar result, but for individual strings instead of expectations, applying a fundamental result in algorithmic information theory, the MDL bound. If ![]() is computable, then for all binary strings
is computable, then for all binary strings ![]() and
and ![]()
(MDL) 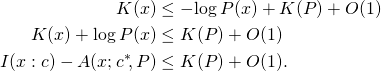
Replacing string ![]() in this inequality with a string-valued random variable
in this inequality with a string-valued random variable ![]() as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
as we did previously, and taking the expected value, we obtain one of the inequalities in the box above. (The cross check increases my confidence, but does not guarantee, that I’ve gotten the derivations right.)
Finally, we express ![]() in terms of the universal conditional semimeasure,
in terms of the universal conditional semimeasure,
![]()
Now ![]() and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that
and we can express algorithmic specified complexity as a log-ratio of probabilities, with the caveat that ![]()
![]()
where ![]() is a distribution of probability over the binary strings
is a distribution of probability over the binary strings ![]() and
and ![]() is the universal conditional semimeasure.
is the universal conditional semimeasure.
An old proof that high ASC is rare
Marks et al. have fostered a great deal of confusion, citing Dembski’s earlier writings containing the term specified complexity — most notably, No Free Lunch: Why Specified Complexity Cannot Be Purchased without Intelligence (2002) — as though algorithmic specified complexity originated in them. The fact of the matter is that Dembski radically changed his approach, but not the term specified complexity, in “Specification: The Pattern that Signifies Intelligence” (2005). Algorithmic specified complexity derives from the 2005 paper, not Dembski’s earlier work. As it happens, the paper has received quite a bit of attention in The Skeptical Zone. See, especially, Elizabeth Liddle’s “The eleP(T|H)ant in the room” (2013).
Marks et al. furthermore have neglected to mention that Dembski developed the 2005 precursor (more general form) of algorithmic specified complexity as a test statistic, for use in rejecting a null hypothesis of natural causation in favor of an alternative hypothesis of intelligent, nonnatural intervention in nature. Amusingly, their one and only theorem for algorithmic specified complexity, “The probability of obtaining an object exhibiting ![]() bits of ASC is less then or equal to
bits of ASC is less then or equal to ![]() ” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
” is a special case of a more general result for hypothesis testing. The result is Theorem 1 in A. Milosavljević’s “Discovering Dependencies via Algorithmic Mutual Information: A Case Study in DNA Sequence Comparisons” (1995), which Marks et al. do not cite, though they have pointed out that algorithmic specified complexity is formally similar to algorithmic mutual information.
According to the abstract of Milosavljević’s article:
We explore applicability of algorithmic mutual information as a tool for discovering dependencies in biology. In order to determine significance of discovered dependencies, we extend the newly proposed algorithmic significance method. The main theorem of the extended method states that
bits of algorithmic mutual information imply dependency at the significance level
However, most of the argument — particularly, Lemma 1 and Theorem 1 — applies more generally. It in fact applies to algorithmic specified complexity, which, as we have seen, is defined quite similarly to algorithmic mutual information.
Let
and
be probability distributions over sequences (or any other kinds of objects from a countable domain) that correspond to the null and alternative hypotheses respectively; by
and
we denote the probabilities assigned to a sequence
by the respective distributions.
[…]
We now define the alternative hypothesis
in terms of encoding length. Let
denote a decoding algorithm [our universal prefix machine] that can reconstruct the target
[our
] based on its encoding relative to the source
[our context
]. By
[our
] we denote the length of the encoding [for us, this is the length of a shortest program that outputs
on input of
]. We make the standard assumption that encodings are prefix-free, i.e., that none of the encodings represented in binary is a prefix of another (for a detailed discussion of the prefix-free property, see Cover & Thomas, 1991; Li & Vitányi, 1993). We expect that the targets that are similar to the source will have short encodings. The following theorem states that a target
is unlikely to have an encoding much shorter than
THEOREM 1 For any distribution of probabilities
decoding algorithm
and source
Here is a specialization of Theorem 1 within the framework of this post: Let ![]() be a random variable with distribution
be a random variable with distribution ![]() of probability over the set
of probability over the set ![]() of binary strings. Let context
of binary strings. Let context ![]() be a binary string. Then the probability of algorithmic specified complexity
be a binary string. Then the probability of algorithmic specified complexity ![]() is at most
is at most ![]() i.e.,
i.e.,
![]()
For a simpler formulation and derivation, along with a snarky translation of the result into IDdish, see my post “Deobfuscating a Theorem of Ewert, Marks, and Dembski” at Bounded Science.
I emphasize that Milosavljević does not narrow his focus to algorithmic mutual information until Theorem 2. The reason that Theorem 1 applies to algorithmic specified complexity is not that ASC is essentially the same as algorithm mutual information — we established above that it is not — but instead that the theorem is quite general. Indeed, Theorem 1 does not apply directly to the algorithmic mutual information
![]()
because ![]() is a semimeasure, not a measure like
is a semimeasure, not a measure like ![]() Theorem 2 tacitly normalizes the probabilities of the semimeasure
Theorem 2 tacitly normalizes the probabilities of the semimeasure ![]() producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of
producing probabilities that sum to unity, before applying Theorem 1. It is this special handling of algorithmic mutual information that leads to the probability bound of ![]() stated in the abstract, which is different from the bound of
stated in the abstract, which is different from the bound of ![]() for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
for algorithmic specified complexity. Thus we have another clear indication that algorithmic specified complexity is not essentially the same as algorithmic mutual information, though the two are formally similar in definition.
Conclusion
In 2005, William Dembski made a radical change in what he called specified complexity, and developed the precursor of algorithmic specified complexity. He presented the “new and improved” specified complexity in terms of statistical hypothesis testing. That much of what he did made good sense. There are no formally established properties of algorithmic specified complexity that justify regarding it as a measure of meaningful information. The one theorem that Marks et al. have published is actually a special case of a 1995 result applied to hypothesis testing. In my own exploration of the properties of algorithmic specified complexity, I’ve seen nothing at all to suggest that it is reasonably regarded as a measure of meaning. Marks et al. have attached “meaning” rhetoric to some example applications of algorithmic specific complexity, but have said nothing about counterexamples, which are quite easy to find. In Evo-Info 5, I will explain how to use the methods of “Measuring Meaningful Information in Images: Algorithmic Specified Complexity” to measure large quantities of “meaningful information” in nonsense images derived from the context.
The Series
Evo-Info review: Do not buy the book until…
Evo-Info 1: Engineering analysis construed as metaphysics
Evo-Info 2: Teaser for algorithmic specified complexity
Evo-Info sidebar: Conservation of performance in search
Evo-Info 3: Evolution is not search
Evo-Info 4: Non-conservation of algorithmic specified complexity
Evo-Info 4 addendum
[Some minor typographical errors in the original post have been corrected.]



Everyone here knows I’m not qualified to make pronouncements in either physics or philosophy, but my years as a spectator lead me to agree with those who hold that “laws” of nature are approximations that require continuous updates and refinement. Alas, they are more like guidelines than laws.
Really good ones, but not binding on future observations.
As for math ruling out evolution, one should not bet against the results of races that have already been run.
No issue. The laws of physics are models of some phenomena studied by physicists.
Nope. They’re not necessary. The phenomena continue going on, no matter if we make models about them or not.
I think you are mistaking the phenomena for their representations. The phenomena might be consistent and be well represented by some equations within some range of observations, then be consistent in a different way at other ranges, or less consistent at another range, and so on and so forth. Physics is successful at predicting regularities when the observations don’t fall beyond the usability of the equations. But, haven’t you heard the phrase “this is where the laws of physics break”? I suspect it to mean “this is as far as our models might be able to help us understand, beyond that we’re clueless.”
It depends.
Boyle’s law is false, so cannot be necessary. It is, however, a good approximation.
Newton’s laws of motion are analytic, so necessary truths. And thus they always apply.
Ohm’s law is a bit of a mixture. It depends on how you look at it. In one way of looking at it, Ohm’s law is a useful approximation, but not strictly true and thus not a necessary truth. That’s probably how power engineers should look at it. The other way of looking at it is to take Ohm’s law to be a definition of resistance, and thus a necessary truth. That’s about the way it should be seen by electronics engineers.
The necessity of some of the laws of physics comes from their logical structure, which is due to the way that those laws were constructed by human scientists. Strictly speaking, it is the humans rather than the laws of physics that are features of the world.
Freelurker and BruceS,
Seems like I have triggered a similar response in both of you.
My comment was partly in jest, but I admit that I am getting a little impatient to see the demonstration of this imminent revolution in evolutionary biology. Given the far reaching implications of the claim, if correct, we have seen preciously little yet of even the most basic requirements, such as how to calculate ASC of a biological entity. Also, I confess that I am not entirely convinced yet that clarification of Eric’s proof will be forthcoming … ever.
Maybe I am being overly suspicious here, but we’ll see.
It would help if you could express your suspicions in a less accusatory tone.
point taken.
As strange as it may seem, there are many things that lay claim to my free time, and clarifying my argument is not the highest priority. But, it is on my list and I intend to get to it. Just might be quite awhile. I have concrete ideas in mind, but the concern is that just throwing them out before careful thought and dotting all ‘i’s and crossing all ‘t’s won’t result in productive discussion.
You all understand don’t you that the “laws of evolutionary biology” are not like the “laws of physics” and that evolutionary biology is still not considered to be among the “hard” sciences. So please stop pretending like they are in the same category.
Thank you
That’s good to hear and I am looking forward to it. Let me just mention that getting my hands dirty is what helps me most in gaining understanding of a new topic, which is why I am rather anxious to see some applications of the theory.
I have not claimed this. As you didn’t link, I can’t be sure if something I did claim was unclear. Perhaps you could indicate where you managed to infer that from something I wrote.
Nor sure why you brought this up. I don’t see any references to biological evolution as a law of nature the the thread. Did I miss it? The law stuff I brought up was in response to Entropy’s Kraus quote about equations of the universe, which I think referred to physics.
I am pretty sure I have only characterized evolution as a successful scientific model Of course, the relation between models and theories is philosophically vexed (surprise, surprise)..
In any event, your point about laws in special sciences is not as straightforward as you seem to believe. See
https://plato.stanford.edu/entries/ceteris-paribus/
Also Cartwright raises issues about the laws of nature expressed by physics at the link I provided to Entropy on laws..
You are welcome.
I agree that models are separate from laws and that representations are separate from the world they represent.
The issue I was trying to raise was different.
In fact, there are two issues, and I did not separate them well (mainly because I forgot about the separation when I wrote the response).
First there is the issue of metaphysical necessity: true in all possible worlds. The philosophical case for that is presented in the SEP article I linked. FWIW, I don’t think that the metaphysical necessity of laws holds.
There is also nomological necessity, which is best described in this IEP article:
I am not saying this view is true, only that is it philosophically respectable and may have been what Kraus and Hawking had in mind.
I don’t disagree with anything you way as being a respectable philosophical position. And I am not surprised it is what you believe.
My point, as I said in reply to Entropy, was that there are other respectable philosophical positions.
ETA: I mean respected by other philosophers, of course. Not necessarily by you!
I’m guessing you are referring to this comment where I wrote:
Now, I’m quite willing to expand on this but I’d like to know there would be some point, such as that my guess is correct and you would be interested in a more detailed reply.
This is still the way forward. When he has the time, Eric should deal with a model of reality (as he already indicated that he might.)
Nobody is talking about laws of evolutionary biology here.
The only thing I can imagine you to be arguing about here is my point, which stands, that our mathematical models try and describe phenomena, being thus dependent on our observations, and not the other way around. It’s ridiculous to suppose that phenomena now have to obey our models. So, Eric’s idea that the math modelling some phenomena cannot be “violated” by the phenomena is ass-backwards, and that doesn’t change whether it was something as precise as a “law” of physics, or something held to more complicated patterns, because of the many phenomena involved, like evolutionary biology.
You’re welcome, though I don’t know if that helped, I hope it did.
He should. I’d be happy if he doesn’t “deal with a model of reality” but just takes the simple mathematical model which has gene frequencies, and genotype frequencies, changing through time, and show how his argument applies there.
Only if by “philosophically respectable” you mean “respected by philosophers,” which doesn’t amount to much in my book. Philosophers find a lot of bullshit, and bullshitters, respectable.
Hawking’s quote seems to distinguish the models/equations from the phenomena, and to be asking about something, some “property,” of the phenomena / universe / whatever that makes the modelling possible.
Dr. Felsenstein, I’ve put together a basic application which is sitting in review.
@EricMH: Thanks, will look forward to it.