Jonathan Bartlett, known here as JohnnyB, has written a very thought-provoking post titled, A New View of Irreducible Complexity. I was going to respond in a comment on his post, but I soon realized that I would be able to express my thoughts much more clearly if I composed a post of my own, discussing the points which he raises.
Before I continue, I would like to say that while I find JohnnyB’s argument problematic on several counts, I greatly appreciate the intellectual effort that went into the making of his slide presentation. I would also like to commend JohnnyB on his mathematical rigor, which has helped illuminate the key issues.
Without further ado, I’d like to focus on some of the key slides in JohnnyB’s talk (shown in blue), and offer my comments on each of them. By the time I’m done, readers will be able to form their own assessment of the merits of JohnnyB’s argument.
Part One: What is JohnnyB trying to show?
Goals
Create a definition of Irreducible Complexity which shows that Darwinism is logically impossible over a wide range of assumptions.
Show the conditions for which evolution may or may not be possible…
[snip]
My Comments:
1. JohnnyB has set the bar very high here. He aims to show that a Darwinistic explanation of Irreducible Complexity is not merely vanishingly improbable, but logically impossible, like the term “married bachelor.” If he can do that, I’ll be very impressed. Not even Michael Behe claimed to be able to demonstrate this.
2. Right at the outset, JohnnyB assumes that the only good naturalistic explanation of Irreducible Complexity is a Darwinian one. That is Professor Richard Dawkins’ view, as JohnnyB points out later on in his talk. However, not all biologists agree with Dawkins.
Professor Larry Moran is a biochemist and a long-standing advocate of random genetic drift as the dominant mechanism of evolution. In a post titled, Constructive Neutral Evolution (CNE) (September 6, 2015), Moran goes further. Drawing on the work of Arlin Soltzfus, Michael Gray, Ford Doolittle, Michael Lynch, and Julius Lukes et al., Moran argues that non-adaptive mechanisms can account for the evolution of irreducibly complex systems. He illustrates his point with a simple hypothetical scenario (see here for a diagram):
Imagine an enzyme “A” that catalyzes a biochemical reaction as a single polypeptide chain. This enzyme binds protein “B” by accident in one particular species. That is, there is an interaction between A and B through fortuitous mutations on the surface of the two proteins. (Such interactions are common as confirmed by protein interaction databases.) The new heterodimer (two different subunits) doesn’t affect the activity of enzyme A. Since this interaction is neutral with respect to survival and reproduction, it could spread through the population by chance.
Over time, enzyme A might acquire additional mutations such that if the subunits were now separated the enzyme would no longer function (red dots). These mutations would be deleterious if there was no A + B complex but in the presence of such a complex the mutations are neutral and they could spread in the population by random genetic drift. Now protein B is necessary to suppress these new mutations making the heterodimer (A + B) irreducibly complex. Note that there was no selection for complexity — it happened by chance.
Further mutations might make the interaction more essential and make the two subunits more dependent on one another. This is a perfectly reasonable scenario for the evolution of irreducible complexity. Anyone who claims that the very existence of irreducibly complexity means that a structure could not have evolved is wrong. (Emphases mine – VJT.)
Throughout his talk, JohnnyB assumes that the evolution of irreducibly complex systems by chance processes is fantastically improbable. Perhaps this assumption is false. If it is, then his proof of the impossibility of irreducibly complex systems arising via unguided processes fails.
************************************************************************************************
Part Two: Evolution and computation

A Universal Turing machine U. U consists of a set of instructions in the table that can “execute” the correctly-formulated “code number” of any arbitrary Turing machine 
The following three slides from JohnnyB’s talk explain how he links Darwinian evolution to computation theory.
Why Computability Theory?
Evolution is, at its core, a statement about mapping changes in genotypes to changes in phenotypes.
In other words, there is a code which performs a function, and the change in code produces a change in function.
The mathematics developed to understand the relationship between codes and functions at a fundamental level is computability theory.
—————————————————————————————–
Turing’s Theory of Computation
All known paradigms of computation are reducible to Turing machines.
[snip]
—————————————————————————————–
Universal vs. Special Machines
A Turing machine is said to be a Universal machine if it can compute any computable function just by changing its tape.
Every Universal machine is equally powerful.
A non-universal Machine will only be able to implement a subset of computable functions.
If the set of needed functions is not known ahead of time, one must use a Universal machine.
Therefore, if biology is to evolve to environments it isn’t aware of ahead-of-time, then the proper mathematical model is the Universal machine.
My Comments:
1. It is very important to understand what the foregoing argument shows. It doesn’t show that evolution itself is a kind of computation. Nor does it imply that the biosphere is some sort of Universal Turing machine, which generated the dazzling variety of life-forms existing on Earth today.
Rather, what the argument purports to show is that if scientists want to model how evolution works – and in particular, how it can generate new functions without knowing in advance which ones it might be called upon to produce – then they will have to construct a Universal Turing machine, in order to do the job.
2. Does the argument even prove this much? I think not. All it shows is that if you want to explain how natural selection can generate any function, without knowing in advance which one it will be required to create in a given environment, then you will need a Universal Turing machine. But biologists don’t believe that natural selection can generate any function. What they believe is that it can generate some functions, where “some” might well mean: a vanishingly small fraction of the range of all possible functions that could enhance an organism’s fitness in some situations. I made the same point in my review of Dr. Douglas Axe’s book, Undeniable, where I wrote:
Finally, even if Axe’s argument purporting to show that accidental inventions are fantastically improbable were valid, it would still only apply to accidental inventions in general. A much stronger argument is needed to show that each and every accidental invention is fantastically improbable. By definition, the inventions generated by a blind evolutionary process will tend to be the ones whose emergence is most likely: the creme de la creme, which make up only a tiny proportion of all evolutionary targets. For these targets, the likelihood of success may be very low, but not fantastically improbable.
Next, JohnnyB, drawing upon the work of mathematician Stephen Wolfram, introduces a few useful definitions, which distinguish between four different classes of Universal Turing machines:
Stephen Wolfram’s Complexity Classes
Stephen Wolfram classified Turing machines into the following four classes:
Class 1 [Turing] machines [are machines that] tendsed to converge on a single result, no matter what the initial conditions.
Class 2 [Turing] machines [are machines that] give relatively simple and predictable results…
Class 3 [Turing] machines [are machines that give] results that are individually unpredictable, but statistically predictable.
Class 4 [Turing machines are machines that give] results that are not predictable either individually or statistically….
Class 4 systems are the only systems in which Universal computation can occur.
(N.B. Words in brackets were added by me, as a paraphrase of what JohnnyB was saying. Words in blue appear on JohnnyB’s slide, at 15:36 – VJT.)
My Comments:
UPDATE: In a comment below, Tom English has pointed out a serious mistake in the slide above. Readers will note that JohnnyB states that Wolfram classified Turing machines into four classes. This is factually incorrect. Wolfram’s classification is of cellular automata, not Turing machines. Readers can confirm this by consulting this article on cellular automata in the Stanford Encyclopedia of Philosophy – something I should have done myself. I would like to thank Tom English for his correction.
I think the perceptive reader will be able to see where JohnnyB is going here. He’s going to argue that if scientists want to model evolution by natural selection, they’ll have to rely on the most chaotic kind of Universal Turing machines: Class 4 machines, whose results are radically unpredictable.
And now, at last, we come to the nub of JohnnyB’s argument. The numbering below is mine, not JohnnyB’s.
************************************************************************************************
Part Three: JohnnyB’s proof that natural selection is incapable of accounting for Irreducible Complexity
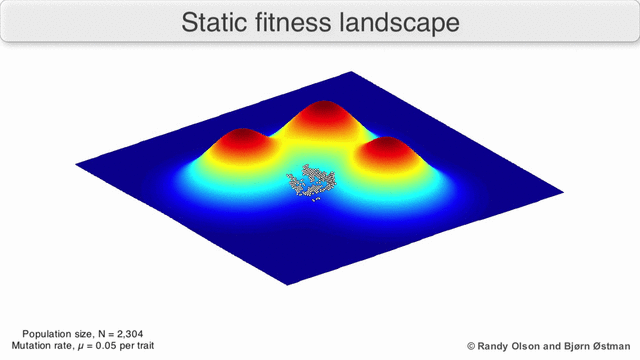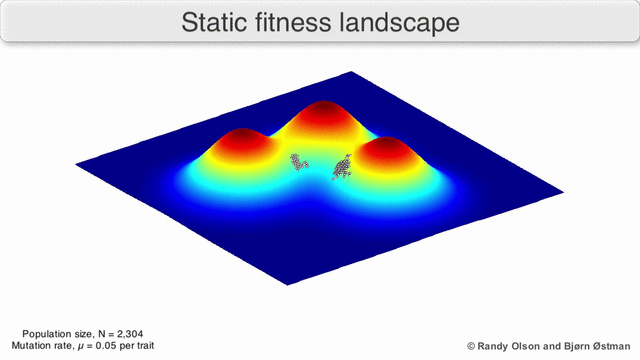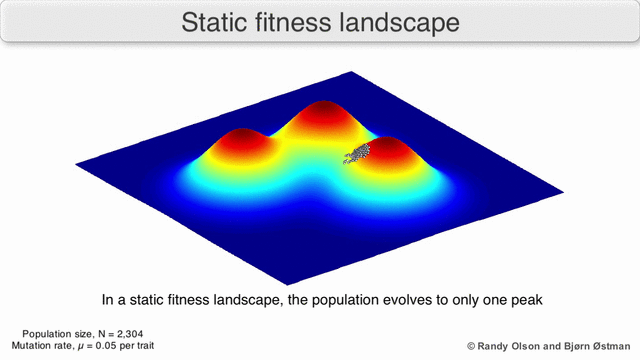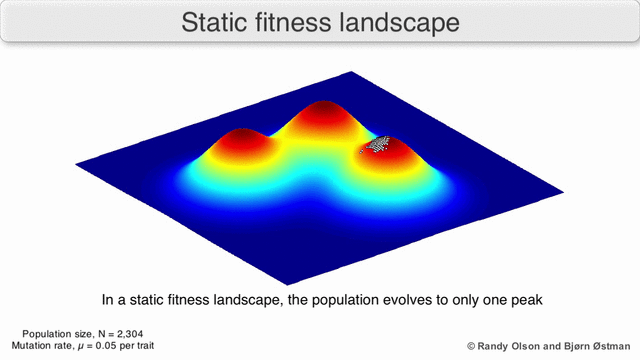
Visualization of a population evolving in a static fitness landscape. Image courtesy of Randy Olson and Bjørn Østman, and Wikipedia.
Universality and Natural Selection
1. Increasing the class [of a Turing machine complexity system – VJT] yields more degrees of freedom, but also makes the relationship more chaotic between changes in input and the resulting output.
2. Class 4 systems are the only systems in which Universal computation can occur.
3. Hidden premise identified by VJT: evolution requires Universal computation.
Proof: see the above slide on Universal vs. Special machines.
4. Therefore, if evolution were to occur, it would need a Class 4 complexity system.
5. For natural selection to operate, there has to be a smooth pathway of increasing function.
[N.B. “Smooth” is defined by JohnnyB as: moving in one direction, without any giant chasms – VJT.]
6. Class 4 systems, since they are chaotic (mappings of input changes to behavior changes are chaotic), cannot in principle supply such a smooth pathway.
7. Thus, the two requirements for evolution – evolution across Universal computation and a selectable pathway – are mutually incompatible.
My Comments:
1. When I looked at this slide, I realized that there was an unstated premise, which I inserted (premise 3). The wording is very important here: in premise 4, JohnnyB states that if evolution were to occur, it would need a Class 4 complexity system. This statement only makes sense if evolution itself is viewed as a computation, and a universal one at that. But as I argued above in Part Two (comment 1), JohnnyB hasn’t shown that. All he’s shown is that if scientists want to model how evolution could give rise to any kind of function, they’ll need a Class 4 Universal Turing machine for the job. That’s what premise 4 should say.
2. Premise 5 simply restates a point commonly made by Intelligent Design advocates: that evolution by natural selection won’t work unless we have a smooth fitness landscape. This requirement sounds very ad hoc, given that we can readily conceive of countless ways in which a fitness landscape might be so rugged as to render evolution by natural selection impossible. So are evolutionists begging the question by assuming that fitness landscapes are smooth, in the real world? Not at all. Professor Joe Felsenstein explains why in a widely quoted post critiquing a talk given by Dr. William Dembski on August 14, 2014, at the Computations in Science Seminar at the University of Chicago, titled, “Conservation of Information in Evolutionary Search.” Felsenstein writes:
Given that there is a random association of genotypes and fitnesses, Dembski is right to assert that it is very hard to make much progress in evolution. The fitness surface is a “white noise” surface that has a vast number of very sharp peaks. Evolution will make progress only until it climbs the nearest peak, and then it will stall. But…
That is a very bad model for real biology, because in that case one mutation is as bad for you as changing all sites in your genome at the same time!
Also, in such a model all parts of the genome interact extremely strongly, much more than they do in real organisms…
…I argue that the ordinary laws of physics actually imply a surface a lot smoother than a random map of sequences to fitnesses. In particular if gene expression is separated in time and space, the genes are much less likely to interact strongly, and the fitness surface will be much smoother than the “white noise” surface.
3. Another point I’d like to make is that evolution doesn’t occur in just two dimensions, but in hundreds of different directions. For this reason, the likelihood of evolution “hitting a wall” beyond which no further improvements can be made is greatly reduced, as computer scientist Mark Chu Carroll noted in a book review published several years ago:
A fitness landscape with two variables forms a three dimensional graph – and in three dimensions, we do frequently see things like hills and valleys. But that’s because a local minimum is the result of an interaction between *only two* variables. In a landscape with 100 dimensions, you *don’t* expect to see such uniformity. You may reach a local maximum in one dimension – but by switching direction, you can find another uphill slope to climb; and when that reaches a maximum, you can find an uphill slope in some *other* direction. High dimensionality means that there are *numerous* directions that you can move within the landscape; and a maximum means that there’s no level or uphill slope in *any* direction.
4. I would also object to Premise 6 in JohnnyB’s argument above. He writes: “Class 4 systems, since they are chaotic (mappings of input changes to behavior changes are chaotic), cannot in principle supply such a smooth pathway.” What he should have said is that Class 4 systems cannot guarantee the existence of a smooth pathway for the evolution of any given function. But all that shows is that some functions (probably the vast majority) will be incapable of evolving. The argument doesn’t show that no smooth pathway exists for any function. I made a similar point in my review of Dr. Douglas Axe’s book, Undeniable:
Axe is perfectly correct in saying that for any given functional hierarchy that we can imagine, most of its components would have been of no benefit earlier on, before the hierarchy had been put together in its present form. But all that proves is that the vast majority of the fantastically large set of possible functional hierarchies never get built in the first place: they are beyond the reach of evolution. If a functional hierarchy was built by evolution, in a series of steps, then by definition, its components must have performed some biologically useful function when the hierarchy had fewer levels than it does now. The functional hierarchies built by evolution are atypical. But that doesn’t make them impossible.
Hence JohnnyB is incorrect when he infers that “the two requirements for evolution – evolution across Universal computation and a selectable pathway – are mutually incompatible.” All his argument shows is that for a large number of possible functions, these two requirements will be incompatible – which means that these functions will never evolve in the first place. But what about the rest?
However, JohnnyB has another ace up his sleeve. As we’ll see, he argues that whenever there is a smooth, non-chaotic pathway which allows a function to evolve, that function can’t be called irreducibly complex, anyway. So it’s still true that irreducibly complex functions could only evolve via a highly unpredictable, chaotic process, making their emergence a practically impossibility.
************************************************************************************************
Part Four: JohnnyB’s Redefinition of Irreducible Complexity, and his Argument for Design

Orson Welles performs a card trick for Carl Sandburg (August 1942). Image courtesy of Wikipedia.
In the argument below, JohnnyB endeavors to show that irreducibly complex systems, properly defined, require an intelligent designer. The numbering below is mine, not JohnnyB’s.
Redefinition of Irreducible Complexity
1. To implement the arbitrary complexity within biology, biological systems must be Class 4 systems.
2. A “hard” problem is a problem for which a solution only exists utilizing the chaotic space of a Class 4 system.
3. If a Class 4 system needs to solve a “hard” problem, it cannot do so by a process of selection, because the chaotic nature of the system will prevent selection from pointing in any specific direction.
4. Therefore, the chance of hitting a correct solution to a “hard” problem is equivalent to that of chance, since selection cannot canalize the results.
[Here’s a short explanation of “canalize,” from the slide titled, “Multilevel Complexity Classes”:
(i) A Class 4 system can be used to create a non-chaotic Class 1 or Class 2 system,for which changes can lead to smoother searches.
(ii) However, this limits the scope of selectable parameters to those which the implemented Class 1 and Class 2 systems operate.
(iii) Thus, we can say that to the extent that evolution occurs, it is parametrized – or “canalized” – VJT.]
5. Information Theory tells us that this will have a difficulty that increases exponentially with the size of the shortest solution.
6. Solutions to “hard” problems can be achieved only if the solution has prior programming which guides either the mutation or the selection through.
7. An Irreducibly Complex system is a system which utilizes (and utilizes necessarily) the chaotic space of a Class 4 system to implement a function.
8. The existence of an Irreducibly Complex system is evidence of design, because design is the only known cause which can navigate the complexity of a Class 4 system to implement functionality.
My Comments:
1. I would criticize the wording of premise 1: “To implement the arbitrary complexity within biology, biological systems must be Class 4 systems.” It should read as follows: “To model the evolution is any kind of function, of any arbitrary level of complexity, scientists must use Class 4 systems.” Once again, JohnnyB is implicitly assuming that the biosphere is a gigantic natural computer, and that evolutionary changes are computations. This only makes sense on a hyper-computationalist view of the world, satirized by the philosopher John Searle in a memorable essay titled, Is the brain a Digital Computer?: “Thus for example the the wall behind my back is right now implementing the Wordstar program, because there is some pattern of molecule movements which is isomorphic with the formal structure of Wordstar.” Against this view, Searle argues that computation is something which is inherently mind-relative:
There is no way you could discover that something is intrinsically a digital computer because the characterization of it as a digital computer is always relative to an observer who assigns a syntactical interpretation to the purely physical features of the system… [T] to say that something is functioning as a computational process is to say something more than that a pattern of physical events is occurring. It requires the assignment of a computational interpretation by some agent.
2. Premise 2 is the critical one in JohnnyB’s argument. He defines a “hard” problem as one that can only be solved within the chaotic space of a Class 4 system, and he goes on to argue in premise 7 that an irreducibly complex system is one whose generation requires the solution of a “hard” problem: “An Irreducibly Complex system is a system which utilizes (and utilizes necessarily) the chaotic space of a Class 4 system to implement a function.” As we’ll see, JohnnyB thinks that only a designer is capable of finding such a solution.
The problem with this approach is that while it may (if the reasoning proves to be correct) establish that intelligent design is required in order to generate irreducibly complex systems, what it does not show is that any such systems actually exist in Nature. Perhaps the bacterial flagellum, for instance, can be solved within a more restricted, non-chaotic space. JohnnyB cannot rule out such a possibility, for he writes that “to the extent that evolution occurs, it is parametrized” – i.e. “canalized.” At least some evolution occurs in Nature. Who is to say, then, that “canalized” evolution could not possibly give rise to a bacterial flagellum, over a period of aeons?
3. Premises 4 and 5 completely undermine the goal of JohnnyB’s presentation. Premise 4 states that “the chance of hitting a correct solution to a ‘hard’ problem is equivalent to that of chance,” and premise 5 adds that the degree of difficulty for a “hard” problem “increases exponentially with the size of the shortest solution.” But in the Goals section at the beginning of his talk, JohnnyB declared that he was trying to “create a definition of Irreducible Complexity which shows that Darwinism is logically impossible over a wide range of assumptions.” There’s a vast philosophical difference between logically impossible and exponentially improbable.
4. I might also add that “chance” and “chaos” are two entirely different concepts. A chaotic system is radically unpredictable; a system whose processes are governed by chance may still be statistically predictable. The reason why I mention this here is that I argued above that random genetic drift might be able to account for the evolution of some irreducibly complex systems. But this chance process, if it took place, would not have been a totally chaotic one. If it had been, then the systems would almost certainly never have evolved in the first place.
5. Premise 6, which says that “hard” problems can only be solved by “prior programming,” does not warrant the conclusion that an Irreducibly Complex system is evidence of design. The fact that design is the only known cause of some irreducibly complex systems (with which we are familiar) does not imply that design is able to create any irreducibly complex system, of an arbitrarily high degree of complexity. For all we know, there might be systems which are beyond the reach of any designer, because they’re too complex for anyone to model. This is important, for as the eminent chemist Professor James Tour points out, in his 2016 talk, The Origin of Life: An Inside Story, life itself is fiendishly complex. And what makes the puzzle of life’s origin all the more baffling is that even if you had a “Dream Team” of brilliant chemists and gave them all the ingredients they wanted, they would still have no idea how to assemble a simple cell. In Tour’s words:
All right, now let’s assemble the Dream Team. We’ve got good professors here, so let’s assemble the Dream Team. Let’s further assume that the world’s top 100 synthetic chemists, top 100 biochemists and top 100 evolutionary biologists combined forces into a limitlessly funded Dream Team. The Dream Team has all the carbohydrates, lipids, amino acids and nucleic acids stored in freezers in their laboratories… All of them are in 100% enantiomer purity. [Let’s] even give the team all the reagents they wish, the most advanced laboratories, and the analytical facilities, and complete scientific literature, and synthetic and natural non-living coupling agents. Mobilize the Dream Team to assemble the building blocks into a living system – nothing complex, just a single cell. The members scratch their heads and walk away, frustrated…
So let’s help the Dream Team out by providing the polymerized forms: polypeptides, all the enzymes they desire, the polysaccharides, DNA and RNA in any sequence they desire, cleanly assembled. The level of sophistication in even the simplest of possible living cells is so chemically complex that we are even more clueless now than with anything discussed regarding prebiotic chemistry or macroevolution. The Dream Team will not know where to start. Moving all this off Earth does not solve the problem, because our physical laws are universal.
You see the problem for the chemists? Welcome to my world. This is what I’m confronted with, every day.
So it seems that we have a Mexican standoff. It seems that JohnnyB would have to agree that the first living cell must have contained one or more irreducibly complex systems. That being the case, its evolution via unguided processes would have been extraordinarily unlikely, if JohnnyB’s argument is successful. But as Professor James Tour points out, our top designers are incapable of creating such a cell, either. So what produced it? We are left without an answer.
************************************************************************************************
Part Five: JohnnyB’s criticisms of Avida
Avida Checklist
Is the programming language of Avida a Class 4 system? Yes.
Do any of the evolved Avida programs require the use of chaotic spaces in the Class 4 system? No.
Therefore, the evolved Avida programs are not Irreducibly complex.
My Comments:
I know very little about Avida, so I’ll keep my comments brief. What I will say is that JohnnyB’s reasoning above sounds quite similar in thought and tone to a piece that Winston Ewert wrote on the subject of Avida, back in 2014:
What Avida demonstrates is that given a gradual slope, Darwinian processes are capable of climbing it. What irreducible complexity claims is that irreducible complex systems are surrounded on all sides by cliffs. Notice the distinction. Avida says that evolution can climb gradual slopes. Irreducible complexity claims that there are no gradual slopes. Avida is about what we can do with the gradual slopes, and irreducibly complexity is about whether or not the slopes exist. Avida provides no evidence that gradual slopes exist, it just assumes that they do. What Avida demonstrates is simply beside the point of the claim of irreducible complexity. (Emphasis mine – VJT.)
Winston Ewert’s statement that “Irreducible complexity claims that there are no gradual slopes” is basically equivalent to JohnnyB’s claim that irreducibly complex systems require the use of chaotic spaces in a Class 4 system. I have critiqued above (see Part Three, comment 2) the claim that evolution requires a smooth fitness landscape, as an argument for design.
Conclusion
As I see it, JohnnyB’s presentation on irreducible complexity, while far more mathematically rigorous than anything I have seen previously in the Intelligent Design literature, suffers from several major problems:
(i) it completely overlooks non-Darwinian naturalistic mechanisms for the evolution of irreducibly complex systems;
(ii) it commits the “pan-computationalist” fallacy, by treating the biosphere itself as if it were one vast computational system, and equates this system with a Class 4 Universal Turing machine, whose outputs (or results) are radically unpredictable (i.e. chaotic);
(iii) all it shows is that scientists would require such a machine, if they wanted to demonstrate that evolution was capable of generating any kind of function, no matter how complex;
(iv) smooth fitness landscapes are a fairly straightforward consequence of physics in our universe, at any rate – and what’s more, since evolution proceeds in not two but hundreds of different directions at once, the likelihood of evolution getting stuck at some local maximum is very low;
(v) in any case, Class 4 systems are not always chaotic in their behavior – which means that there may well be some complex structures in living things that could have evolved as a result of processes occurring outside the “chaotic space” of radical unpredictability;
(vi) arbitrarily redefining “irreducibly complex systems” as those systems whose evolution would have had to take place within the “chaotic space” of a Class 4 system is no way to safeguard the Argument from Design, because one still needs to show that there are any such systems in Nature, and that the systems which ID advocates consider to be designed could only have evolved in a chaotic fashion, if they evolved at all;
(vii) finally, it has not been shown that there exists an Intelligent Designer Who is capable of creating irreducibly complex systems of an arbitrarily high level of complexity – such as we find in even the simplest living cell. As we’ve seen, not even all the world’s scientists working together would have any idea how to create such a cell. As far as we know, then, intelligence is inadequate for the task of creating life. There may, of course, be some Super-Agent that was capable of creating the first life. But the argument from irreducible complexity, taken by itself, gives us no reason to think that.
I would like to conclude by saying that on an intuitive level, I feel the force of the design argument as much as anyone, and I am quite sure that the first cell was in fact designed – as well as many other complex structures we find in Nature. (How they were designed is another question entirely, on which I try to keep an open mind.) But if I am asked whether it has been rigorously demonstrated that the molecular machines we find within the cell were intelligently designed, I would have to answer in the negative. At the present time, I am inclined to think that the best argument for design is a multi-pronged one, which makes use of several converging lines of evidence.
What do readers think of JohnnyB’s argument? Over to you – and JohnnyB!

What evidence do you have of anything else happening?*
See, empiricists are sort of stuck with the evidence. IDists, not so much.
Being limited to the evidence is actually a good thing.
Glen Davidson
*Other than “natural selection,” of course.
GlenDavidson,
What evidence do you have that a species transition is random?
What do we have evidence of happening?
And I didn’t say that species transitions are necessarily random (although I suspect that enough speciation is due to drift), as you had mentioned “adaption.” Conveniently, you ignore that for the sake of your manufactured strawman.
Glen Davidson
I’d love to hear more about the plan and your understanding of it. What’s it all about?
GlenDavidson,
I’m sure you know that the lumped effects of unidentified factors are modeled as random. Modelers are generally not saying that the effects are due to chance. For instance, if I say that the impact point of a bullet follows a Gaussian distribution, with the aim point as the mean, I am not saying that something other than classical (deterministic) mechanics governs the outcome.
I don’t know what the side-discussion of Theobald is about. Perhaps he has said, as I’m saying now, that the metaphysical question of whether variation in offspring is “really random” does not matter in evolutionary biology. What does matter is that the variation in offspring is not systematically related to fitness — the propensity of a type to leave offspring.
Religious objectors to evolution usually goad themselves along with the words chance and random. The standard response is to say that selection is deterministic. But I think we should say instead that evolutionary biology does not require that anything occur by chance.
There just is a number of meanings of “chance” and similar terms.
To be sure, the beauty of evolutionary theory is that it isn’t “just chance.” This includes mutations, although they seem “random with respect to fitness.”
Glen Davidson
I agree with the description of “random” processes in scientific theories as being models of reality that may or may not actually be random. Whether or not it is actually random is irrelevant to the use of those models.
The question arises: do those who object to using random processes as models go so far as to object to assuming random Mendelian segregation? Assuming random movement in Brownian Motion? Do they feel that one has built in unacceptable assumptions about reality when one does those?
Theists can’t be the product of random replication “mistakes”. They just can’t live with that thought. They MUST be made in the image of a deity, and own the entire universe which must have been created especially for them. Doesn’t get much more arrogant than that
That’s only apparent arrogance. They’re really humble. Humility is a virtue, after all.
OMagain,
It is about as clear as my understanding of the origin of the hydrogen atom 🙂
Not a huge amount of entertainment value in pursuing the semantic, but theists tend not to mean ‘random in opposition to deterministic’. They tend to mean ‘random in opposition to someone having an aim’.
My thoughts on Allan Miller’s thoughts on vjtorley’s thoughts on JohnnyB’s new view of Irreducible Complexity.
def random_thoughts(thoughts)
return thoughts.determined
end
ETA: should have added a check for thoughts.nil?
But too late for that now!
Mung,
My thoughts, just to get the chain right, were on colewd’s thoughts on something somewhat unrelated to either OP.
Verdict first, evidence TBA.
There are a zillion variations on theology, but but when you back a theist into a corner, the non-negotiable last and final stand is: This is the planned of all possible worlds.
Off topic:
I have my post: “How did the Designer/God do it? How was life created?” ready but I just noticed that my previous post “The embarrassing “science” of the origins of life: The missing piece of evidence that persuaded scientists to believe in abiogenesis” is still pending approval since April 15…
How long does it take for a post to be approved? More than 2 weeks? Or…the reason why it has not been approved yet is more than just related to taking time to approve it…
The motto of this blog is apparently about the possibilities of being mistaken…right?
“I beseech you, in the bowels of Christ, think it possible that you may be mistaken.”
So, let it be such!
Generally, it takes until you post a request, preferable in the moderation thread.
I’ve published the “embarrassing” thread, since that seems older. If you want me to publish the other right now, just say so. Otherwise I’ll wait till tomorrow.
Neil Rickert,
I don’t know what I mean by older??? I submitted it for publishing 2 weeks ago. Why would you think it was older whatever that meant?
J-Mac,
I was just going by your words, which seemed to imply that it had been waiting longer.
I could spend every waking minute looking to see if there is a pending post. Or I could just wait until someone asks. Guess which I choose. And the other moderators (all of whom are unpaid) seem to make the same choice.