Recent discussions of genetic algorithms here and Dave Thomas’ evisceration of Winston Ewert’s review of several genetic algorithms at The Panda’s Thumb prompted me to dust off my notes and ev implementation.
Introduction
In the spring of 1984, Thomas Schneider submitted his Ph.D thesis demonstrating that the information content of DNA binding sites closely approximates the information required to identify the sites in the genome. In the week between submitting his thesis and defending it, he wrote a software simulation to confirm that the behavior he observed in biological organisms could arise from a subset of known evolutionary mechanisms. Specifically, starting from a completely random population, he used only point mutations and simple fitness-based selection to create the next generation.
The function of ev is to explain and model an observation about natural systems.
— Thomas D. Schneider
Even with this grossly simplified version of evolution, Schneider’s simulator, tersely named ev, demonstrated that the information content of a DNA binding site, ![]() , consistently and relatively quickly evolves to be approximately equal to the information required to identify the binding sites in a given genome,
, consistently and relatively quickly evolves to be approximately equal to the information required to identify the binding sites in a given genome, ![]() , just as is seen in the biological systems that were the subject of his thesis.
, just as is seen in the biological systems that were the subject of his thesis.
Schneider didn’t publish the details of ev until 2000, in response to creationist claims that evolution is incapable of generating information.
Core Concepts
Before discussing the implementation, it’s important to understand exactly what is being simulated. Dr. Schneider’s thesis is quite readable. The core concepts of ev are binding sites, ![]() , and
, and ![]() .
.
Binding Sites
A binding site is a location on a strand of DNA or RNA where a protein can attach (bind). Binding sites consist of a sequence of nucleotides that together provide the necessary chemical bonds to hold the protein.
A good example of binding sites in action is the synthesis of messenger RNA (mRNA) by RNA polymerase (RNAP). RNAP binds to a set of a few tens of base pairs on a DNA strand which triggers a series of chemical reactions that result in mRNA. This mRNA is then picked up by a ribosome (which also attaches to a binding site) that transcribes a protein from it.
The bases that make up a binding site are best described by a probability distribution, they are not a fixed set requiring an exact match.
![]() is the simplest of the two information measures in ev. Basically, it is the number of bits required to find one binding site out of set of binding sites in a genome of a certain length. For a genome of length
is the simplest of the two information measures in ev. Basically, it is the number of bits required to find one binding site out of set of binding sites in a genome of a certain length. For a genome of length ![]() with
with ![]() binding sites, this is
binding sites, this is ![]()
For example, consider a genome of 1000 base pairs containing 5 binding sites. The average distance between binding sites is 200 bases, so the information needed to find them is ![]() which is approximately 7.64 bits.
which is approximately 7.64 bits.
![]() is the amount of information in the binding site itself. There are two problems with computing
is the amount of information in the binding site itself. There are two problems with computing ![]() . The first is the definition of “information.” Schneider uses Shannon information, a clearly defined, well-respected metric with demonstrated utility in the study of biological systems.
. The first is the definition of “information.” Schneider uses Shannon information, a clearly defined, well-respected metric with demonstrated utility in the study of biological systems.
The second problem is that binding sites for the same protein don’t consist of exactly the same sequence of bases. Aligned sequences are frequently used to identify the bases that are most common at each location in the binding site, but they don’t tell the whole story. An aligned sequence that shows an A in the first position may reflect a set of actual sites of which 70% have A in the first position, 25% C, and 5% G. ![]() must take into account this distribution.
must take into account this distribution.
The Shannon uncertainty of a base in a binding site is:
(1) 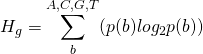
where ![]() is the probability of a base
is the probability of a base ![]() at that location in the genome. This will be approximately 0.25, equal probability for all bases, for the initial, randomly generated genome. The initial uncertainty at a binding site is therefore:
at that location in the genome. This will be approximately 0.25, equal probability for all bases, for the initial, randomly generated genome. The initial uncertainty at a binding site is therefore:
(2) ![]()
where ![]() is the width of the site.
is the width of the site.
![]() , the increase in information, is then
, the increase in information, is then ![]() , where:
, where:
(3) 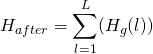
computed from the observed probabilities.
There is one additional complexity with these formulas. Because of the small sample size, an adjustment must be computed for ![]() :
:
(4) 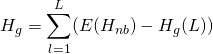
or
(5) 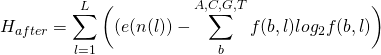
measured in bits per site.
The math behind the small sample adjustment is explained in Appendix 1 of Schneider’s thesis. Approximate values for ![]() for binding site widths from 1 to 50 are available pre-computed by a program available on Schneider’s site:
for binding site widths from 1 to 50 are available pre-computed by a program available on Schneider’s site:
For a random sequence, ![]() will be near 0. This will evolve to
will be near 0. This will evolve to ![]() over an ev run.
over an ev run.
Schneider’s ev Implementation
Schneider’s implementation is a fairly standard genetic algorithm, with an interesting fitness function. The virtual genomes contain, by default, 256 potential binding sites. The genomes are composed of characters from an alphabet of four letters (A, C, G, and T). The default number of optimal binding sites, ![]() , is 16. The locations of these sites are randomly generated at the beginning of each run and remain the same throughout the run. Given this configuration,
, is 16. The locations of these sites are randomly generated at the beginning of each run and remain the same throughout the run. Given this configuration, ![]() , the amount of information required to identify one of these sites in a genome of length
, the amount of information required to identify one of these sites in a genome of length ![]() is
is ![]() which equals 4. Per Schneider’s Ph.D thesis,
which equals 4. Per Schneider’s Ph.D thesis, ![]() , the information in the binding site itself, should evolve to and remain at approximately this value during a run.
, the information in the binding site itself, should evolve to and remain at approximately this value during a run.
To determine the number of binding sites actually present, a portion of the genome codes for a recognizer as well as being part of the set of potential binding sites. This recognizer, which is subject to the same mutation and selection as the rest of the genome, is applied at each base to determine if that base is the start of a binding site. If a base is not correctly identified as the start of a binding site, the fitness of the genome is decreased by one. If a base is incorrectly identified as the start of a binding site, the fitness of the genome is also decreased by one. Schneider notes that changing this weighting may affect the rate at which ![]() converges to
converges to ![]() but not the final result.
but not the final result.
After all genomes are evaluated, the half with the lowest fitness are eliminated and the remaining are duplicated with mutation. Schneider uses a relatively small population size of 64.
The recognizer is encoded as a weight matrix of ![]() two’s-complement integers, where
two’s-complement integers, where ![]() is the length of a binding site (6 by default). Schneider notes that:
is the length of a binding site (6 by default). Schneider notes that:
At first it may seem that this is insufficient to simulate the complex processes of transcription, translation, protein folding and DNA sequence recognition found in cells. However the success of the simulation, as shown below, demonstrates that the form of the genetic apparatus does not affect the computed information measures. For information theorists and physicists this emergent mesoscopic property will come as no surprise because information theory is extremely general and does not depend on the physical mechanism. It applies equally well to telephone conversations, telegraph signals, music and molecular biology.
Since ev genomes consist only of A, C, G, and T, these need to be translated to integers for the weight matrix. Schneider uses the straightforward mapping of (A, C, G, T) to (00, 01, 10, 11). The default number of bases for each integer is ![]() . Given these settings, AAAAA encodes the value 0, AAAAC encodes 1, and TTTTT encodes -1 (by two’s-complement rules).
. Given these settings, AAAAA encodes the value 0, AAAAC encodes 1, and TTTTT encodes -1 (by two’s-complement rules).
When evaluating a genome, the first ![]() bases are read into the
bases are read into the ![]() weight matrix. The next
weight matrix. The next ![]() bases represent a threshold value that is used to determine whether or not the value returned by the recognizer is a binding site match. This is also a two’s-complement integer with the same mapping. The recognizer is then applied from the first base in the genome to the last that could possibly be the start of a binding site (given the binding site length).
bases represent a threshold value that is used to determine whether or not the value returned by the recognizer is a binding site match. This is also a two’s-complement integer with the same mapping. The recognizer is then applied from the first base in the genome to the last that could possibly be the start of a binding site (given the binding site length).
It’s worth re-emphasizing that the recognizer and the threshold are part of the genome containing the binding sites. The length of the full genome is therefore ![]() bases, with only the first
bases, with only the first ![]() bases being potential binding sites.
bases being potential binding sites.
The recognizer calculates a total value for the potential site starting at a given point by summing the values of the matching bases in the weight matrix. The weight matrix contains a value for each base at each position in the site, so for a binding site length of 7 and a potential binding site consisting of the bases GATTACA, the total value is:
w[0]['G'] + w[1]['A'] + w[2]['T'] + w[3]['T'] + w[4]['A'] + w[5]['C'] + w[6]['A']
If this value exceeds the threshold, the recognizer identifies the bases as a binding site.
This implementation of the recognizer is an interesting way of encapsulating the biological reality that binding sites don’t always consist of exactly the same sequence of bases. Schneider notes, though, that “the exact form of the recognition mechanism is immaterial because of the generality of information theory.”
Schneider’s Results
Using his default settings of:
- Genome length:

- Number of binding sites:

- Binding site length:

- Bases per integer:

Schneider found that:
When the program starts, the genomes all contain random sequence, and the information content of the binding sites,
, is close to zero. Remarkably, the cyclic mutation and selection process leads to an organism that makes no mistakes in only 704 generations (Fig. 2a). Although the sites can contain a maximum of
bits, the information content of the binding sites rises during this time until it oscillates around the predicted information content,
bits . . . .
The Creationist Response
30 years after the original implantation and 16 years after it was published, Intelligent Design Creationists (IDCists) are still attempting to refute ev and are still getting it wrong.
Dembski In 2001
In 2001, William Dembski claimed that ev does not demonstrate an information increase and further claimed that Schneider “smuggled in” information via his rule for handling ties in fitness. Schneider reviewed and rebutted the first claim and tested Dembski’s second claim, conclusively demonstrating it to be false.
Schneider wryly addresses this in the ev FAQ:
Does the Special Rule smuggle information into the ev program?
This claim, by William Dembski, is answered in the on-line paper Effect of Ties on the evolution of Information by the ev program. Basically, changing the rule still gives an information gain, so Dembski’s prediction was wrong.
Has Dembski ever acknowledged this error?
Not to my knowledge.
Don’t scientists admit their errors?
Generally, yes, by publishing a retraction explaining what happened.
Montanez, Ewert, Dembski, and Marks In 2010
Montanez, Ewert, Dembski, and Marks published A Vivisection of the ev Computer Organism: Identifying Sources of Active Information in the IDCist’s pseudo-science journal BIO-Complexity in 2010. Despite its title, the paper doesn’t demonstrate any understanding of the ev algorithm or what it demonstrates:
- The authors spend a significant portion of the paper discussing the efficiency of the ev algorithm. This is a red herring — nature is profligate and no biologist, including Schneider, claims that evolutionary mechanisms are the most efficient way of achieving the results observed.
- Related to the efficiency misdirection, the authors suggest alternative algorithms that have no biological relevance instead of addressing the actual algorithm used by ev.
- The authors do not use Shannon information, instead substituting their idiosyncratic “active information”, including dependencies on Dembski’s concept of “Conservation of Information” which has been debunked by Wesley Elsberry and Jeffrey Shallit in Information Theory, Evolutionary Computation, and Dembski’s “Complex Specified Information”, among others.
- The authors note that “A common source of active information is a software oracle”. By recognizing that an oracle enables evolutionary mechanisms to work in software, they are admitting that those same mechanisms can explain what we observe in biological systems because the real world environment is just such an oracle. The environment provides information about what works and what doesn’t by ensuring that organisms less suited to it will tend to leave fewer descendants.
- The authors repeatedly claim that the “perceptron” used as a recognizer makes the ev algorithm more efficient. Their attempted explanation of why this is the case completely ignores the actual implementation of ev. They seem so caught up in Schneider’s description of the recognizer as a perceptron that they miss the fact that it’s nothing more than a weight matrix that models the biological reality that a binding site is not a fixed set of bases.
Basically the paper is a rehash of concepts the authors have discussed in previous papers combined with the hope that some of it will be applicable to ev. None of it is.
Schneider soundly refuted the paper in Dissection of “A Vivisection of the ev Computer Organism: Identifying Sources of Active Information”. He succinctly summarized the utter failure of the authors to address the most important feature of ev:
They do not compute the information in the binding sites. So they didn’t evaluate the relevant information (
) at all.
In a response to that refutation, Marks concedes that “Regardless, while we may have different preferred techniques for measuring information, we agree that the ev genome does in fact gain information.”
After that damning admission, Marks still doubles down on his spurious claim that the “Hamming oracle” makes ev more efficient:
Schneider addresses the hamming oracle issue by assuming that nature provides a correct fitness function (a hamming function) that allows for positive selection in the direction of our target. He argues that this fitness is based on a
biologically sensible criteria: having functional DNA binding sites and not having extra ones.
But this describes a target; this is the desired goal of the simulation. The fitness function actually being used is a distance to this target. This distance makes efficient information extraction possible.
That’s not a target. It provides no details about what a solution would look like or how to reduce the distance measured, it simply indicates how far away a genome is from being a solution. In fact, it does less than that because it doesn’t provide any information about the difference between an existing recognizer and an ideal recognizer. It also says nothing at all about the relationship between ![]() and
and ![]() .
.
Even as he tries to salvage the tatters of his paper, Marks makes another concession:
Reaching that point requires a particular shape to the fitness landscape to guide evolution.
He admits again that evolution does work in certain environments. The real world is one of those.
Nothing in Marks’ response changes the accuracy of Schneider’s summary in his refutation:
Aside from their propensity to veer away from the actual biological situation, the main flaw in this paper is the apparent misunderstanding of what ev is doing, namely what information is being measured and that there are two different measures. The authors only worked with
and ignored
. They apparently didn’t compute information from the sequences. But it is the increase of
that is of primary importance to understand. Thanks to Chris Adami, we clearly understand that information gained in genomes reflects ‘information’ in the environment. I put environmental ‘information’ in quotes because it is not clear that information is meaningful when entirely outside the context of a living organism. An organism interprets its surroundings and that ‘information’ guides the evolution of its genome.
Ewert in 2014
Winston Ewert published Digital Irreducible Complexity: A Survey of Irreducible Complexity in Computer Simulations in 2014, again in the IDCists’ house journal BIO-Complexity. This paper constituted 25% of the output of that august publication in that year. Ewert reviewed Avida, ev, Dave Thomas’ Steiner Trees, a geometric algorithm by Suzanne Sadedin, and Adrian Thompson’s Digital Ears, attempting to demonstrate that none of them generated irreducible complexity.
Michael Behe defined “irreducible complexity” in his 1996 book Darwin’s Black Box:
By irreducibly complex I mean a single system composed of several well-matched, interacting parts that contribute to the basic function, wherein the removal of any one of the parts causes the system to effectively cease functioning. An irreducibly complex system cannot be produced directly (that is, by continuously improving the initial function, which continues to work by the same mechanism) by slight, successive modifications of a precursor system, because any precursor to an irreducibly complex system that is missing a part is by definition nonfunctional.
Dave Thomas has shredded Ewert’s discussion of Steiner Trees, demonstrating that Ewert addressed a much simpler problem (spanning trees) instead.
Richard B. Hoppe has similarly destroyed Ewert’s claims about Avida.
Schneider does explicitly claim that ev demonstrates the evolution of irreducible complexity:
The ev model can also be used to succinctly address two other creationist arguments. First, the recognizer gene and its binding sites co-evolve, so they become dependent on each other and destructive mutations in either immediately lead to elimination of the organism. This situation fits Behe’s definition of ‘irreducible complexity’ exactly . . . .
Ewert quotes this claim and attempts to refute it with:
It appears that Schneider has misunderstood the definition of irreducible complexity. Elimination of the organism would appear to refer to being killed by the model’s analogue to natural selection. Given destructive mutations, an organism will perform less well than its competitors and “die.” However, this is not what irreducible complexity is referring to by “effectively ceasing to function.” It is true that in death, an organism certainly ceases to function. However, Behe’s requirement is that:
If one removes a part of a clearly defined, irreducibly complex system, the system itself immediately and necessarily ceases to function.
The system must cease to function purely by virtue of the missing part, not by virtue of selection.
It appears that Ewert is the one with the misunderstanding here. If there is a destructive mutation in the genes that code for the recognizer, none of the binding sites will be recognized and, in the biological systems that ev models, the protein will not bind and the resulting capability will not be provided. It will “immediately and necessarily” cease to function. This makes the system irreducibly complex by Behe’s definition.
Binding sites are somewhat less brittle, simply because there are more of them. However, if there is a destructive mutation in one or more of the binding sites, the organism with that mutation will be less fit than others in the same population. In a real biological system, the function provided by the protein binding will be degraded at best and eliminated at worst. The organism will have effectively ceased to function. It is this lack of function that results in the genome being removed from the gene pool in the next generation.
Given that the recognizer and binding sites form a set of “well-matched, interacting parts that contribute to the basic function” and that “the removal of any one of the parts causes the system to effectively cease functioning”, ev meets Behe’s definition of an irreducibly complex system.
The IDCist Discovery Institute touted Ewert’s paper as evidence of “an Excellent Decade for Intelligent Design” in the ten years following the Dover trial. That case, of course, is the one that showed conclusively that ID is simply another variant of creationism and a transparent attempt to violate the separation of church and state in the United States. If Ewert’s paper is among the top achievements of the IDC movement in the past ten years then it’s clear that reality-based observers still have no reason to take any IDCist pretensions to scientific credibility seriously. The political threat posed by intelligent design and other variants of creationism is, unfortunately, still a significant problem.
An Alternative ev Implementation
I have implemented a variant of Dr. Schneider’s ev in order to reproduce his results and explore the impact of some alternative approaches. My version of ev uses the GA Engine I wrote to solve Dave Thomas’ Steiner Network design challenge. This engine operates on bit strings rather than the characters used by Dr. Schneider’s implementation.
As described in the GA engine documentation, applying the GA engine to a problem consists of following a few simple steps:
- Create a class to represent the characteristics of the problem
The problem class
ev-problemcontains the parameters for genome length ( ), number of binding sites (
), number of binding sites ( ), binding site length (
), binding site length ( ), and bases per integer (
), and bases per integer ( ).
). - Implement a method to create instances of the problem class
The
make-ev-problemfunction creates an instance ofev-problem. - Implement the required generic functions for the problem:
genome-length
The genome length is
 , using two bits to encode each base pair.
, using two bits to encode each base pair.fitness
The fitness of a genome is the number of mistakes made by the recognizer, the total of missed and spurious binding sites.
fitness-comparator
This problem uses the
greater-comparatorprovided by the GA engine. - Implement a
terminatorfunctionThis problem uses the
generation-terminatorprovided by the GA engine, stopping after a specified number of generations. - Run
solve
Initial Results
In my implementation, Schneider’s default settings and selection mechanism are configured like this:
(defparameter *default-ev-problem*
(make-ev-problem 256 16 6 5))
(let* ((problem *default-ev-problem*)
(gene-pool (solve problem 64 (generation-terminator 3000)
:selection-method :truncation-selection
:mutation-count 1
:mutate-parents t
:interim-result-writer #'ev-interim-result-writer))
(best-genome (most-fit-genome gene-pool (fitness-comparator problem))))
(format t "~%Best = ~F~%Average = ~F~%~%"
(fitness problem best-genome)
(average-fitness problem gene-pool)))This creates an instance of the ev-problem with 256 potential binding sites, 16 actual binding sites, a binding site width of 6 bases, and 5 bases per integer. It then evolves this population for 3000 generations using truncation selection (taking the top 50% of each gene pool to seed the next generation), changing one base in each genome, including the parent genomes, per generation.
The results are identical to those reported by Schneider. Over ten runs, each with a different random seed, the population evolves to have at least one member with no mistakes within 533 to 2324 generations (the mean was 1243.6 with a standard deviation of 570.91). ![]() approaches
approaches ![]() throughout this time. As maximally fit genomes take over the population,
throughout this time. As maximally fit genomes take over the population, ![]() oscillates around
oscillates around ![]() .
.
While my implementation lacks the GUI provided by Schneider’s Java version, the ![]() values output by
values output by ev-interim-result-writer show a similar distribution.
Variations
There are many configuration dimensions that can be explored with ev. I tested a few, including the effect of population size, selection method, mutation rate, and some problem-specific parameters.
Population Size
Increasing the population size from 64 to 256 but leaving the rest of the settings the same reduces the number of generations required to produce a maximally fit genome to between 251 and 2255 with a mean of 962.23 and a standard deviation of 792.11. A population size of 1000 results in a range of 293 to 2247 generations with a lower mean (779.4) and standard deviation (689.68), at a higher computation cost.
Selection Method
Schneider’s ev implementation uses truncation selection, using the top 50% of a population to seed the next generation. Using tournament selection with a population of 250, a tournament size of 50, and a mutation rate of 0.5% results in a maximally fit individual arising within 311 to 4561 generations (with a mean of 2529.9 and standard deviation of 1509.01). Increasing the population size to 500 gives a range of 262 to 4143 with a mean of 1441.2 and standard deviation of 1091.95.
Adding crossover to tournament selection with the other parameters remaining the same does not seem to significantly change the convergence rate.
Changing the tournament selection to mutate the parents as well as the children of the next generation does, however, have a significant impact. Using the same population size of 500 and mutation rate of 0.5% but mutating the parents results in a maximally fit individual within 114 to 1455 generations, with a mean of 534.1 and a standard deviation of 412.01.
Roulette wheel selection took much longer to converge, probably due to the fact that a large percentage of random genomes have identical fitness because no binding sites, real or spurious, are matched. This makes the areas of the wheel nearly equal for all genomes in a population.
Mutation Rate
In the original ev, exactly one base of 261 in each genome is modified per generation. This explores the fitness space immediately adjacent to the genome and is essentially simple hill climbing. This mutation rate is approximately 0.2% when applied to a string of bases represented by two bits each.
Changing the mutation count to a mutation rate of 1% results in ev taking an order of magnitude more generations to produce a maximally fit individual. Rates of 0.5% and 0.2% result in convergence periods closer to those seen with a single mutation per genome, both with truncation and tournament selection, particularly with larger population sizes. As Schneider notes, this is only about ten times the mutation rate of HIV-1 reverse transcriptase.
Binding Site Overlap
By default, binding sites are selected to be separated by at least the binding site width. When this restriction is removed, surprisingly the number of generations required to produce the first maximally fit genome ranges does not change significantly from the non-overlapping case.
Alternative Implementation Results
Population size seems to have the largest impact on the number of generations required to reach equilibrium. Mutation rate has a smaller effect, but can prevent convergence when set too high. Tournament selection takes a bit longer to converge than truncation selection, but the two are within the same order of magnitude. Roulette selection does not work well for this problem.
Unlike the Steiner network and some other problems, crossover doesn’t increase the convergence rate. Mutating the parent genomes before adding them to the next generation’s gene pool does have a measurable impact.
Regardless of selection method, mutation rate, or other parameters, ![]() always evolves to and then oscillates around
always evolves to and then oscillates around ![]() .
.
Source Code
The code is available on GitHub. The required files are:
ga-package.lispga.lispexamples/ga-ev-package.lispexamples/ga-ev.lispexamples/load-ev.lisp
To run from the command line, make the examples directory your working directory and then call
ccl64 - -load load-ev.lisp`
if you’re using Clozure CL or
sbcl - -load load-ev.lisp`
if you’re using Steel Bank Common Lisp.
If you need a refresher on Common Lisp programming, Peter Seibel’s Practical Common Lisp is an excellent book.
Summary
In addition to being a good test case for evolutionary algorithms, ev is interesting because of its biological relevance. As Schneider points out in his Results section:
Although the sites can contain a maximum of
bits, the information content of the binding sites rises during this time until it oscillates around the predicted information content
bits, with
bits during the 1000 to 2000 generation interval.
With this, ev sticks a spoke in the tires of creationists who complain that GAs like Richard Dawkins’ weasel program only demonstrate “directed evolution”. There is nothing in the ev implementation that requires that ![]() evolve to
evolve to ![]() , yet it does every time.
, yet it does every time.
It’s well worth running the Java version of ev to see the recognizer, threshold, and binding sites all co-evolving. This is a clear answer to creationist objections about how “irreducibly complex” parts could evolve.
The common creationist argument from incredulity based on the complexity of cell biochemistry is also touched on by ev. Even with a genome where the recognizer and binding sites all overlap indiscriminately, a maximally fit recognizer evolves in a tiny population within a small number of generations.
Despite numerous attempts, Intelligent Design Creationists haven’t been able to refute any of Dr. Schneider’s claims or the evidence provided by ev. His history of responses to creationists is both amusing and devastating to his critics.
Unlike his IDCist critics, Schneider uses a clear, unambiguous, measurable definition of information and demonstrates that even the simplest known evolutionary mechanisms can increase it. Shannon information is produced randomly in the context of the environment but is preserved non-randomly by selection. Differential reproductive success does, therefore, generate information. As Schneider succinctly puts it:
Replication, mutation and selection are necessary and sufficient for information gain to occur.
This process is called evolution.
— Thomas D. Schneider
Please contact me by email if you have any questions, comments, or suggestions.

Patrick:
You can simply inspect the code, either mine or Dr. Schneider’s, to see that the only changes to the genomes from one population to the next are random. Information is generated randomly but preserved non-randomly, just as in biological evolution.
If you turn off “selection,” all the information is lost. If you never turn it on, no information arises. Everything hinges on what “selection” does. What does it do? It eliminates half of a “population” with the worst ‘weight’ values. The effect of this is to slow down the changes that take place in the binding sites. After a few generations and its subsequent ‘eliminations’ (“selection”), the binding sites almost hardly change at all. The “threshold” hardly changes. So it’s just a matter of time for the sites to align via the weight matrix.
When you turn off “selection,” then the program is truly ‘random,’ but, then, nothing happens. Why not turn off the “weight” matrix: just have the binding sites and donor sites ‘evolve’ randomly? But, of course, we all know that nothing would happen.
All of this has been handled by Dembski and Marks and Ewert. Again, I’ll leave it to them.
PaV: (1) The most obvious is the mutation rate. Schneider compares the ev mutation rate to the HIV-1 virus, and notes that it is ten times faster!
. . . The human genome mutation rate is more than 10,000 times slower. Should we just ignore this?
Patrick:
Both the ev genome and the population size are extremely small compared to biological genomes and populations. It’s not surprising that a higher mutation rate is required to observe evolution within a reasonable number of CPU cycles. That doesn’t mean that less efficient settings won’t work.
I’m not talking about “efficiency,” I’m talking about how the ev program does NOT reflect how nature works. You’ve made my point.
PaV:
(2) Immediately after saying his model “matches” biology, in the very next sentence he writes: “Because half of the population always survives each selection round in the evolutionary simulation presented here, the population cannot die out, and, there is no lethal level of incompetence. While this may not be representative of all biological systems, since extinctions and threshold effects do occur, it is representative of the situation in which a functional species can survive without a particular genetic control system but which would do better to gain control ab initio.
This almost contradicts him.
Patrick:
There is no contradiction in what you quoted. He’s merely pointing out where ev models biology and where it does not.
Schneider’s use of truncation selection is also not an issue. I was able to reproduce his results using tournament selection, with a variety of tournament pool sizes and mutation rates.
Let’s stick to ev. Did I say he “contradicted” himself, or did I say he “almost contradicts” himself?
PaV:
But the distinction that he sees as ‘saving’ him, actually undermines his program.
That is:
(3) Schneider invokes “gene duplication”. . . . Schneider doesn’t expound here on his point, but he is basically saying that via gene duplication, and because of the presence of cell machinery that is simply a given for each cell/organism, and because of the nature (and location–which he doesn’t speak much about, but does have relevance here, though I’m not going to address that) of the incipient binding site on the RNA/DNA, this “process of evolution of new binding sites” falls outside of ‘purifying selection.’ IOW, as he states, the organism/cell doesn’t need this ‘control’; it will simply operate ‘better’ with it. So, this ‘process’ is effectively invisible to natural selection.
Patrick:
Now here is a contradiction, in your final sentence. Schneider points out that one known evolutionary mechanism that results in new functionality is gene duplication followed by mutation. He notes, in the excerpt you provided, that while an organism does not need the new functionality (if it did it wouldn’t be viable), it operates better with it.
Operating better is a selectable feature. Your claim that it is “invisible to natural selection” does not follow from what Schneider wrote.
There is no contradiction in what I wrote. You’ve missed the point.
The point, and it should be obvious, is that the “binding sites” are of NO value until they actually “function” as a binding site!
Yes, when the new “control” in in place, hypothetically, i.e., for the sake of argument, this is “better” for the organism; but it is NOT better as the sequence which will BECOME the “binding site” is ‘mutating’ itself there.
PaV:
But, wait a second, we have a problem here:
(4) Schneider himself tells us that if switches off “selection,” then the information gains disappear!! So, he is invoking a process that is invisible to “selection,” but then his notion of “selection” (which, again, is of its own problematic) becomes critical for the information to arise (as my own runs on his ev program have aptly demonstrated), and to remain.
This is a serious problem.
Patrick:
It’s not a problem at all. Improvements to function within a particular environment are selectable.
You can’t “select” what doesn’t exist yet.
PaV:
But the problem has a deeper basis:
(5) Schneider uses a “weight” matrix in his model. After each run, all of the binding sites are evaluated algebraically using this matrix and then assigned a value. Then the value of these sites is added up [and] given, if you will, a total score for that particular genome.
Here’s the even more serious problem(s). First, the “score” can only be arrived at by knowing what the target sequence is. This is almost exactly like Dawkin’s “Me Think It Is A Weasel” example where arriving at the target sequence completely randomly is near impossible, but can be reached somewhat easily if every “correct” character is kept. The obvious difference here is ONLY that the “target sequence” can change—though it won’t change rapidly.
Patrick:
You misunderstand the implementation of ev. The weight matrix, the threshold for recognizing a binding site, and the multiple (sixteen by default) binding sites are all part of the genome and all are subject to mutation. Using Schneider’s default settings, there are 256 (sic) potential binding sites of width 6 yielding a genome length of 261. The weight matrix consists of 24 integers encoded by 5 bases each for a total of 120 bases. The threshold consists of another 5 bases. That means that almost 48% of the genome encodes the recognition mechanism.
The number of bases used to encode binding sites is 96. Plus, these binding sites overlap with the recognizer and with each other. Some mutations may impact the recognizer and three binding sites.
Given that, it’s obvious that your claim that the “target sequence” (which doesn’t exist in ev) “won’t change rapidly” is false. It will change nearly half the time a mutation takes place.
The “won’t change rapidly” statement refers to how the program actually works. If you observe the population across generations, you’ll find that because of “selection” there’s a kind of homogeneity of the overall population that is maintained. It is random at first, but quickly becomes non-random. But, of course, if you turn off “selection” it will continue to be ‘random’ forever.
So the fact that “selection” cannot take place until an actual binding site is arrived at makes the use of “selection” from the get-go inappropriate. But, of course, if “selection” isn’t turned on from the get-go, you get nothing.
PaV:
For example, if one can “find” the correct binding sites on average in 750 generations or so, and, if there is only ONE mutation per generations, this means the binding sites don’t quickly make dramatic changes, an effect that is incredibly heightened by Schneider’s decision to “eliminate” half of the genomes in each generation, which in short order introduces an almost constant set of binding sites.
Patrick:
As already noted, the specific selection mechanism is immaterial. Evolution still occurs.
The binding sites are also not “almost constant”. The whole point of using a weight matrix is to model the biological fact that binding sites do not consist of a set sequence of nucleotides. If you run Schneider’s Java implementation you will see the range of bases in each binding site.
For one binding site, 16 bases long, on average there will be 16/261, or roughly, one change in every 16 generations. That’s not a lot. When you’re duplicating half of the binding sites each generation, that’s a great big movement toward homogeneity.
PaV:
Patrick writes above that when he increased the mutation rate for the program it took “longer” to optimize the binding sites: in real life we would expect the opposite for a randomly produced effect.
Patrick:
That doesn’t follow. In both biological and software evolution there are mutation rates that are too high to result in viable populations. Consider the impact of high radiation levels, for just one biological example.
If the Darwinian model is based on NS+RM, the more things mutate, then the faster something should evolve. Now, the fact that lots of mutation leads to death ought to make one question the model, right?
PaV:
All this means:
(6) The way the ev program works is by having “selection” able to see not just random processes that produce no fitness effects, but, even more increduously, “selection” can “see” the steps on the way to a fitness effect. That’s what the “weight” matrix does: it takes each step of the way, evaluates it, selects for it, eliminates all the bad genomes, and then moves on.
Patrick:
As noted above, your claim that the random processes in ev “produce no fitness effects” is incorrect. The rest of your paragraph depends on that faulty assumption.
Turn off “selection,” and then wait for a binding site to develop. Then “select” for that binding site. Nothing will happen this way.
PaV:
It is no small wonder, then, that “new information” is produced. But this is not what happens in nature. It is simply not a realistic model of life.
Patrick:
Differential reproductive success based on heritable characteristics is exactly what we observe in life.
Yes. We call this “microevolution,” and almost everyone in the ID community accepts this.
But you have a “fitness function” telling you about the fitness of a “binding site” even before the “binding site” has function. This doesn’t happen in real life.
PaV:
Unlike Dawkins’s simulation, Schneider’s does not identify an explicitly given target sequence. Even so, it identifies target sequences implicitly through the choice of fitness function. Moreover, by tying fitness to number of mistakes, Schneider guarantees that the gradients of his fitness function rise gradually and thus that his evolutionary algorithm converges in short order to an optimal computational sequence (optimality being defined in relation to his fitness function). Although once the algorithm starts running there is no intervention on the part of the investigator, it is not the case that Schneider didn’t intervene crucially in structuring the fitness function. He did, and this is where he smuggled in the complex specified information that he claimed to obtain from scratch.
(My bolding)
Patrick:
The fitness function is analogous to the environment in biological evolution. If that “smuggles in” information, then so does the environment.
Dembski appears to be complaining that ev models biological evolution and demonstrates that simple, known evolutionary mechanisms result in measurable information gain. I can see how that’s a problem for Dembski’s religious beleifs, but it’s hardly an argument against what ev demonstrates.
No, ev is not a problem for Dembski’s “religious beliefs,” but, rather, for his intellect. No one likes to have their intellect insulted.
Patrick:
To summarize:
1) The mutation rate discussion is a red herring.
2) The selection method used does not change the results.
3) The improvements provided by binding sites model selectable functionality in biological organisms.
4) There is no target sequence.
5) The recognizer does mutate as much as the rest of the genome.
6) Binding sites are not “almost constant”.
As to (1), the mutation rate only serves to point out how unlike nature the ev program is.
As to (2), you couldn’t be more wrong. Everything hinges on how “selection” is constituted in the program.
As to (3), this isn’t true when the binding sites are not “functional.” They’re being guided via the weight matrix to the proper configuration, and then kept. Selection should work for the second part, but not the first.
As to (4), there is no “static” target sequence; however, via “selection,” “threshold”, and weight matrices, while these change slowly with each generation, they constitute a mathematical whole which never loses sight of each. Yet, despite this mathematical advantage, nothing happens unless one half of the genome is copied each generation. This has the effect of making the mathematical system a somewhat “static” system; then it’s just a matter of time before the proper equations are arrived at.
As to (5), yes, the recognizer portion changes also. And nothing would happen unless half of the populations is removed, including the recognizer portion, each generation. You know, you don’t want it to be too random.
As to (6), let me restate: they change slowly.
Patrick:
Intelligent design creationists should really write some code and run some tests before making assertions.
I’ve run the ev program. Many times. The problem is not “reading code,” but importing information via fitness functions as Dembski states above. Added to that, the “selection” being used is completely artificial, and it has the effect of eliminating large distances between the recognizer portion and the binding site portion. These are the gulfs of improbability that ID points to. ev simply eliminates it via non-random fitness functions via the “selection” protocol.
[[N.B. I have no idea what happened here with the formatting. It is formatted perfectly in my word file. Sorry for the difficulties this represents. I’ve tried to correct it, but have no idea what is preventing me from doing so.]]
Mung,
It would really help if you ID supporters would acknowledge the following:
1. The closest thing to a “search” in evolution (and ev) is the generation of variants with subsequent shifts in their prevalence due to their differential reproductive success. No intelligent being is doing the “searching”.
2. The closest thing to a “target” is “anything at all having better fitness”. The “target” is not some specific protein or a particular adaptation such as the bacterial flagellum.
3. The only sense in which the process is “directed” is that the fitness function favors some variants over others. No intelligent being is doing the “directing”.
There is no support for ID in any of the above. So why the desperate push to get ID critics to use the words “search”, “target”, and “directed”?
Is that really the best you’ve got, Mung?
When there is no convergence to a solution I’ll believe there’s no target.
Do you think that targets cannot move? Do you think that because targets are created at runtime and may differ across various runs of the program that it follows that there is are no targets?
Is that a rhetorical question?
I’ve asked you this a million times. How do you know when a GA, especially one that implements drift, has reached or converged into a solution?
keiths:
Mung:
No, I’m really asking. If you have something better, now would be the time to produce it. Your equivocation strategy is going nowhere.
If you don’t have anything better, now would be the time to give up.
The way that I recall things I was the one asking that question.
You have to be kidding me. There’s no target, so there’s no way to answer that. It was your question so there’s your answer, there’s no target
I might be confused, but isn’t that question-begging? Are you requiring in advance that the test fail?
Do you think that biological evolution has a target?
I’m trying to understand what you, and possibly other IDCists, mean by “target”. Unlike Dawkins’ Weasel, most GAs, including ev, don’t have an explicit solution in mind. There is no way to tell with ev what the recognizer and binding sites will look like, and they are different from one run to the next. They’re even different among genomes in a population during much of the run.
Is “co-evolve a recognizer and a set of binding sites” a target? That’s all the fitness function rewards in ev.
It appears to have many targets.
Of course. If you start out with the WEASEL phrase and occasionally change one of the letters it does not therefore cease to be a target. When a == b return solution. That’s a search with a target.
Your equivocation strategy is going great guns.
So? What does this have to do with anything?
When you use a sort (qsort function) in your WEASEL program is it your contention that in that case it is an intelligent being doing the sorting?
And yet those things allegedly exist just because they provided better fitness. IOW, they were “targets.” It seems odd to us that better fitness can be a target but those things that are the cause of better fitness cannot be a target. Explain your logic for making that distinction.
You’re doing a fantastic job of equivocating. Even you don’t seem clear on what you’re talking about it. What fitness function?
I can write a function that can be used to compare objects and rank them as less than greater than or equal. Like a fitness function. I can then use that to sort the objects, after which they will be ordered and have a clear directionality. All without an intelligent being doing the directing. Amazing, really.
doubt it.
Without differential reproductive success based on heritable traits evolution does not occur in either biological or software systems. So?
That’s the truncation selection mechanism used by Dr. Schneider. I used other mechanisms as well, including tournament selection with varying tournament sizes. Evolution still occurred. Your focus on truncation is another red herring.
Wrong. The mutation rate is independent of the selection mechanism.
The selection mechanism tends to (those I used are stochastic) result in the more fit genomes leaving more descendents in subsequent populations. Just as with biological evolution.
That’s not accurate. They change at the same rate throughout the run. Those that are more fit within the environment simply reproduce more than those that are less fit.
The threshold changes at the same rate as any other similarly sized portion of the genome. You really should examine the code and run some tests before making claims like this.
Of course not. Why would you expect it to? Without differential reproductive success based on heritable traits you don’t observe evolution.
But when we do have differential reproductive success based on heritable traits, we observe evolution, both in biological and software systems.
You seem very confused about what evolution actually is and what ev demonstrates. You also seem to be confusing what happens to individual genomes with what happens to the population as a whole. Populations evolve, individual genomes do not. What exactly is your point with all this discussion of selection?
The rest of your comment seems to depend on this confusion, so I’ll defer responding for now.
Patrick:
Without differential reproductive success based on heritable traits evolution does not occur in either biological or software systems. So?
Your favorite term seems to be “red herring.” Well, this is a “red herring.” There’s two problems: (1) the extreme amount of “selection” that takes place each generation; and, (2) the way in which “organisms” are “selected.” This is where the fitness function comes in.
Speaking of which . . .
PaV:
Everything hinges on what “selection” does. What does it do? It eliminates half of a “population” with the worst ‘weight’ values.
Patrick:
That’s the truncation selection mechanism used by Dr. Schneider. I used other mechanisms as well, including tournament selection with varying tournament sizes. Evolution still occurred. Your focus on truncation is another red herring.
Well, instead of asking us to now analyze your GA and find its flaws, let’s stick to the ev program.
Answer this question: did your program work the first time all the errors were out, or did you have to “fine-tune” it to get the desired result?
PaV:
The effect of this is to slow down the changes that take place in the binding sites.
Patrick:
Wrong. The mutation rate is independent of the selection mechanism.
You should think through what I said a little bit more. When half of the population is duplicated each generation, you’ve got a lot of stuff that is similar, and with the same mutation rate applying, the similarity begins to add up; and this, of course, “slow[s] down” the rate at which the changes are taking place.
PaV:
After a few generations and its subsequent ‘eliminations’ (“selection”), the binding sites almost hardly change at all.
Patrick:
That’s not accurate. They change at the same rate throughout the run. Those that are more fit within the environment simply reproduce more than those that are less fit.
But, as I’ve pointed out already, this enhanced “reproduction” takes place before there is any beneficial effect. IOW, even when the binding site is NOT binding, it’s being “selected” for. That’s not how evolution supposedly takes place in nature.
PaV:
The “threshold” hardly changes. So it’s just a matter of time for the sites to align via the weight matrix.
Patrick:
The threshold changes at the same rate as any other similarly sized portion of the genome. You really should examine the code and run some tests before making claims like this.
How many times are you going to say I should run some tests before making claims. I’ve told you more than once that I’ve run lots tests. That was years ago, but I still remember what I saw. And one of the things I saw was that the threshold value changed very, very slowly, hardly at all once a number of generations were behind you.
And, of course, this makes perfect sense. Why? Because this value is determined by the smallest number of bases! Hence the probability of it changing via mutation is the least.
PaV:
When you turn off “selection,” then the program is truly ‘random,’ but, then, nothing happens.
Patrick:
Of course not. Why would you expect it to? Without differential reproductive success based on heritable traits you don’t observe evolution.
But again, it’s not so much that “selection” is taking place, but how. See my first response above.
What ought to be done is to turn off “selection” until you have a binding site that is “functional.” Then “select” that one binding site, and keep the rest. Then you would mirroring what evolution is supposed to be like.
But something much more than this takes place in ev, which helps everything along, not just the organisms with a ‘selective’ advantage.
PaV:
Why not turn off the “weight” matrix: just have the binding sites and donor sites ‘evolve’ randomly? But, of course, we all know that nothing would happen.
Patrick:
But when we do have differential reproductive success based on heritable traits, we observe evolution, both in biological and software systems.
When the program first starts up, in the first generation, there are NO binding sites, or perhaps one, simply by chance. But what is “selected” are the binding sites that, per the weight matrix and threshold, have the highest values. What, exactly, is this “selection” based on?
Patrick:
You seem very confused about what evolution actually is and what ev demonstrates.
This is just patronizing pap. Oh, gee, let me think hard. What does evolution consists of? Oh, yeah, I remember, random mutation and natural selection. Is this supposed to be hard.
It’s not I who am confused; rather, it is you who are choosing to ignore the ways in which ev does not reflect what evolution is thought to be like. When there are two binding sites, or three, or four—all the way up to seven—you have ‘binding sites’ being ‘selected’ for that aren’t functional. If you can’t see that this isn’t how evolution is purported to work, then it would seem it is you who are confused.
Patrick:
You also seem to be confusing what happens to individual genomes with what happens to the population as a whole. Populations evolve, individual genomes do not. What exactly is your point with all this discussion of selection?
Selection applies only to those organisms in a population that have some beneficial adaptation. In ev, selection takes place indiscriminately. Organisms are being selected simply on the basis that they’re further along the route to being beneficial than others. This isn’t the “blind watchmaker,” but evolution with an eye to what is to come.
Now this might make you able to achieve an “optimal” solution, but it is not a real simulation of how natural selection purportedly operates. [N.B. I don’t necessarily mean to imply that NS doesn’t exist or take place, what I am implying, however, is that when what happens in organisms is properly understood, science will no longer call this process NS.]
I hope by using the term “find” you don’t mean to imply that there is any sort of “search” going on.
Can you explain how, other than just performing a calculation, the figure of 7.64 bits is arrived at? Feel free to use a simpler example. Let me explain what i mean.
If we have 8 boxes and a coin in one of those 8 boxes it would take three bits of information to find the coin. We’re assuming that the likelihood of the coin being in a particular one of the 8 is equally probable. Assuming “maximum entropy.” For convenience let’s number the boxes 1-8.
So we ask is the coin in box 1-4? No.
Is the coin in box 5 or 6? No.
Is the coin in box 7? No.
Therefore the coin is in box 8.
So we’re talking about the number of yes/no questions.
Is that the same mechanism more or less used to arrive at the figure of 7.64 bits of information on average to find one of the 5 binding sites?
Question about the list of required files.
The required files are:
ga-ev-package.lisp
ga-ev.lisp
examples/ga-ev-package.lisp
examples/ga-ev.lisp
examples/load-ev.lisp
This makes it appear as if two required files exist in the parent directory to the examples directory. There are no “-ev’ files in the parent directory. Are five files required, the three files in the examples directory and two files in the parent directory?
ga-package.lisp
ga.lisp
Update your README and I wouldn’t have to ask. 😉
ETA: NM. Found it.
(load (compile-file “../ga-package.lisp”))
(load (compile-file “../ga.lisp”))
(load (compile-file “ga-ev-package.lisp”))
(load (compile-file “ga-ev.lisp”))
That’s a reasonable analogy, yes. Basically, the calculation yields how many bits it takes to identify
yields how many bits it takes to identify  locations in a string of length
locations in a string of length  .
.
Yup, the file names were wrong. I’ve updated the post. Thanks!
ok, so let’s approach from a slightly different angle.
We ask is the coin in box 1? No.
Is the coin in box 2? No.
Is the coin in box 3? No.
Is the coin in box 4? No.
Is the coin in box 5? No.
Is the coin in box 6? No.
Is the coin in box 7? No.
Therefore the coin is in box 8.
That requires seven bits of information rather than 3. That’s a pretty significant difference. How do you account for the difference?
ETA: now imagine if it were 200 boxes rather than 8.
3 bits would obviously be the minimum
I’ve got a better one for you. Put all the boxes in a bigger box. Shake it up. Pull out one box. If the coin isn’t in the box, put it back in the bigger box. Shake it again.
As dazz already pointed out, the formula for calculates the minimum amount of information required to identify a site.
calculates the minimum amount of information required to identify a site.
One of the interesting results of ev is that could be much larger, but it always oscillates around
could be much larger, but it always oscillates around  .
.
Obviously. How did the ev program manage to just happen to hit upon the minimum? Blind luck?
Like this?
number_of_slots = 8
iterations = 1_000_000
guesses = 1
iterations.times do
# create an array with the given number of slots
boxes = Array.new(number_of_slots)
# randomly populate 1 of the slots
boxes[rand(number_of_slots)] = true
# try to guess the slot until successful
# no memory of past attempts
loop do
break if boxes[rand(number_of_slots)] == true
guesses += 1
end
end
puts guesses
puts guesses / iterations
ETA: For grins, change number_of_slots to 200.
Are you being deliberately stupid or what?
Are you taking the cowards way out or what?
Evolution.
I nicked the idea from bogosort. There is some example code linked from that page.
Was the question too taxing? Did you not understand it? Do you need to call a friend? I bet keiths would know. Maybe DNA_Jock will chime in with something about partitioned search.
There is nothing in the ev implementation that requires that R_{sequence} evolve to R_{frequency}, yet it does every time.
You may as well express amazement that the program manages to employ the optimal search strategy, every time. Praise Evolution!
I’d question the premise that there’s nothing in the ev program requiring it to use the optimum search strategy.
I answered your question. If you find that answer unsatisfying somehow, please ask any additional questions you need to clarify your understanding.
What makes you think either my or Dr. Schneider’s programs “employ the optimal search strategy”? What do you think the optimal search strategy is?
The code is available. Please point to where it ensures that evolves to and oscillates around
evolves to and oscillates around  . Don’t you find it interesting that, using only simple evolutionary mechanisms, ev demonstrates the same behavior that is observed in nature?
. Don’t you find it interesting that, using only simple evolutionary mechanisms, ev demonstrates the same behavior that is observed in nature?
I give you credit for at least looking at that particular measure. None of the intelligent design creationist luminaries or water boys have done so yet.
Thank you.
The one that maximizes the amount of information obtained per yes/no query. [This is what I was trying to convey with my examples. dazz caught on but then punted.] Do you have a better answer than the one I have just given? Do you agree that for my example this is three bits?
I find it remarkable that the ev program appears to be using a search strategy that is optimal. Do you think it can do better?
Yes, you’ve already convinced me that lisp is loathsome. 🙂
And the Java version has presentation code mixed in to the logic. Yech.
The Pascal code is on an old PC.
Have you done the math to find out if a different information measure would alter the results? Just asking, I haven’t, but I’m willing to bet it wouldn’t
And of course it’s in Shannon’s paper itself:
Mung, did you happen to notice when, in the Weasel thread, a fitness function conversion could be done to use a selective coefficient that goes in the range of [0, 1) from Prof. Felsenstein’s definition of a selective coefficient that was defined in the [0, infinity) range?
Looks to me like the same case here (that’s when you complained that selective coefficients were supposed to go [0, 1))
I concur.
Read Seibel’s book. Come to the light side.
The fact that the information in the binding sites evolves to oscillate around the minimal information required to identify a site in the genome doesn’t mean that the mechanism by which that evolution occurred is an “optimal search strategy.” In fact, evolutionary mechanisms are profligate. Hundreds of thousands of genomes die to reach that point.
You’re confusing the mechanism with the result.
Patrick,
The information evolves by design
Seems to me it’s even worse than that. He somehow seems to suggest that the choice of bits to measure information (base 2 log) implies some sort of optimization of the process. Sounds like the good old “you smuggled the optimization” trope
Patrick, for you have this formula
you have this formula 
Patrick,
But then you make the calculation in your example for
Unless I’m missing something here it should be … 5.32 bits
… 5.32 bits
And you are jumping to a conclusion that is not warranted by the available evidence. You’ve once again failed to accurately read my mind.
I am looking at the result and asking why that result and not some other result. I’ve posted an algorithm that gives a completely different result. So far the best explanation you’ve given for the difference is “evolution.”
Do you agree that the strategy I presented which arrives at the answer in three yes/no questions is the optimal strategy? Do you agree that we can expand the number of boxes and use the same strategy with the same results? Can you find a strategy that does better than the one I gave?
If not, why is it unreasonable to infer that ev must be using a similar strategy since it produces a similar result?
If you don’t have time to really think about this I am fine with that. I understand about the demands life makes. But please don’t be dismissive. Don’t you find the question at least somewhat interesting?
Yours was no strategy, just a reformulation of how to measure information. Instead of bits to represent N “boxes” ( ) your measure would yield a value of
) your measure would yield a value of  for information. If you replace every logarithmic measure in those formulas with yours, I’m pretty sure the algo would converge all the same.
for information. If you replace every logarithmic measure in those formulas with yours, I’m pretty sure the algo would converge all the same.
Sure it was. All you have to do is think of it as a betting game in which you have to pay for each guess you make and either maximize your winnings or minimize your losses and it’s nature as a strategy becomes obvious.
Don’t deny the obvious.
What does any of that have to do with ev, the topic at hand? Do you agree that your “strategy” only modifies the way information is quantified? It’s sort of funny that you would attack ev for it’s supposed optimization while DEM did the opposite, complain about it’s inefficiency
I see how my explanation was sloppy. Since is 1000, it should be
is 1000, it should be  which is approximately 7.64. Sorry for the confusion.
which is approximately 7.64. Sorry for the confusion.