Recent discussions of genetic algorithms here and Dave Thomas’ evisceration of Winston Ewert’s review of several genetic algorithms at The Panda’s Thumb prompted me to dust off my notes and ev implementation.
Introduction
In the spring of 1984, Thomas Schneider submitted his Ph.D thesis demonstrating that the information content of DNA binding sites closely approximates the information required to identify the sites in the genome. In the week between submitting his thesis and defending it, he wrote a software simulation to confirm that the behavior he observed in biological organisms could arise from a subset of known evolutionary mechanisms. Specifically, starting from a completely random population, he used only point mutations and simple fitness-based selection to create the next generation.
The function of ev is to explain and model an observation about natural systems.
— Thomas D. Schneider
Even with this grossly simplified version of evolution, Schneider’s simulator, tersely named ev, demonstrated that the information content of a DNA binding site, ![]() , consistently and relatively quickly evolves to be approximately equal to the information required to identify the binding sites in a given genome,
, consistently and relatively quickly evolves to be approximately equal to the information required to identify the binding sites in a given genome, ![]() , just as is seen in the biological systems that were the subject of his thesis.
, just as is seen in the biological systems that were the subject of his thesis.
Schneider didn’t publish the details of ev until 2000, in response to creationist claims that evolution is incapable of generating information.
Core Concepts
Before discussing the implementation, it’s important to understand exactly what is being simulated. Dr. Schneider’s thesis is quite readable. The core concepts of ev are binding sites, ![]() , and
, and ![]() .
.
Binding Sites
A binding site is a location on a strand of DNA or RNA where a protein can attach (bind). Binding sites consist of a sequence of nucleotides that together provide the necessary chemical bonds to hold the protein.
A good example of binding sites in action is the synthesis of messenger RNA (mRNA) by RNA polymerase (RNAP). RNAP binds to a set of a few tens of base pairs on a DNA strand which triggers a series of chemical reactions that result in mRNA. This mRNA is then picked up by a ribosome (which also attaches to a binding site) that transcribes a protein from it.
The bases that make up a binding site are best described by a probability distribution, they are not a fixed set requiring an exact match.
![]() is the simplest of the two information measures in ev. Basically, it is the number of bits required to find one binding site out of set of binding sites in a genome of a certain length. For a genome of length
is the simplest of the two information measures in ev. Basically, it is the number of bits required to find one binding site out of set of binding sites in a genome of a certain length. For a genome of length ![]() with
with ![]() binding sites, this is
binding sites, this is ![]()
For example, consider a genome of 1000 base pairs containing 5 binding sites. The average distance between binding sites is 200 bases, so the information needed to find them is ![]() which is approximately 7.64 bits.
which is approximately 7.64 bits.
![]() is the amount of information in the binding site itself. There are two problems with computing
is the amount of information in the binding site itself. There are two problems with computing ![]() . The first is the definition of “information.” Schneider uses Shannon information, a clearly defined, well-respected metric with demonstrated utility in the study of biological systems.
. The first is the definition of “information.” Schneider uses Shannon information, a clearly defined, well-respected metric with demonstrated utility in the study of biological systems.
The second problem is that binding sites for the same protein don’t consist of exactly the same sequence of bases. Aligned sequences are frequently used to identify the bases that are most common at each location in the binding site, but they don’t tell the whole story. An aligned sequence that shows an A in the first position may reflect a set of actual sites of which 70% have A in the first position, 25% C, and 5% G. ![]() must take into account this distribution.
must take into account this distribution.
The Shannon uncertainty of a base in a binding site is:
(1) 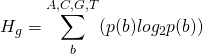
where ![]() is the probability of a base
is the probability of a base ![]() at that location in the genome. This will be approximately 0.25, equal probability for all bases, for the initial, randomly generated genome. The initial uncertainty at a binding site is therefore:
at that location in the genome. This will be approximately 0.25, equal probability for all bases, for the initial, randomly generated genome. The initial uncertainty at a binding site is therefore:
(2) ![]()
where ![]() is the width of the site.
is the width of the site.
![]() , the increase in information, is then
, the increase in information, is then ![]() , where:
, where:
(3) 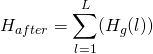
computed from the observed probabilities.
There is one additional complexity with these formulas. Because of the small sample size, an adjustment must be computed for ![]() :
:
(4) 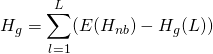
or
(5) 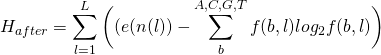
measured in bits per site.
The math behind the small sample adjustment is explained in Appendix 1 of Schneider’s thesis. Approximate values for ![]() for binding site widths from 1 to 50 are available pre-computed by a program available on Schneider’s site:
for binding site widths from 1 to 50 are available pre-computed by a program available on Schneider’s site:
For a random sequence, ![]() will be near 0. This will evolve to
will be near 0. This will evolve to ![]() over an ev run.
over an ev run.
Schneider’s ev Implementation
Schneider’s implementation is a fairly standard genetic algorithm, with an interesting fitness function. The virtual genomes contain, by default, 256 potential binding sites. The genomes are composed of characters from an alphabet of four letters (A, C, G, and T). The default number of optimal binding sites, ![]() , is 16. The locations of these sites are randomly generated at the beginning of each run and remain the same throughout the run. Given this configuration,
, is 16. The locations of these sites are randomly generated at the beginning of each run and remain the same throughout the run. Given this configuration, ![]() , the amount of information required to identify one of these sites in a genome of length
, the amount of information required to identify one of these sites in a genome of length ![]() is
is ![]() which equals 4. Per Schneider’s Ph.D thesis,
which equals 4. Per Schneider’s Ph.D thesis, ![]() , the information in the binding site itself, should evolve to and remain at approximately this value during a run.
, the information in the binding site itself, should evolve to and remain at approximately this value during a run.
To determine the number of binding sites actually present, a portion of the genome codes for a recognizer as well as being part of the set of potential binding sites. This recognizer, which is subject to the same mutation and selection as the rest of the genome, is applied at each base to determine if that base is the start of a binding site. If a base is not correctly identified as the start of a binding site, the fitness of the genome is decreased by one. If a base is incorrectly identified as the start of a binding site, the fitness of the genome is also decreased by one. Schneider notes that changing this weighting may affect the rate at which ![]() converges to
converges to ![]() but not the final result.
but not the final result.
After all genomes are evaluated, the half with the lowest fitness are eliminated and the remaining are duplicated with mutation. Schneider uses a relatively small population size of 64.
The recognizer is encoded as a weight matrix of ![]() two’s-complement integers, where
two’s-complement integers, where ![]() is the length of a binding site (6 by default). Schneider notes that:
is the length of a binding site (6 by default). Schneider notes that:
At first it may seem that this is insufficient to simulate the complex processes of transcription, translation, protein folding and DNA sequence recognition found in cells. However the success of the simulation, as shown below, demonstrates that the form of the genetic apparatus does not affect the computed information measures. For information theorists and physicists this emergent mesoscopic property will come as no surprise because information theory is extremely general and does not depend on the physical mechanism. It applies equally well to telephone conversations, telegraph signals, music and molecular biology.
Since ev genomes consist only of A, C, G, and T, these need to be translated to integers for the weight matrix. Schneider uses the straightforward mapping of (A, C, G, T) to (00, 01, 10, 11). The default number of bases for each integer is ![]() . Given these settings, AAAAA encodes the value 0, AAAAC encodes 1, and TTTTT encodes -1 (by two’s-complement rules).
. Given these settings, AAAAA encodes the value 0, AAAAC encodes 1, and TTTTT encodes -1 (by two’s-complement rules).
When evaluating a genome, the first ![]() bases are read into the
bases are read into the ![]() weight matrix. The next
weight matrix. The next ![]() bases represent a threshold value that is used to determine whether or not the value returned by the recognizer is a binding site match. This is also a two’s-complement integer with the same mapping. The recognizer is then applied from the first base in the genome to the last that could possibly be the start of a binding site (given the binding site length).
bases represent a threshold value that is used to determine whether or not the value returned by the recognizer is a binding site match. This is also a two’s-complement integer with the same mapping. The recognizer is then applied from the first base in the genome to the last that could possibly be the start of a binding site (given the binding site length).
It’s worth re-emphasizing that the recognizer and the threshold are part of the genome containing the binding sites. The length of the full genome is therefore ![]() bases, with only the first
bases, with only the first ![]() bases being potential binding sites.
bases being potential binding sites.
The recognizer calculates a total value for the potential site starting at a given point by summing the values of the matching bases in the weight matrix. The weight matrix contains a value for each base at each position in the site, so for a binding site length of 7 and a potential binding site consisting of the bases GATTACA, the total value is:
w[0]['G'] + w[1]['A'] + w[2]['T'] + w[3]['T'] + w[4]['A'] + w[5]['C'] + w[6]['A']
If this value exceeds the threshold, the recognizer identifies the bases as a binding site.
This implementation of the recognizer is an interesting way of encapsulating the biological reality that binding sites don’t always consist of exactly the same sequence of bases. Schneider notes, though, that “the exact form of the recognition mechanism is immaterial because of the generality of information theory.”
Schneider’s Results
Using his default settings of:
- Genome length:
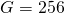
- Number of binding sites:
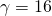
- Binding site length:
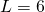
- Bases per integer:
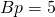
Schneider found that:
When the program starts, the genomes all contain random sequence, and the information content of the binding sites,
, is close to zero. Remarkably, the cyclic mutation and selection process leads to an organism that makes no mistakes in only 704 generations (Fig. 2a). Although the sites can contain a maximum of
bits, the information content of the binding sites rises during this time until it oscillates around the predicted information content,
bits . . . .
The Creationist Response
30 years after the original implantation and 16 years after it was published, Intelligent Design Creationists (IDCists) are still attempting to refute ev and are still getting it wrong.
Dembski In 2001
In 2001, William Dembski claimed that ev does not demonstrate an information increase and further claimed that Schneider “smuggled in” information via his rule for handling ties in fitness. Schneider reviewed and rebutted the first claim and tested Dembski’s second claim, conclusively demonstrating it to be false.
Schneider wryly addresses this in the ev FAQ:
Does the Special Rule smuggle information into the ev program?
This claim, by William Dembski, is answered in the on-line paper Effect of Ties on the evolution of Information by the ev program. Basically, changing the rule still gives an information gain, so Dembski’s prediction was wrong.
Has Dembski ever acknowledged this error?
Not to my knowledge.
Don’t scientists admit their errors?
Generally, yes, by publishing a retraction explaining what happened.
Montanez, Ewert, Dembski, and Marks In 2010
Montanez, Ewert, Dembski, and Marks published A Vivisection of the ev Computer Organism: Identifying Sources of Active Information in the IDCist’s pseudo-science journal BIO-Complexity in 2010. Despite its title, the paper doesn’t demonstrate any understanding of the ev algorithm or what it demonstrates:
- The authors spend a significant portion of the paper discussing the efficiency of the ev algorithm. This is a red herring — nature is profligate and no biologist, including Schneider, claims that evolutionary mechanisms are the most efficient way of achieving the results observed.
- Related to the efficiency misdirection, the authors suggest alternative algorithms that have no biological relevance instead of addressing the actual algorithm used by ev.
- The authors do not use Shannon information, instead substituting their idiosyncratic “active information”, including dependencies on Dembski’s concept of “Conservation of Information” which has been debunked by Wesley Elsberry and Jeffrey Shallit in Information Theory, Evolutionary Computation, and Dembski’s “Complex Specified Information”, among others.
- The authors note that “A common source of active information is a software oracle”. By recognizing that an oracle enables evolutionary mechanisms to work in software, they are admitting that those same mechanisms can explain what we observe in biological systems because the real world environment is just such an oracle. The environment provides information about what works and what doesn’t by ensuring that organisms less suited to it will tend to leave fewer descendants.
- The authors repeatedly claim that the “perceptron” used as a recognizer makes the ev algorithm more efficient. Their attempted explanation of why this is the case completely ignores the actual implementation of ev. They seem so caught up in Schneider’s description of the recognizer as a perceptron that they miss the fact that it’s nothing more than a weight matrix that models the biological reality that a binding site is not a fixed set of bases.
Basically the paper is a rehash of concepts the authors have discussed in previous papers combined with the hope that some of it will be applicable to ev. None of it is.
Schneider soundly refuted the paper in Dissection of “A Vivisection of the ev Computer Organism: Identifying Sources of Active Information”. He succinctly summarized the utter failure of the authors to address the most important feature of ev:
They do not compute the information in the binding sites. So they didn’t evaluate the relevant information (
) at all.
In a response to that refutation, Marks concedes that “Regardless, while we may have different preferred techniques for measuring information, we agree that the ev genome does in fact gain information.”
After that damning admission, Marks still doubles down on his spurious claim that the “Hamming oracle” makes ev more efficient:
Schneider addresses the hamming oracle issue by assuming that nature provides a correct fitness function (a hamming function) that allows for positive selection in the direction of our target. He argues that this fitness is based on a
biologically sensible criteria: having functional DNA binding sites and not having extra ones.
But this describes a target; this is the desired goal of the simulation. The fitness function actually being used is a distance to this target. This distance makes efficient information extraction possible.
That’s not a target. It provides no details about what a solution would look like or how to reduce the distance measured, it simply indicates how far away a genome is from being a solution. In fact, it does less than that because it doesn’t provide any information about the difference between an existing recognizer and an ideal recognizer. It also says nothing at all about the relationship between ![]() and
and ![]() .
.
Even as he tries to salvage the tatters of his paper, Marks makes another concession:
Reaching that point requires a particular shape to the fitness landscape to guide evolution.
He admits again that evolution does work in certain environments. The real world is one of those.
Nothing in Marks’ response changes the accuracy of Schneider’s summary in his refutation:
Aside from their propensity to veer away from the actual biological situation, the main flaw in this paper is the apparent misunderstanding of what ev is doing, namely what information is being measured and that there are two different measures. The authors only worked with
and ignored
. They apparently didn’t compute information from the sequences. But it is the increase of
that is of primary importance to understand. Thanks to Chris Adami, we clearly understand that information gained in genomes reflects ‘information’ in the environment. I put environmental ‘information’ in quotes because it is not clear that information is meaningful when entirely outside the context of a living organism. An organism interprets its surroundings and that ‘information’ guides the evolution of its genome.
Ewert in 2014
Winston Ewert published Digital Irreducible Complexity: A Survey of Irreducible Complexity in Computer Simulations in 2014, again in the IDCists’ house journal BIO-Complexity. This paper constituted 25% of the output of that august publication in that year. Ewert reviewed Avida, ev, Dave Thomas’ Steiner Trees, a geometric algorithm by Suzanne Sadedin, and Adrian Thompson’s Digital Ears, attempting to demonstrate that none of them generated irreducible complexity.
Michael Behe defined “irreducible complexity” in his 1996 book Darwin’s Black Box:
By irreducibly complex I mean a single system composed of several well-matched, interacting parts that contribute to the basic function, wherein the removal of any one of the parts causes the system to effectively cease functioning. An irreducibly complex system cannot be produced directly (that is, by continuously improving the initial function, which continues to work by the same mechanism) by slight, successive modifications of a precursor system, because any precursor to an irreducibly complex system that is missing a part is by definition nonfunctional.
Dave Thomas has shredded Ewert’s discussion of Steiner Trees, demonstrating that Ewert addressed a much simpler problem (spanning trees) instead.
Richard B. Hoppe has similarly destroyed Ewert’s claims about Avida.
Schneider does explicitly claim that ev demonstrates the evolution of irreducible complexity:
The ev model can also be used to succinctly address two other creationist arguments. First, the recognizer gene and its binding sites co-evolve, so they become dependent on each other and destructive mutations in either immediately lead to elimination of the organism. This situation fits Behe’s definition of ‘irreducible complexity’ exactly . . . .
Ewert quotes this claim and attempts to refute it with:
It appears that Schneider has misunderstood the definition of irreducible complexity. Elimination of the organism would appear to refer to being killed by the model’s analogue to natural selection. Given destructive mutations, an organism will perform less well than its competitors and “die.” However, this is not what irreducible complexity is referring to by “effectively ceasing to function.” It is true that in death, an organism certainly ceases to function. However, Behe’s requirement is that:
If one removes a part of a clearly defined, irreducibly complex system, the system itself immediately and necessarily ceases to function.
The system must cease to function purely by virtue of the missing part, not by virtue of selection.
It appears that Ewert is the one with the misunderstanding here. If there is a destructive mutation in the genes that code for the recognizer, none of the binding sites will be recognized and, in the biological systems that ev models, the protein will not bind and the resulting capability will not be provided. It will “immediately and necessarily” cease to function. This makes the system irreducibly complex by Behe’s definition.
Binding sites are somewhat less brittle, simply because there are more of them. However, if there is a destructive mutation in one or more of the binding sites, the organism with that mutation will be less fit than others in the same population. In a real biological system, the function provided by the protein binding will be degraded at best and eliminated at worst. The organism will have effectively ceased to function. It is this lack of function that results in the genome being removed from the gene pool in the next generation.
Given that the recognizer and binding sites form a set of “well-matched, interacting parts that contribute to the basic function” and that “the removal of any one of the parts causes the system to effectively cease functioning”, ev meets Behe’s definition of an irreducibly complex system.
The IDCist Discovery Institute touted Ewert’s paper as evidence of “an Excellent Decade for Intelligent Design” in the ten years following the Dover trial. That case, of course, is the one that showed conclusively that ID is simply another variant of creationism and a transparent attempt to violate the separation of church and state in the United States. If Ewert’s paper is among the top achievements of the IDC movement in the past ten years then it’s clear that reality-based observers still have no reason to take any IDCist pretensions to scientific credibility seriously. The political threat posed by intelligent design and other variants of creationism is, unfortunately, still a significant problem.
An Alternative ev Implementation
I have implemented a variant of Dr. Schneider’s ev in order to reproduce his results and explore the impact of some alternative approaches. My version of ev uses the GA Engine I wrote to solve Dave Thomas’ Steiner Network design challenge. This engine operates on bit strings rather than the characters used by Dr. Schneider’s implementation.
As described in the GA engine documentation, applying the GA engine to a problem consists of following a few simple steps:
- Create a class to represent the characteristics of the problem
The problem class
ev-problemcontains the parameters for genome length (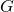 ), number of binding sites (
), number of binding sites (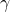 ), binding site length (
), binding site length (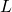 ), and bases per integer (
), and bases per integer (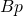 ).
). - Implement a method to create instances of the problem class
The
make-ev-problemfunction creates an instance ofev-problem. - Implement the required generic functions for the problem:
genome-length
The genome length is
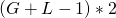 , using two bits to encode each base pair.
, using two bits to encode each base pair.fitness
The fitness of a genome is the number of mistakes made by the recognizer, the total of missed and spurious binding sites.
fitness-comparator
This problem uses the
greater-comparatorprovided by the GA engine. - Implement a
terminatorfunctionThis problem uses the
generation-terminatorprovided by the GA engine, stopping after a specified number of generations. - Run
solve
Initial Results
In my implementation, Schneider’s default settings and selection mechanism are configured like this:
(defparameter *default-ev-problem*
(make-ev-problem 256 16 6 5))
(let* ((problem *default-ev-problem*)
(gene-pool (solve problem 64 (generation-terminator 3000)
:selection-method :truncation-selection
:mutation-count 1
:mutate-parents t
:interim-result-writer #'ev-interim-result-writer))
(best-genome (most-fit-genome gene-pool (fitness-comparator problem))))
(format t "~%Best = ~F~%Average = ~F~%~%"
(fitness problem best-genome)
(average-fitness problem gene-pool)))This creates an instance of the ev-problem with 256 potential binding sites, 16 actual binding sites, a binding site width of 6 bases, and 5 bases per integer. It then evolves this population for 3000 generations using truncation selection (taking the top 50% of each gene pool to seed the next generation), changing one base in each genome, including the parent genomes, per generation.
The results are identical to those reported by Schneider. Over ten runs, each with a different random seed, the population evolves to have at least one member with no mistakes within 533 to 2324 generations (the mean was 1243.6 with a standard deviation of 570.91). ![]() approaches
approaches ![]() throughout this time. As maximally fit genomes take over the population,
throughout this time. As maximally fit genomes take over the population, ![]() oscillates around
oscillates around ![]() .
.
While my implementation lacks the GUI provided by Schneider’s Java version, the ![]() values output by
values output by ev-interim-result-writer show a similar distribution.
Variations
There are many configuration dimensions that can be explored with ev. I tested a few, including the effect of population size, selection method, mutation rate, and some problem-specific parameters.
Population Size
Increasing the population size from 64 to 256 but leaving the rest of the settings the same reduces the number of generations required to produce a maximally fit genome to between 251 and 2255 with a mean of 962.23 and a standard deviation of 792.11. A population size of 1000 results in a range of 293 to 2247 generations with a lower mean (779.4) and standard deviation (689.68), at a higher computation cost.
Selection Method
Schneider’s ev implementation uses truncation selection, using the top 50% of a population to seed the next generation. Using tournament selection with a population of 250, a tournament size of 50, and a mutation rate of 0.5% results in a maximally fit individual arising within 311 to 4561 generations (with a mean of 2529.9 and standard deviation of 1509.01). Increasing the population size to 500 gives a range of 262 to 4143 with a mean of 1441.2 and standard deviation of 1091.95.
Adding crossover to tournament selection with the other parameters remaining the same does not seem to significantly change the convergence rate.
Changing the tournament selection to mutate the parents as well as the children of the next generation does, however, have a significant impact. Using the same population size of 500 and mutation rate of 0.5% but mutating the parents results in a maximally fit individual within 114 to 1455 generations, with a mean of 534.1 and a standard deviation of 412.01.
Roulette wheel selection took much longer to converge, probably due to the fact that a large percentage of random genomes have identical fitness because no binding sites, real or spurious, are matched. This makes the areas of the wheel nearly equal for all genomes in a population.
Mutation Rate
In the original ev, exactly one base of 261 in each genome is modified per generation. This explores the fitness space immediately adjacent to the genome and is essentially simple hill climbing. This mutation rate is approximately 0.2% when applied to a string of bases represented by two bits each.
Changing the mutation count to a mutation rate of 1% results in ev taking an order of magnitude more generations to produce a maximally fit individual. Rates of 0.5% and 0.2% result in convergence periods closer to those seen with a single mutation per genome, both with truncation and tournament selection, particularly with larger population sizes. As Schneider notes, this is only about ten times the mutation rate of HIV-1 reverse transcriptase.
Binding Site Overlap
By default, binding sites are selected to be separated by at least the binding site width. When this restriction is removed, surprisingly the number of generations required to produce the first maximally fit genome ranges does not change significantly from the non-overlapping case.
Alternative Implementation Results
Population size seems to have the largest impact on the number of generations required to reach equilibrium. Mutation rate has a smaller effect, but can prevent convergence when set too high. Tournament selection takes a bit longer to converge than truncation selection, but the two are within the same order of magnitude. Roulette selection does not work well for this problem.
Unlike the Steiner network and some other problems, crossover doesn’t increase the convergence rate. Mutating the parent genomes before adding them to the next generation’s gene pool does have a measurable impact.
Regardless of selection method, mutation rate, or other parameters, ![]() always evolves to and then oscillates around
always evolves to and then oscillates around ![]() .
.
Source Code
The code is available on GitHub. The required files are:
ga-package.lispga.lispexamples/ga-ev-package.lispexamples/ga-ev.lispexamples/load-ev.lisp
To run from the command line, make the examples directory your working directory and then call
ccl64 - -load load-ev.lisp`
if you’re using Clozure CL or
sbcl - -load load-ev.lisp`
if you’re using Steel Bank Common Lisp.
If you need a refresher on Common Lisp programming, Peter Seibel’s Practical Common Lisp is an excellent book.
Summary
In addition to being a good test case for evolutionary algorithms, ev is interesting because of its biological relevance. As Schneider points out in his Results section:
Although the sites can contain a maximum of
bits, the information content of the binding sites rises during this time until it oscillates around the predicted information content
bits, with
bits during the 1000 to 2000 generation interval.
With this, ev sticks a spoke in the tires of creationists who complain that GAs like Richard Dawkins’ weasel program only demonstrate “directed evolution”. There is nothing in the ev implementation that requires that ![]() evolve to
evolve to ![]() , yet it does every time.
, yet it does every time.
It’s well worth running the Java version of ev to see the recognizer, threshold, and binding sites all co-evolving. This is a clear answer to creationist objections about how “irreducibly complex” parts could evolve.
The common creationist argument from incredulity based on the complexity of cell biochemistry is also touched on by ev. Even with a genome where the recognizer and binding sites all overlap indiscriminately, a maximally fit recognizer evolves in a tiny population within a small number of generations.
Despite numerous attempts, Intelligent Design Creationists haven’t been able to refute any of Dr. Schneider’s claims or the evidence provided by ev. His history of responses to creationists is both amusing and devastating to his critics.
Unlike his IDCist critics, Schneider uses a clear, unambiguous, measurable definition of information and demonstrates that even the simplest known evolutionary mechanisms can increase it. Shannon information is produced randomly in the context of the environment but is preserved non-randomly by selection. Differential reproductive success does, therefore, generate information. As Schneider succinctly puts it:
Replication, mutation and selection are necessary and sufficient for information gain to occur.
This process is called evolution.
— Thomas D. Schneider
Please contact me by email if you have any questions, comments, or suggestions.

Oops, yeah, that’s what I meant. Thanks for clarifying, just trying to get my head around all this one step at a time
I’m reading what you wrote.
You’ve shown that there are search mechanisms that are non-optimal. That’s well known. It also has nothing to do with what ev demonstrates.
I agree that your thought experiment shows how one could calculate the minimum information required to identify a site in a string.
If you mean your thought experiment could be expanded to have more than eight boxes and still arrive at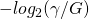 as the minimum information necessary to identify
as the minimum information necessary to identify 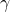 sites in a string of length
sites in a string of length 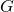 , sure.
, sure.
This is where your confusion apparently lies. Your box example is how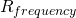 , not
, not 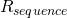 is calculated.
is calculated.
What’s interesting about ev is that the Shannon uncertainty of the binding sites (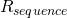 ) evolves to the information required to identify that many binding sites in a string of the length of the genome, using only a simple subset of known evolutionary mechanisms. Nothing in the code implements that.
) evolves to the information required to identify that many binding sites in a string of the length of the genome, using only a simple subset of known evolutionary mechanisms. Nothing in the code implements that.
So yes, it is unreasonable to infer that something like your box example is going on with respect to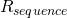 because you can look at the code and see that it is not.
because you can look at the code and see that it is not.
On the contrary, it simply seems to be one of your favorite logical fallacies.
Just to be clear, these are the two issues you have with ev? It’s a bit hard to tell what you point actually is.
I’m sure you’d prefer to ignore evidence that contradicts your claims. One of your two stated objections to ev is “the extreme amount of selection that takes place each generation.” I tested both the truncation selection used by Dr. Schneider and tournament selection with various tournament sizes (down to ten percent of the population), mutation rates, and other parameters like crossover and whether or not parents were mutated before being added to the next generation.
The results show that even without what you claim is “extreme selection”, the recognizer, threshold, and binding sites co-evolve and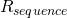 approaches and oscillates around
approaches and oscillates around 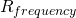 .
.
That’s an odd question. My first working version used the default parameters used in Dr. Schneider’s Java implementation. Once I eliminated any bugs in my code, it reproduced his results.
Why do you ask?
Let’s skip to your second issue, “the way in which organisms are selected.”
That isn’t even coherent. It smells a bit like the whole “latching” fiasco that took place at UD. It wouldn’t make any sense to preserve binding sites one at a time. That’s not how evolution works.
That is not correct. All that takes place in ev is random mutation plus differential reproductive success based on the co-evolving fitness function. When you watch a run, you’ll see the number of mistakes in the most fit genome slowly decrease over the generations. When a genome appears with one recognized binding site, it tends to reproduce more, but can be outcompeted by one that recognizes no binding sites but has fewer spurious hits.
This is analogous to biological evolution.
You have a fundamental misunderstanding of ev and selection. At the beginning of each run, the locations of the binding sites are randomly generated. In the first generation the number of mistakes in the most fit genome is usually around twenty, when using the default settings. This represents not recognizing any of the sixteen binding sites and recognizing a few locations that are not binding sites.
As the population evolves, the genomes with fewer mistakes have a higher probability of reproducing. Combined with random mutation, this eventually results in the average number of mistakes made by genomes in the population going down. Selection is based solely on the number of mistakes.
Not at all. ev models the biological reality that partial function gives a benefit in an environment where the rest of the population lacks that partial function.
I think you’ve got a long row to hoe before you can demonstrate that.
Thank you. It’s nice to know that I am capable of providing evidence in support of my claims.
Now can you kindly provide evidence in support of your claim that it is well known that there are search mechanisms that are non-optimal?
I don’t know whether to invoke Hitchens’ Razor here or to agree with you. What is it that you think ev demonstrates?
I think that we’re dealing with something other than just a thought experiment.
And the point of my example is not how to calculate a minimum, but rather how to maximize the information content per yes/no query. This requires a strategy.
heh. Let’s pretend that the way information is quantified doesn’t have anything to do with ev.
It demonstrates that a small subset of known evolutionary mechanisms result in the same behavior as seen in biological systems, in a relatively small number of generations with a very small population.
I get the impression that you are misunderstanding what happens in ev. Your thought experiment is equivalent to the calculation of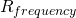 , the minimum information required to identify
, the minimum information required to identify  locations in a string of length
locations in a string of length 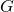 . This value depends solely on the problem configuration and does not change throughout a run. There is no “strategy” required.
. This value depends solely on the problem configuration and does not change throughout a run. There is no “strategy” required.
The interesting measurement is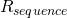 , the Shannon uncertainty of the binding sites. This evolves to and oscillates around
, the Shannon uncertainty of the binding sites. This evolves to and oscillates around 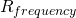 , despite having the potential to be much higher. The same behavior is seen in the biological systems that Dr. Schneider studied.
, despite having the potential to be much higher. The same behavior is seen in the biological systems that Dr. Schneider studied.
Given that, what is the point you’re trying to make?
What is the behavior that is seen in biological systems that is produced by the ev program? Binding site recognition?
Do you conclude that biological populations can evolve binding site recognition in a small number of generation in a very small population?
How is that distinguishable from magic?
That does not follow from anything I’ve written.