Subjects: Evolutionary computation. Information technology–Mathematics.1
Yes, Tom English was right to warn us not to buy the book until the authors establish that their mathematical analysis of search applies to models of evolution.
But some of us have bought (or borrowed) the book nevertheless. As Denyse O’Leary said: It is surprisingly easy to read. I suppose she is right, as long as you do not try to follow their conclusions, but accept it as Gospel truth.
In the thread Who thinks Introduction to Evolutionary Informatics should be on your summer reading list? at Uncommon Descent, there is a list of endorsements – and I have to wonder if everyone who endorsed the book actually read it. “Rigorous and humorous”? Really?
Dembski, Marks, and Ewert will never explain how their work applies to models of evolution. But why not create at list of things which are problematic (or at least strange) with the book itself? Here is a start (partly copied from UD):
- It is not a textbook, it is a tract: The authors expect their readers to know important verses of the Bible by heart (“Secondly we believe a la Romans 1:20 and like verses that the implications of this work in the apologetics of perception of meaning are profound”), but that they have not heard of the most common technical terms (“JPG: pronounced JAY-peg”). The maths is used not to enlighten, but to impress: it is not just preaching to the choir, it’s preaching to the choir in Latin.
- The nature of this book allows the authors to skip over all the problems of their ideas and omit difficult definitions: while they talk about “searches” for dozens and dozens of pages, they never define what a “search” is.
One of the most problematic sentences is on page 173: “We note, however, the choice of an [search] algorithm along with its parameters and initialization imposes a probability distribution over the search space”.
Does it really? They authors have tried to show this in a couple of ways in various papers, and each of their approaches seemed to be ridden with further problems. So, they just side-step this crucial bit of their theory. - The conclusion for the section on proportion betting seems to be wrong (Section 4.1.2.2.12 “†Loaded Die and Proportional Betting”.) The authors claim:
The performance of proportional betting is akin to that of a search algorithm. For proportional betting, you want to extract the maximum amount of money from the game in a single bet. In search, you wish to extract the maximum amount of information in a single query. The mathematics is identical.
But if there are two fields of equal size, and I lost my keys in the first one with probability 2/3, in the second one with probability 1/3, it makes sense to search the whole of the first field, and only afterwards the second one. On average, it takes longer to switch between the fields with probabilities 2/3 and 1/3, respectively (even if switching does not take any time) – that’s because the doubling rate parameter does not apply to this problem.

Mung,
As DEM’s central result is about probability distributions, it is a sine qua non for them to translate searches into such distributions: to find a probability distribution which is characteristic for a particular search (Dembski, Marks, 2010), to represent a search by a distribution (Dembski, Ewert , Marks, 2014), or to associate a search with a distribution (Dembski, 2014).
How does such a translation work? You have to define the term search in a (mathematical) way that allows for it. And that’s where DEM’s problems started.
Their definition in “The Search for a Search: Measuring the Information Cost of Higher Level Search” was very elegant by introducing an augmented space. It had the additional advantage that a search of length Q worked as well as Q random guesses (without repetition).
The tiny problem: the augmented space was not a probability space, so, what they thought to be a probability distribution representing the search wasn’t one.
Therefore, they introduced a new definition in 2014’s “A General Theory of Information Cost Incurred by Successful Search”. That one produced a probability distribution on the original space, but does not resemble the idea of a search as most of us would understand it. In contrast to their earlier work, the average of all searches of length Q would only work as well as a single random guess, not Q guesses! AFAIK, they just ignored this contradiction to their earlier work.
In fact, even performing a complete search, exhausting all the space, would on average not work better than a single guess – and that’s absurd.
How did they achieve this? Basically by separating the fitness function and the target. Imagine one favorite example of DEM: pirates looking for a treasure. After searching the whole island they have found their chest of gold and present it to you. And you tell them: “Oh no, that is not the treasure we were looking for. In fact, we have been looking for a red pea.” At which moment, they declare you mad and rightfully stab you….
I suppose that DEM are flattered, because of Schopenhauer’s three stages of truth:
They must have passed the first two stages, and their ideas are seen as trivial at last! Unfortunately for them, most ridiculous trivialities turn out to be not true – and that’s why they are opposed…
DiEb,
The most ridiculous of false trivialities is that improbability becomes information when expressed on a logarithmic scale.
Out of some necessity, which I don’t remember the details of, Panda’s Thumb moved from being a WordPress blog to being driven by a Github account, using the Disqus software to handle comments. The old comments exist, backed up, but there needs to be some work to convert them to the new system. The owner of PT is a junior faculty member with an active research lab, students, and a busy family life as well, so he is not able to do this right now. Ultimately the comments will return, but it has been slow to happen.
So, that is a bit distressing but … the comments are actually available in The Wayback Machine (at archive.org). Hooray for them! The ones for that thread are here:
https://web.archive.org/web/20150410203407/http://pandasthumb.org/archives/2015/03/fitness-surface.html#comments
and comments on any other thread (before the migration of PT) can be found by going to “archive.org”, searching for “Panda’s Thumb” and choosing a backup soon after the date of the thread. I think even the PT “Bathroom Wall”.
Joe Felsenstein,
Thanks! Unfortunately, at archive.org, I can only visit Comment-Panel-1 and Comment-Panel-6. Well, I’ll try it later again…
DiEb,
You’re right. Well, anyway we can get a small fraction of the comments. The others do exist on backups, I am told by the PT elite.
Seems to me that the best anyone could do is demonstrate that a mathematical model of evolution is compatible with the ToE or not. Claiming a model doesn’t work is no evidence that the phenomenon itself is impossible, just that you need a better model.
PS
And of course I’d also argue that evolution is directed by the bias provided by the niche. So DEM are wasting their time disproving undirected evolution! 🙂
And this is bad news for so many here at TSZ, including those persons named petrushka.
Because?
I agree.
What about ev? Also not a model of evolution?
Because you have people here claiming just the opposite. Seriously. Do you pay attention to the goings on here at all, lol?
People claimed that this or that algorithm isn’t a search algorithm because it has no target(s). TSP is a favorite of petrushka.
Not these days. We have Trump now. ID is an irrelevance.
My thinking is that evolution (the real thing) isn’t a search for anything. It’s a struggle for existence. I’d like to see someone model the zest for life.
First, what is primarily of interest in ev is not categorical success in coevolution of binding sites and a binding site recognizer, but instead the quantity of the reduction in empirical entropy (gain in information) of the nucleotides at the binding sites. Schneider began with a phenomenon known by observation of organisms. The theoretical account for it does not depend on the particular mechanism of binding site recognition. Schneider reproduced the phenomenon with an abstract binding site recognizer. Marks et al. say nothing about this. Dembski has been going at ev since 2000 or 2001, and I don’t recall seeing him give an explanation of what the model actually addresses.
The “target” is not specified independently of the evolutionary process. It is a crucial component of the model that fitness depends on the accuracy of binding site recognition. Schneider is not saying that the “problem” was independently given, and that an evolutionary process poofed into existence to solve it.
By the way, Marks et al. often say that the objective is “specified in advance” when they ought to say “specified independently.” I’m pretty sure that’s how they’ve confused themselves.
Well, the prototype is Dave Thomas, with his GA for Steiner trees. IIRC, he simply didn’t understand what Dembski (pre-Marks) meant by “target.”
As for TSP, we’ve got proofs that certain heuristics, under certain conditions (e.g., cities located in the Euclidean plane), produce a tour exceeding the optimal tour in length by at most a factor of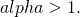 Obviously such results refer to an optimal tour that isn’t actually known, but nonetheless exists. And obviously (to me, anyway) you can define a target to be the set of all tours of length not exceeding the minimum by more than a factor of
Obviously such results refer to an optimal tour that isn’t actually known, but nonetheless exists. And obviously (to me, anyway) you can define a target to be the set of all tours of length not exceeding the minimum by more than a factor of 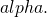
The thing that confuses lots of people about MDE is that they consider the association of costs/fitnesses/whatevers with possible solutions as part of the solution-generating process, not part of the problem. This means that the TSP problem, as understood by just about everyone in the world, is not solved by search, as defined by MDE. That is, the distances between cities are given in an instance of the problem. The input of the instance to a TSP solver is data, not information.
ETA: I guess MDE can argue that the assignment of lengths to paths, using the given distances on links between cities, is use of domain knowledge. But that’s pretty weird.
DiEb (delayed response):
My sentiments exactly. MDE presume that the reader believes already that there’s something to ID, and wants to learn about it. What I’ll add is that they know that they have the reader’s trust, and that they wantonly violate it.
DiEb:
On average, how many Bible verses per chapter?
The OP is just chock full of irrelevant nitpicking and this is just yet another example.
This comment is irrelevant nitpicking.
To make my point, a single instance was enough.
You may disagree with me on the target audience of this book. But the critique of the content is valid.
DiEb (delayed response):
What’s truly pathetic about this is that they’re contradicting what they wrote a few paragraphs earlier. Proportional betting maximizes the doubling rate of wealth when you allocate all of your wealth on each and every wager in a succession of wagers.
Never ever ever?
I am not sure I know what this means. I have seen you write it twice.
Does anyone?
And I don’t see how your objection makes any sense. For something to constitute a search it can only have a favorable outcome? Every generation of an EA must produce candidate solutions are are improved versions of previous candidates else it’s not a search?
Why can’t a process that searches for the poorest performance be a search? I mean that sounds just like evolution to me. Find the least fit and get rid of them.
The definition that I gave didn’t restrict “desired performance” to “improved performance.”
And DEM’s usage seems to me to make perfect sense in the context of search for a search. Certainly you don’t start out knowing which searches perform better than others without searching amongst alternatives which perform worse and not better.
I think he’s trying to distinguish between real biological evolution and programs like Avida.
DEM write, “The success of Avida is not due to the evolutionary algorithm, but to sources of information embedded in the computer program.”
Never ever ever?
Footnote 9.
David B. Fogel, Evolutionary Computation: Toward a New Philosophy of Machine Intelligence, 3rd edition (Wiley-IEEE Press, 2005).
Russell D. Reed and Robert J. Marks II, “An Evolutionary Algorithm for Function Inversion and Boundary Marking.” Proceedings of the IEEE International Conference on Evolutionary Computation, pp. 794– 797, November 26– 30 (1995).
Then one could say that the success of evolution is due to the information embedded in the fitness landscape.
The problems with this way of thinking are:
(1) it depends on a bogus notion of “information”;
(2) the supposed “embedded information” doesn’t just drop out by itself.
Neil, I’m not sure what your point is. But I’ll ask you the same question I asked Rumraket. Why did the authors of the Avida paper decide to reward longer genome lengths rather than shorter genome lengths?
ETA: And why did Tom and his co-author fail to mention this in their analysis of Avida?
I don’t read minds.
Also, I agree with those who point out that such programs are not simulations of evolution. They are tests or demonstrations of the abilities of some of the processes involved in evolution.
What process, or processes, did Avida test?
Best ask someone who is familiar with the program. I haven’t studied it.
So which programs did you have in mind when you wrote your response?
Neil:
Perhaps you didn’t have any program in mind.
Can we call that a Rickert?
The broad class of programs that are said to be using the genetic algorithm (or similar description).
I don’t have to be familiar with individual programs to have an opinion about a broad class of programs.
So it’s sort of like unicorns then. You don’t actually have to see one to believe they exist.
More specifically, they test some of the claims made against evolution, particularly the arguments made on the basis of probability. Such arguments as Dembski’s and Behe’s are abstract mathematical arguments, and can be tested as mathematical claims, regardless of whether biology is being modeled.
Meanwhile petrushka continues to maintain that the TSP has no targets and cannot therefore be solved by any search algorithm.
You are aware that we are talking about mathematical or scientific definitions? Stating that “The iterative process that looks for a successful design is dubbed computer search” is as useful in the context of this book as defining a fridge as a “white box with food in it” in a book on thermodynamics for laymen.
Kicking a rock repeatedly while praying for an insight would be a computer search!
But it looks so alike!
I got the impression that the last paragraph has nothing to do with anything said before.
1) In which way is Evolutionary Search a special case of Multiple Agent Search? For a definition, this should be specified.
2) One of the best known evolutionary algorithms is EA (1+1) (one parent, one child, only mutations, best of child and parent is the next generation). AFAIK, this algorithm is used in an implementation of Dawkins’s WEASEL which was televised. That’s not a Multiple Agent Search!
DiEb:
I began a response to Mung, but abandoned it. I was going to explain, as kindly as I knew how, that anyone who regards what he quoted as a definition — I’m sure that he actually does — is living in a different world than we are. In all honesty, that was what came immediately to mind when I read his comment. And the more I pondered the matter, the more I sensed the futility of trying to straighten things out.
1 + 1 = 2. Oh, you evolutionists are so irrational.
By the way, the phrase I recall from 1995 is Multiple Agent Stochastic Search. [ETA: Evidently it was used only by a friend of mine. I get only a thousand Google hits for “multiple agent search.”]
Under biological interpretation, the target is not a goal, but instead an attribute of the evolutionary process.
Only because biologists refuse to use terminology which is true. More evo-speak to cover their tracks.
A target is a target, not a result.
That brings something else annoying to my mind: the biography. So, DEM make the statement:
Their source for this claim:
We get an article by Bob Marks which – as far as I can see – does not mention either “evolutionary search” nor “multiple agent search”, and a book without a page number! The reader is supposed to look through 200+ pages for whatever DEM meant – as “evolutionary search” and “multiple agent search” don’t appear in the index!
Or take entry number 30 in Chapter 6:
That could be any of five papers mentioned before in 1-29 – good luck with searching those! Well, at least the biography looks impressive…
This sounds like what keiths does.
DiEb,
You mean bibliography.
Using Google Books, I find neither “multiple agent search” nor “multi-agent search” in David Fogel’s book. I know David’s work up to 2004 pretty well, and it’s not a term I recall him using.
Searching for inauthor:Fogel “multiple agent search” in Google scholar, I get only two hits, one of which is the book by MDE, and the other of which is a paper by the friend I mentioned above, John McDonnell (with two coauthors).
There are more hits for inauthor:fogel “multi-agent search” (again, a number of them associated with John McDonnell and Don Waagen). But there’s no indication that Fogel himself has used the term.
This is not characteristic of Dembski, when he works alone. Evidently Marks is highly impressionistic in his scholarship (scare quotes suppressed). I’ve noticed also that he regards citations of related work not as a scholarly obligation, but instead as a favor you do your buddies (to drive up their citation counts). I’m not his buddy anymore, so he doesn’t have to cite my work anymore. Of course, he’s big into self-citation. He can work a reference to his handbook on the Fourier transform into just about any paper.
The worst case was in the first publication of Dembski and Marks. They decided that Dawkins’s Weasel was partitioned search. So they wrote the term partitioned search, with emphasis as I just have, and followed it immediately with a reference to The Blind Watchmaker. Of course, Dawkins neither used that term nor described what they called partitioned search.
As for “multiple agent search,” Marks probably intends to lump evolutionary optimization (about which he knows little) with particle swarm optimization (about which he knows considerably more) in order to make a greater authority of himself. I’m sure that, deep down, he recognizes himself as a bombastic old ass, pronouncing on a wide range of topics he never bothered to study.
If you understand that it’s bad behavior on blogs, then you ought to have some idea of how atrocious it is in scholarly publications.
I have as equally little faith in the scholarly publication system. I am confident that the peer-review process is just as biased, and meaningless as things posted online.
Tom English,
Thanks for your thorough analysis! Hard to imagine that one of the “humble authors” (as DEM style themselves throughout the book) could be prone to bombast….
(Bibliography was the word I was looking for *blushes*)
That explains something about one paragraph (p. 173) with which I took umbrage in the first place:
Particle swarm, conjugate gradient descent and Levenberg-Marquardt search are not described in the book, they appear only in a table of “some search algorithms” on p. 58. Now it’s clear why the particle swarm made it into this absolutely unnecessary enumeration! I’d love to see how the “imposed probability” is calculated for a Levenberg-Marquardt optimization using the damping parameters…