Defending the validity and significance of the new theorem “Fundamental Theorem of Natural Selection With Mutations, Part II: Our Mutation-Selection Model
– Bill Basener and John Sanford
Joe Felsenstein and Michael Lynch (JF and ML) wrote a blog post, “Does Basener and Sanford’s model of mutation vs selection show that deleterious mutations are unstoppable?” Their post is thoughtful and we are glad to continue the dialogue. We previously wrote a first part of a response to their post, focusing on the impact of R. A. Fisher’s work. This is the second part of our response, focusing on the modelling and mathematics. Our paper can be found at: https://link.springer.com/article/10.1007/s00285-017-1190-x
First, a short background on our paper:
The primary thesis of our paper is that Fisher was wrong, in a fundamental way, in his belief that his theorem (“The Fundamental Theorem of Natural Selection”), implied the certainty of ongoing fitness increase. His claim was that mutations continually provide variance, and selection turns the variance into fitness increase. Central to his logic was that collectively; mutations have a net zero effect on fitness. While Fisher assumed mutations are collectively fitness-neutral, it is now known that the vast majority of mutations are deleterious. So mutations can potentially push fitness down – even in the presence of selection.
Additionally, we provided a new mathematical model for the process of mutation and selection over time, which comes in an infinite population version and a finite population version. The infinite population version uses a classical differential equations mutation/selection framework, with multiple reproducing subpopulations and mutations occurring between subpopulations, but incorporating a probabilistic distribution for mutation effects. The finite version is obtained by adding the constraint that any subpopulation with less than one organism is assumed to have no members.
Our model is backed by a literature review in Section 2 of our paper (covering 9 pages with 71 citations), with Section 2.2 discussing previous infinite populations models and Section 2.3 focusing on finite ones. Our model is new in that it includes an arbitrary distribution of mutational effects, and we do not assume mutations are 50/50 beneficial /deleterious (as did Fisher), and we did not assume that all mutations have the same fixed effect (as with Lynch’s finite population models).
Part II: Our Mutation-Selection Model:
Regarding our model, JF and ML describe it as follows:
“Basener and Sanford show equations, mostly mostly taken from a paper by Claus Wilke, for changes in genotype frequencies in a haploid, asexual species experiencing mutation and natural selection. They keep track of the distribution of the values of fitness on a continuous scale time scale. Genotypes at different values of the fitness scale have different birth rates. There is a distribution of fitness effects of mutations, as displacements on the fitness scale. An important detail is that the genotypes are haploid and asexual — they have no recombination, so they do not mate.” – Felsenstein and Lynch
This is an accurate description of our infinite population model. However, as we shall discuss shortly, they do not address our finite population version.
As a first minor point of correction, our equations are not taken from the cited paper by Claude Wilke. The Wilke paper is a nice review article, showing that two separate but significant lines of research (classic population genetics mutation-selection models and the Quasispecies or Replicator equations used in virus evolution) are mathematically equivalent, but no new equations are provided. Background support for our model is provided in Section 2, which as mentioned above is 9 pages in our paper and has 71 citations. The first-principles derivation of our infinite model, from standard population modeling principles, is given in Section 3.1 and the only previous model referenced in that section is the “special example” of Fisher’s theorem given in Crow and Kimura. The equations that JF and ML say we took from the Wilke paper were used (in equivalent mathematical forms) to prove a version of Fisher’s FTNS in Population Genetics by Hamilton (p.204), in An Introduction to Population Genetics Theory by Crow and Kimura (p. 10), and in The Mathematics of Darwin’s Legacy by P Schuster (p. 39).
In their analysis of our infinite model, JF and ML correctly point out that our model is haploid and asexual. This is true, and is the correct setting for our analysis of Fisher’s FTNS, and is the format used by Crow and Kimura, by Hamilton, and by P Schuster cited above. (The Crow-Kimura model is presented from a classical haploid asexual mutation-selection population genetics model while the Schuster Chapter motivates using a Replicator Equation; hence our citation of Wilke showing these two historically relevant lines of work are mathematically equivalent.) Lynch’s 1990 paper Mutation load and the survival of small populations (1990) similarly begins with a model focusing on asexual reproduction, and his model was extended to populations with sexual reproduction in Mutational meltdown in sexual populations (1995), where he showed results which “indicate that mutation accumulation in small, random-mating monoecious populations can lead to mean extinction times less than a few hundred to a few thousand years.” To the extent that JF and ML urge caution about using our model to make conclusions regarding sexual populations, we certainly agree. To any extent they dismiss our model because it is for asexual haploid populations, we disagree: this is the standard setting for Fisher’s FTNS, and is a natural simple case for first work that should be followed up with asexual models for extension to asexual populations which were not addressed in our paper.
JF and ML raise a question in the title of their post, “Does Basener and Sanford’s model of mutation selection show that deleterious mutations are unstoppable?” We do not actually make this claim, and this question is not directly addressed in our paper – we show Fisher’s claim of certain fitness increase is false due to mutation effects, and then give a model (with a finite and infinite version) and associated theorem that facilitates studying under what conditions fitness increases or decreases. We provide numerical simulations using the net-neutral-mutational-effect assumption inline with Fisher that shows fitness increase, and a simulation using the net-deleterious-mutational-effect from Kimura that undergoes continual fitness decline to demonstrate the importance of Fisher’s reliance on net-neutral mutational effects. Our paper provides a tool to better understand selection in the presence of deleterious mutations (actually more than that since we incorporate beneficial ones too), but does not pose any general answers for real biological populations other than saying they can go up or down. We are convinced that there is a very wide parameter space where fitness should be expected to decline, as ML has reported in many of his papers. The question of what parameters are required for equilibrium or continuous fitness gain is a subject we hope to address in the future.
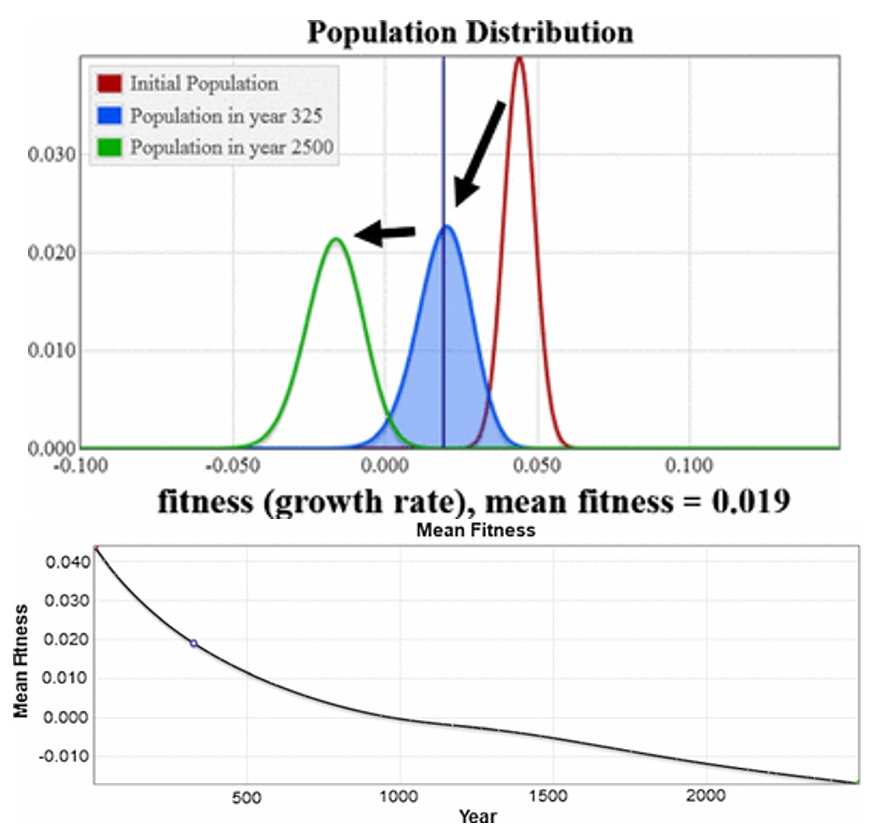
A focal point for JF and ML is our numerical simulation presented in Section 5.4. All of our simulations use our finite population model. The simulations in 5.1-5.3 either omit mutations or use a symmetric Gaussian distribution which is what Fisher considered for mutational effects, and the simulation in Section 5.4 uses the Gamma distribution for mutational effects from (Kimura 1979) with some beneficial ones added. The result is a fitness distribution for the population that declines steadily down through negative values, shown below.
Felsenstein and Lynch remark:
“…in their final case, which they argue is more realistic, there are mostly deleterious mutations. The startling outcome in the simulation in that case is their absence of an equilibrium between mutation and selection. Instead the deleterious mutations go to fixation in the population, and the mean fitness of the population steadily declines.”
They are correct in their description of the outcome. They find this result ‘startling.’ If this result were output from an infinite population it would be extremely startling; we provide a proof in Section 4 (Analytic Solutions) that the infinite version of our model goes to mutation-selection equilibrium. This is a classic result in this class of mutation/selection models. To explain the difference between output from our finite and our infinite models, we provide the following video: (https://www.youtube.com/watch?v=bBb4jPmctFk, The infinite model is on the left and goes to the guaranteed mutation–selection balance equilibrium while the finite one does not. All parameter values are equal.)
 The two versions of our model are described in Section 3:
The two versions of our model are described in Section 3:
“The model can be treated as an infinite population model using the differential equation in Eq. (3.2), or as a finite population model when any subpopulation with less than one organism is rounded down. Thus, we use the first principles approach to modeling from the previous infinite population models, but incorporate the flexibility of the previous finite ones.”
We also describe the finite models in Section 5:
“To remain biologically realistic, we assume a finite population: any subpopulation Pi that contains less than some fraction of the population is assumed to contain zero organisms. For the numerical simulations, we set Pi=0 whenever Pi is less than 10−9 of the total population. This approximates a total population of 109 and eliminates any subpopulation with less than a single organism. The only case where this made an observable difference was Sect. 5.4. In that case, without the finite-population condition subpopulations remain viable even when they contain less than a fraction of an organism. As a result, extremely small, biologically nonsensical, populations control the observed results and obscure the effect of mutations on the population as a whole.”
In Section 4 we provide the formula for the mutation-selection equilibria for the infinite model and discuss the role of the infinite assumption:
“The sole equilibrium solution is the P=0, and all other solutions will be asymptotic to the eigenvector corresponding to the largest eigenvalue of W. By treating the system as a differential equation, we are implicitly assuming an infinite population; in this model, each Pi will be non-zero positive, but can be arbitrarily small. … These systems are considered infinite populations in part because each subpopulation Pi remains non-zero, regardless of how small Pi is compared to the total population. In the numerical simulations of Sect. 5, we address this be setting any subpopulation with sufficiently small fraction of the total population to zero.”
The theorem and accompanying formula provided in Section 4 is a classic result in mutation-selection models (see Burger 1989). It can be used to prove mathematically that our model is not an infinite model. The simulation in the accompanying video above shows the equilibrium and asymptotic eigenvector for the matrix W. If our model were an infinite model, it would have to be asymptotic to this same equilibrium (since the finite and infinite models in the video have the same matrix W), but it is not. Thus, our finite model is not an infinite model via proof by contradiction (assuming one trusts the output shown in the video).
The role of the finite assumption and its implications for mutation-selection balance are again described in the first paragraph to Section 3:
“In mutation–selection population models, as described in Sect. 2, there is a balance between the downward effects of deleterious mutations and upward effect of selection that balances out in infinite population models but not in finite population models. Our main theorem, Theorem 2, provides the rate of change of mean fitness into two terms, the first being the genetic variance and the second being a decrease in fitness from mutations, and the two are not equal.”
Not only is the role of the finite assumption pivotal in our paper, our main theorem (FTNSWM) provides insight into when fitness is increasing versus decreasing even when you do not have a guaranteed global attracting equilibrium. (Our theorem is exact for infinite populations and approximate for finite ones.)
Here is the analysis from JF and ML on why the population in our simulation from Section 5.4 experiences continual decrease:
“Why does that happen? For deleterious mutations in large populations, we typically see them come to a low equilibrium frequency reflecting a balance between mutation and selection. But they’re not doing that at high mutation rates!
The key is the absence of recombination in these clonally-reproducing haploid organisms.”
JF and ML ascribe the continual decline in fitness to the asexual haploid reproduction model and high mutation rates. The infinite asexual haploid reproduction model is mathematically guaranteed to go to equilibrium, so it seems counter-logical for them to use this to explain the lack of equilibrium if they believe that ours is an infinite population model.
Their comments on realistic mutation rates are absolutely important, and conclusions extending our model about general populations need to be done using a proper, rigorous, thorough exploration of parameters including mutation rates. But the mutation rates are not causing the ongoing continual decline; the infinite model with these same rates goes to mutation-selection equilibrium with mean fitness of 0.039 as shown in the video above.
JF and ML continue by putting parameters from our model through “the usual calculations of the balance between mutation and selection” (their words). But these do not apply because they are not derived from our model, but generally derive from infinite models – often considering a single mutation in isolation. Moreover, if our model results deviate from the usual calculations, it makes our model new, possibly interesting, but not wrong. (Again, we believe a proper evaluation on parameters including mutation rates should be done if general conclusions are to be drawn from our model. It is valid to evaluate our model either by evaluating the assumptions in its derivation or by comparing results to physical measurements, but not to challenge the model because it disagrees with other models.)
Their usual calculations for balance and selection assume our selection coefficient is “around 0.001”. But we do not have a fixed selection coefficient. We use a probability distribution to model mutational effects (specifically the Gamma distribution from Kimura 1979) with selection occurring as competition between different fitness, which is far more realistic than a single selection coefficient. The mean change in fitness in this distribution is 0.001, but most mutations will have an effect less than this value because the Gamma distribution is skewed (its median is less than its mean). As stated in Mutational meltdown in sexual populations (1995), the value of a selection coefficient (impact on fitness by a mutation) greatly impacts the decrease in fitness from mutation accumulation:
“It is now well established that mutations with small, but intermediate, deleterious effects cause the most cumulative damage to populations (Kimura et al. 1963; Gabriel et al. 1993; Charlesworth et al. 1993). Mutations with very large effects are eliminated efficiently by selection and have essentially no chance of fixation, whereas neutral mutations have no influence on individual fitness. The diffusion theory developed by Lande (1994) suggests that the value of s that minimizes the time to extinction, that is, that does the most damage, is s* = 0.4/Ne. T”
Our model is a finite model with mutations occurring probabilistically across a realistic distribution of effects on fitness, which is a significant deviation from most previous models. We use a novel method for finite populations, which enables us to use the rigorous derivation of standard mutation-selection infinite population models, enables us to apply the formula for change in fitness due to selection (upward force) vs mutation (downward force) proven in our main theorem, and enables us to use an arbitrary probability distribution for mutational effects.
JF and ML comment:
“So there is really nothing new here.”
And then conclude with statements about what would change in the output from our model if certain changes were made.
“If Basener and Sanford’s simulation allowed recombination between the genes, the outcome would be very different — there would be an equilibrium gene frequency at each locus, with no tendency of the mutant alleles at the individual loci to rise to fixation.
If selection acted individually at each locus, with growth rates for each haploid genotype being added across loci, a similar result would be expected, even without recombination. But in the Basener/Stanford simulation the fitnesses do not add — instead they generate linkage disequilibrium, in this case negative associations that leave us with selection at the different loci opposing each other. Add in recombination, and there would be a dramatically different, and much more conventional, result.”
Clearly, we believe that JF and ML misunderstand our finite model and its implications. However, and this is significant, we agree with them regarding the answer to the question they pose in the title of their post, Does Basener and Sanford’s model of mutation vs selection show that deleterious mutations are unstoppable?. Our paper does not show that they are unstoppable, and does not try to. It is significant that JF and ML raise this question.
Our paper does show that the buildup of deleterious mutations can be significant, but this was known before; our result in the simulation in Sec 5.4 is consistent with results from Lynch. Our paper shows that this fitness decline occurs in the context of Fisher’s model when realistic factors (realistic mutation distribution and finite population) are incorporated. It does show that Fisher’s conclusions about application of his FTNS is false, and in a way so fundamental that his FTNS gives no real support for the Neo-Darwinian Theory. We provide a new model and new analytic tools that can be used to examine whether fitness is going up or down, and these can incorporate realistic factors in ways not previously considered.
Application of any model to real biological populations is a big undertaking, and must be done with impartial use of the ranges for previously published ranges for parameter values (such as mutation rates and mutation effects), and a consideration of the explicit and implicit assumptions in the model derivation and their relevance to reality.
A good example of examining competing hypothesis using ecological economics population models I (Bill B) developed for collapse in ancient human civilizations is given in The slow demise of Easter Island: insights from a modeling investigation. This is an extremely hotly debated topic with intelligent and qualified camps with differing views, including anthropologist Terry Hunt from the University of Hawaii who has spent his career studying Polynesian-type islands, and the high-profile Jared Diamond from UCLA with his Guns, Germs, and Steel approach. You can read some of the online debate here, here, and here. And if you want to see academic discussion gone really really bad, read this paper. (See my very measured response to a newspaper interview here. I am not a fan of jumping to conclusions regardless of prior belief.) But the real point is, despite the amount of personal views and emotion, The Slow Demise paper is a good model for testing population models, basing conclusions on thorough background exposition, examination of the derivation and components of a model, and then examination of the variety of possible outcomes.
Conclusions:
- A. Fisher was one of the three founders of population genetics, and is considered by many to be the principle founder. His FTNS theorem has been considered a significant and rigorous support for the Neo-Darwinian Theory.
- Fisher’s theorem in fact does not provide support for the Neo-Darwinian Theory. The upward pressure of selection on fitness cannot be realistically considered apart from the downward effect of mutations.
- JF and ML state that our paper does not show that deleterious mutations are unstoppable. We agree; our paper shows what can happen, not what must happen. Conclusions about what our model predicts, given biologically realistic parameters, is a separate undertaking.
- JF and ML gave an accurate description of our infinite model, but misunderstood the finite model, apparently because it is a new form of finite model.
- Our finite model is constructed in a new manner. We can prove mathematically that this is not an infinite model. Novel attributes include the use of a realistic destruction of mutational effects, use of classic form for instantaneous rates of change in a finite model, and analysis with our new FTNSWM Theorem.
- JF and ML gave analysis using standard computations from infinite models and with selection happening separately at each locus, which is not relevant to our model because ours is not an infinite model.
- JF and ML conclude from their standard computations that “there is really nothing new here.” It is ironic that they fail to recognize our new finite model, and then declare that there is nothing new.
- They conclude by claiming that if our model were modified to include recombination, the result would be more conventional. We do not think it is possible to know the outcome of a model without building it. This work will follow.
In short, we agree with JF and ML that our paper does not show that deleterious mutations necessarily result in declining fitness. However, we have clearly falsified the converse claim, which is that genetic variance plus selection necessarily result in increasing fitness.
If Joe F and Michael L write a response, we politely request that they provide quotes from our paper that support their claims that we argue that fisher’s FTNS “is the basis for all subsequent theory in population genetics.” (Full sentence: “This is presented as correcting R.A. Fisher’s 1930 “Fundamental Theorem of Natural Selection”, which they argue is the basis for all subsequent theory in population genetics.”) We also invite them to clarify if our paper claims that “deleterious mutations are unstoppable” as seems to be implied in the title of their article, and provide quotes from the paper if they believe we support that premise.
Final Comment: Please forgive this minor soap box issue of mine, but I want to encourage careful interpretation of mathematical models, especially regarding assumptions and parameters that are not fully known. Mathematical models are not reality. Fisher made a mistake in his assumptions applying his theorem, and it led to some bad conclusions for 50-100 years. Here is a quote from the third paragraph of Section 2 of our paper:
“Every model is only an approximation of some isolated subset of reality, and each model is only useful insofar as it: (1) includes the variables and rules to be studied and: (2) the rules governing change in the model accurately approximate the most important factors affecting change in reality. Simple rules make a model more mathematically tractable, but at the cost of utility as a useful model of reality. The general goal is to have rules that are as simple as possible, and yet capture all the driving factors contributing to the phenomena to be studied. In using a model to make general statements about behavior in reality, it is essential to consider the built-in assumptions implicit in the structure of the rules in a model.”
Here is a related quote from Okasha, that J-Mac posted recently:
“It is clear that population genetics models rely on assumptions known to be false, and are subject to the realism / tractability trade-off. The simplest population-genetic models assume random mating, non-overlapping generations, infinite population size, perfect Mendelian segregation, frequency-independent genotype fitnesses, and the absence of stochastic effects; it is very unlikely (and in the case of the infinite population assumption, impossible) that any of these assumptions hold true of any actual biological population. More realistic models, that relax one of more of the above assumptions, have been constructed, but they are invariably much harder to analyze. It is an interesting historical question whether these ‘standard’ population-genetic assumptions were originally made because they simplified the mathematics, or because they were believed to be a reasonable approximation to reality, or both. This question is taken up by Morrison (2004) in relation to Fisher’s early population-genetic work. “ Samir Okasha 2006/2012

Bill Basener:
So it’s biologically realistic to have 1.5 individuals of one type, but not 0.99 individuals of another type? Why did you not round quantities to the nearest integers? You haven’t even truncated consistently.
Perhaps it is for want of imagination, but I cannot come up with a justification for the approach you have taken. It looks like an ugly trick for reducing the diversity of the population. I do not want to hear from you, in response, “Oh, well, you might do it other ways.” I want to know your rationale. Why did you decide to take the particular approach that you did? The decision was anything but arbitrary.
I don’t know much about population genetics, but I do know that a sensible approach to obtaining a finite population is random sampling of the infinite population.
So I reasonably guess that the sum of proportions is not small, which is to say that when you zero
is not small, which is to say that when you zero  the sum over all
the sum over all  is not close to 1. This would say to me that your DE model and your simulation model really don’t have much to do with one another.
is not close to 1. This would say to me that your DE model and your simulation model really don’t have much to do with one another.
Edit: Changed 0 to in last paragraph.
in last paragraph.
Bill Basener:
Patent garbage, beginning with the fact that 2030 is 12 years in the future. Your “evolutionists are religious too” thesis wears the thinnest of veils.
One of the foundations of Fisher’s 1930 work was in 1918 which Bill cited, that’s about 100 years ago give or take a few months.
Tom,
This was one of Fisher’s 1918 papers that have the assumptions that Bill was commenting on his soap box.
https://en.wikipedia.org/wiki/The_Correlation_between_Relatives_on_the_Supposition_of_Mendelian_Inheritance
2018 – 1918 = 100
Tom, that’s a non-content critique. Price put Fisher’s work in good perspective a number of years ago so you could find reason to justify a number near 50 years. People are probably still making bad conclusions from it, so you could put the data sometime in the future. Sal’s response is a good as any. Regardless, I’m interested in sharing knowledge, not nitpicking each other’s words. I can’t see any reason that matters.
Hi Tom,
Your request for justification is fine. It will take some time to write something. In the mean time I can tell you we didn’t choose this method to get a desired result. The result of our output is consistent with previous finite population models. No tricks are needed for that. The method you are familiar with of taking a finite random sample would be good too.
And another tune will be sung in presentations to creationist audiences. Your sycophants are already selling your paper as if it has somehow falsified evolution. You will no doubt be busy in the coming months throwing a wet blanket on that fire, telling the poor rubes that they should not take your mere mathematical models that far in conclusion?
Whatever one decides about the paper, it may arrive at a conclusion that even Michael Lynch himself would agree with:
So, for Michael Lynch and Joe Felsenstein objecting that recombination supposedly fixes the issues in Bill and John’s simulation, apparently it doesn’t fix the problem Lynch is pointing out, which ironically is an appeal for genetic intervention (aka man-made intelligent design).
So I can’t see how Michael Lynch can be saying the simulation reaches invalid conclusions about declining fitness, especially in populations with recombination like humans! At best maybe the inference is wrong (if at all), but that has yet to be demonstrated.
Taking the specific case of a huge drop in the mortality rates of Homo sapiens due to the inventions of systematic agriculture, industrialization, and modern medical science, and extending them to the biosphere as a whole, is a rather absurd extrapolation.
The fact that deleterious mutations might be accumulating in human populations because we have become so good at avoiding the “natural” deaths that would normally purge a substantial fraction of such mutations in the wild, does not mean this is somehow the “normal” state of affairs. Nor does the fact that such accumulations could very well be happening to us now and in recent history, mean that it was always in effect.
My background is mathematical dynamical systems, differential equations, and statistics. The method I chose eliminates the unrealistic small subpopulations while keeping the model deterministic, which is preferred by mathematicians. (Taking a finite random sample as you suggest would be non-deterministic, and move the model into the class of agent-based models). I don’t know that it needs to be deterministic, but deterministic models are amenable to analysis by rigorous proofs, which is in my background (see my textbook here). In my work in statistics, we often reject entirely options that have a probability below some threshold. This is a principle that I have used many times in machine learning / signal processing software called Occam’s window.
I like your random finite sample method too. It would take longer to run (have to take a random sample of 10^9 points each year for 2500 years) and you would not get the same exact result every time. The rounding each subpopulation to an integer value seems fine too. I expect you would get similar results with each, but would wait to test them before declaring anything conclusive. (I’ll consider a paper testing them – I do like your idea.) But, like I said, there was no tricks needed to get our result. It is consistent with previous finite models; we just showed you could get there starting with Fisher’s framework.
The question arises about the deleterious/beneficial ratio. There is one scenario where this is moot, namely the sheer number of deleterious mutations per individual per generation. This is the mutation load argument developed by Hermann Muller and discussed in Joe Felsenstein’s book and advocated by Dan Graur. So straining about which deleterious/beneficial ratio is the right one is moot if the absolute count of deleterious is high enough.
So I see the criticisms of Bill and John’s paper as straining at gnats and letting camels through. I wrote this somewhere else earlier, and I’ll simply repeat it:
Even aside from Basener and Sanford, others including Nobel Prize winner Hermann Muller pointed out the human race cannot tolerate very many mutations per individual per generation. The number Muller arrived at was about 1 bad mutation per generation per individual as the limit the human genome can tolerate.
Additionally, so what if an individual has a good mutation if he has 10 bad to go with it. This is like have a slight increase in intelligence while having 10 heritable diseases to go with it. You go one step forward and ten steps back.
Can natural selection arrest the problem? Only if there are enough reproductive resources relative to the number of offspring per couple.
For human populations there was something published by Nachman and Crowell and Eyre-Walker and Keightley using a Poisson distribution as reasonable model for the probability of a eugenically clean individual appearing in the face of various mutation rates.
If it is improbable that an eugenically clean kid can be reproduced by a couple, this makes it hard to weed out the bad. So this is an alternative way to arrive at Muller’s conclusions, which are also Sanford and Basener’s conclusions, and really everyone else’s conclusions as summarized by Dan Gruar: “If ENCODE is right, evolution is wrong.”
This is a simpler argument than the one Basener and Sanford put forward, but to Sanford’s credit, he’s also put the simpler version in his book Genetic Entropy, although the following derivation isn’t in his book, it’s something I ginned up myself. 🙂
So how can we estimate the probability a kid can be born with no defective mutations?
The following derivation was confirmed in Kimrua’s paper (see eqn. 1.4)
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1211299/pdf/1337.pdf
which Nachman and Crowell, and Eyre-Walker and Keightley reference as well.
So now the details:
let U = mutation rate (per individual per generation)
P(0,U) = probability of individual having no mutation under a mutation rate U (eugenically the best)
P(1,U) = probability of individual having 1 mutation under a mutation rate U
P(2,U) = probability of individual having 2 mutations under a mutation rate U
etc.
The wiki definition of Poisson distribution is:
to conform the wiki formula with evolutionary literature let
and
Because P(0,U) = probability of individual having no mutation under a mutation rate U (eugenically the best), we can find the probability the eugenically best individual emerges by letting:
which yields
Given the Poisson distribution is a discrete probability distribution, the following idealization must hold:
thus
thus subtracting P(0,U) from both sides
thus simplifying
On inspection, the left hand side of the above equation must be the percent of offspring that have at least 1 new mutation. Noting gain that , the above equation reduces to the following:
, the above equation reduces to the following:
which is in full agreement with Nachman and Crowell’s equation in the very last paragraph and in full agreement with an article in Nature: High genomic deleterious mutation rates in homonids by Eyre-Walker and Keightley, paragraph 2.
http://www.lifesci.sussex.ac.uk/CSE/members/aeyrewalker/pdfs/EWNature99.pdf
The simplicity and elegance of the final result is astonishing, and simplicity and elegance lend force to arguments.
So what does this mean? If the bad mutation rate is 6 per individual per generation (more conservative than Gruar’s estimate if ENCODE is right), using that formula, the chances that a eugenically “ideal” offspring will emerge is:
This would imply each parent needs to procreate the following number of kids on average just to get 1 eugenically fit kid:
Or equivalently each couple needs to procreate the following number of kids on average just to get 1 eugenically fit kid:
For humanity to survive, even after each couple has 807 kids on average, we still have to make the further utterly unrealistic assumption that the eugenically “ideal” offspring are the only survivors of a selective process.
Hence, it is absurd to think humanity can purge the bad out of its populations — the bad just keeps getting worse.
In truth, since most mutations are of nearly neutral effect, most of the damaged offspring will reproduce, and the probability of a eugenically ideal line of offspring approaches zero over time.
Muller’s number of only 1 new bad mutations per generation per individual. So if anything I understated my case.
There are some “fixes” to the problem suggested by Crow and Kondrashov. I suggested my fix. But the bottom line is to look at what is actually happening to the human genome over time. Are we getting dumber and sicker? I think so. It’s sad.
We can test Basener and Sanford’s prediction by observing whether human heritable diseases continue to increase with each generation. Whether their derivation is right or not, some of their conclusions are observationally and experimentally testable.
Regarding Joe Felsenstein and Micheal Lynch’s objection regarding recombination, Bill cited something by lynch. It is worth noting:
Mutational meltdown in sexual populations (1995) by Michael Lynch
http://onlinelibrary.wiley.com/doi/10.1111/j.1558-5646.1995.tb04434.x/full
So again, I’m not so sure appeals to recombination are a panacea for preventing meltdown. Perhaps at best, the issue is whether an inference to this conclusion can be made with the revision to Fisher’s formula or whether it is the domain of another set of equations. I don’t know.
Apart from the obvious mathematical blunder, there are two simple counterpoints:
1) human males produce considerably more offspring than that;
2) if you were right, we would have gone extinct, as would the many animal species which have much shorter generation times.
stcordova,
So according to Lynches theory any beneficial mutation will eventually become part of a series of changes that break the genome down into non function. Is this correct? In this case the term “beneficial mutation” is only a serendipitous situation that is temporary and eventually becomes a part of a group of mutations that as a group are delirious.
No.
Hypothetically to seed a simulation, OK, but after that offspring should be modeled as a descendant of a parent (which implies inheritance of some characteristic), not a random sample from an infinite population where we force a parent to “adopt” a genome that doesn’t have heritable resemblance to the parents.
But then, if we simulate things this way, how is that really different that just starting out with a population of individuals with some random variation to start with!
Bill Basener:
Your software has at least one major defect, impacting significantly the results you obtain, and several minor defects. I will give the details in a post of my own, when I am through going over your code.
As for your general approach, I do not see the value in initializing a system in a state that, with high probability, it does not enter when operating “freely,” according to its own dynamics. (I did the same in my post “Evo-Info 3: Evolution Is Not Search,” but only for pedagogical purposes.) It seems to me that what you should be doing in each generation is to convolve the distribution
is to convolve the distribution  (my notation) over fitness changes with the distribution
(my notation) over fitness changes with the distribution  over fitnesses. (You are approximating the convolution with your matrix multiplication, as I see it, but I’m not yet convinced that the approximation is good.) I say that the “natural” initialization is to put all of the probability mass on zero in
over fitnesses. (You are approximating the convolution with your matrix multiplication, as I see it, but I’m not yet convinced that the approximation is good.) I say that the “natural” initialization is to put all of the probability mass on zero in  which is to say that
which is to say that  should be equal to
should be equal to 
Hi Tom,
I’ll be glad to look at it when you post. Thanks for going through the code. That is why I made it public; I would like it to be as good as possible, and verifiable by everyone.
Bill Basener:
Nobody will take issue with this statement, I think. For example, in conservation biology the increased genetic risk for extinction of small populations is well known. What is puzzling is the fact that a population of a billion individuals does not come close to my idea of a small population. So something about your model is not “biologically plausible” and the most obvious candidate would be the mutation rate (set at one mutation per individual per generation). Would you say that the influx of deleterious mutations is exaggerated for the purpose of demonstrating that fitness can go down in your model or is this deleterious mutation rate also biologically plausible?
ETA: corrected omission
Another thing that strikes is me is that, although the population is finite, there is no genetic drift (Tom English already alluded to that particular quirk). Now an obvious effect of drift would be the immediate loss of a fair share of the newly introduced mutations (which I believe does not happen in this model), effectively reducing the influx of deleterious mutations. Normally, genetic drift would also counteract the efficacy of natural selection, but there is no viability selection going on in this particular model so I have no clue how this will play out.
Large populations creates another set of problems not modeled well by fisher’s theorem, but the time of fixation of beneficials (like say astronomically long times to fixation). But the mutational load problem is there since deleterious mutations don’t have to fix in a population to damage it.
What good is an improved kidney (beneficial) when 100 defects (deleterious change to heart, eyes, pancrease, liver, etc.) come with it? Even a 10 deleterious to 1 beneficial ratio doesn’t look very promising if the ABSOLUTE count of deleterious mutations per individual per generation exceeds Muller’s limit (about 1 per generation per individual).
So…what you seem to be saying is that even Darwinian speculations don’t work out? How could the real experiments do then?
I think that the best way to prove who is right and who is wrong is to experimentally test them, don’t you think?
How could we design such an experiment and what organism should we test?
How about fruit fly? Or make some plants to turn into mobile organisms or something? Could we design a fruit fly experiment to make it evolve into something else? We got all the evidence from Harshman nested hierarchies, don’t we?
Lets do some experiments according to the genetic evolutionary path, and let’s prove the Darwinian speculations to be true. How difficult could it be to follow the sequence of events that natural, dumb processes did?
I believe this is offset by the higher number of benificial mutations in large populations.
Yes, a high enough deleterious mutation rate will swamp populations of any size. However, if this rate is not so high, purifying selection can keep deleterious mutations rare in the population. And as it happens, strongly deleterious mutations are rare in the human population.
Let’s do chickens. Do you have time to chase some up a tree any time soon?
I realize others have said all I am about to say, but I want to see if I can put all my objections and suspicions into a fairly short form. Translation—I want to vent.
I am only a dilettante, but this seems like a tempest in a teapot on the merits, just another math model showing mutational meltdown, something you already see discussed in textbooks. My next comment belongs after the other post, but I don’t want to post twice, so here it is—Fisher’s fundamental theorem is treated as something not terribly important in population genetics texts that I have seen. Maynard Smith is dismissive, and Sean Rice has a page or two referencing Price and Felsenstein’s own book is much the same. The two authors are obviously trying to puff up the importance of their own work by making it seem like they are overturning a central pillar of the subject. This will work on the creationist audience.
Second, the model may be new, but the concept is not. It can all be stated in words fairly simply—if a population of organisms is near a fitness optimum then most mutations will be harmful and if the mutation rate is too great, stabilizing selection will not be able to prevent the population from going extinct. As a mere dilettante I have seen this discussed numerous times over the years both in the standard texts and in books and papers and articles about the origin of sex. The assumption is that most organisms are near some local optimum so nearly all mutations are either neutral or harmful and then the question is why they still exist. That question should be asked here. If this model is biologically realistic, then does this mean all organisms should be extinct already?On the other hand if a population is not near an optimum, presumably because of an environmental change, then there may be some beneficial mutations or variation already in the population and Fisher’s theorem might be applicable in that additive variance about the fitness mean will be used to drive the fitness level up.
Creationists usually say they accept micro evolution and don’t have a problem with the observations in the field or in the laboratory which demonstrate it, but this work will be presented by creationists as showing that the standard theory of how natural selection and random variation drive evolution is fundamentally flawed. The authors are reasonable here, but I am cynical enough to think that the intended audience in the creationist community will be told that we now know that natural selection can’t possibly win the battle against mutational meltdown, let alone produce new adaptations. If they are busy telling the creationists that their work is nothing fundamentally new and can’t be used to disprove micro evolution, then that would be a testament to their good faith, but it would also cut the ground out from under all the creationist excitement.
I did a bit of googling and there is a fair amount of work in this area. Some of it focuses on the rate of evolution in large populations where there is likely to be a significant number of beneficial mutations.
http://www.pnas.org/content/109/13/4950
On skimming this and one other article from 2007,, this isn’t just modeling of hypothetical populations and beneficial mutations that only occur in the imaginations of evolutionary theorists. They seem to think there is actual experimental support for their models.
And here is a piece on Lenski’s pet bacteria.
https://www.ncbi.nlm.nih.gov/pubmed/27479321
So evolution with the accumulation of beneficial mutations is something people observe in the lab.
Thing is, unless I am mistaken the authors think that only 2018+4004 years are available in the past, and the issue in their minds is whether this shows that The End Is Nigh.
Thing is, unless I am mistaken you and the others can do your speculative science only with the assumptions that genes already exist because they appeared somehow…
Whether 2018+4004 years are available in the past or 2018+400400000000000000…
Genes that don’t exist can’t be mutated or eliminated…until they actually come into existence…
Your mocking them doesn’t give your unfounded assumptions any credibility just because you blindly chose to believe it…
Let’s listen to excuses now how population genetics assumes how sheer dumb luck did it by designing natural processes… 😉
Take it away Joe!
But, genes do exist. This is uncontroversial, right?
And with enough mutations, a gene can turn into a different one.
Done.
Joe—well, that makes sense if they are young earthers, but in that case the old earth creationists should be questioning their paper too.
This is a testable hypothesis. If fitness is declining, especially in the human genome, this is a testable hypothesis. Although this depends on one’s definition of fitness.
I don’t know of a single geneticist of any repute who thinks the human genome is improving. And that includes Michael Lynch.
If you’re talking about population-level fitness, isn’t your claim falsified by the rapidly expanding human population? According to your chosen parameters, shouldn’t it require thousands of offspring per person just in order to sustain the current population size?
No, it just shows the absurdity of the population-level fitness definition and the ability of changing technology to mask the effects of heritable diseases. We probably have a higher proportion of people with juvenile diabetes and other severe maladies than at any other time. You want to argue the collective human genome is more fit than our ancestors? Ok, but people with the medical notion of “fit” would understandably have a different view.
Even if the average human today has a comparatively lower reproductive fitness in our ancestral environment, compared to our ancestors, that still doesn’t mean humanity, the diversity of life in general, or the Earth is young. Nor that species could not have evolved. Nor does it mean Jesus is coming back.
I see you snipped out the most relevant portion of my comment. Inadvertently, I assume. Deleterious mutations on the scale you’re contemplating would have far greater and more immediate effects than are observed.
Ok, I’ll try again. It seems to me Bill and John’s simulation pertain to fixed S-coefficients. Take the situation of those with juvenile diabetes and those without. In prior generations without insulin treatments like we have now, the S-coefficient (relative fitness) of juvenile diabetes was extremely deleterious, practically fatal as far as I know. In the modern day, and with expanding populations, the deleterious S-coefficient of juvenile diabetes traits, is less deleterious. Add to that fact the absolute fitness of all traits is going up
wA = 1/2 vA fA
wA = absolute fitness
vA = viability
fA = fecundity
It seems viability has gone up substantially to swamp lower fecundity (due to probably birth control or whatever). But bottom line, there’s a lot of information erased in simplistic models.
So is Bill and John’s work falsified? Problematic is how to apply it situations like what I’m describing. I do think the point they’ve made, that Fisher’s theorem needs correction is valid.
However, inadverdently or not, I think their revision arrives at the right conclusion which is independently verifiable by the “bonkers” derivation that relates to Muller’s limit. We’ll see.
Michael Lynch:
http://www.pnas.org/content/107/3/961.full
So at best, the argument is over what is the correct inference to the conclusion, not the actual conclusion itself, which is reduced fitness over the next few centuries in the human genome.
Ah, but the conclusion you’re working toward isn’t in the future; it’s in the past. If the implied rate of deleterious mutation had been happening for, say, the last 6,000 years, shouldn’t we be extinct by now?
So the genetic load has actually decreased during the last centuries?
That’s beyond the scope of this discussion and this paper.
I don’t know. I’ll let the specialists take that one on. It’s a good question.
I believe the term is “mutational load” not “genetic load”. I think since fecundity went down, the mutational load actually went up. I could be wrong about that however.
Of course it is.
Mutational load is the part of the genetic load that is caused by recurrent deleterious mutation.
Fecundity went down mainly because of birth control, not because of the accumulation of deleterious variants. As you observed yourself, the impact of deleterious variants has decreased substantially in our times. This has decreased the mutational load (and thus, also the genetic load).
So the “substantial reduction in human fitness” that Michael Lynch forecasts represents the return to the mutation-selection equilibrium that we had before the increase in health care and standard of living of the recent past. It is expected to stop once we reach that equilibrium again (or better yet: found a another way to deal with heritable diseases).
As we all know by now, ID is science, not religion. It’s the kind of science that brings together, under one ginormous tent, hosts of lawyers, philosophers, mathematicians, and engineers (plus several biologists) who agree to disagree on the question of whether life has been evolving for thousands of years or for billions of years. Three trailing zeros or nine trailing zeros — it doesn’t really matter.
What are you implying? This is the sort of high-fidelity mathematical precision that is so characteristic of ID.
They do? Genes exist and that is your answer?
So do cars? What processes made them ?
If I put all the individual car parts next to the ocean vents, would they assemble them into a car?
How about all the nucleotides? If I put them next the creative ocean vents, will they become genes? Yeah, if you are delusional…
But even scientific delusion doesn’t make it to become a true scientific evidence even if you want it to be so…
Meds are available but many psychotic patients don’t what to take them…
Do you know why? Because they like their delusion much more than reality…
The question is : Do you?
Looks like Tom pricked his quantum brain when he inserted the earing into his ear. Challenging religion doesn’t work when your own beliefs are religious… Calling your beliefs scientific doesn’t cut it unless you have proof, does it?
Otherwise it is a wishful thinking of a hopeful being, isn’t it?
This confuses me. I can understand that the further from optimal a population is (for its environmental role), the more likely any mutation is to be helpful — and so conversely, a population sitting square at (a local) optimum can ONLY suffer deleterious or neutral mutations. Accordingly, this population wanders afield from the optimum.
But my problem is, as this process continues, the ratio of beneficial mutations can only rise. So we would seem to have a negative feedback process in operation, with beneficial mutations warring with deleterious mutations, resulting generally in a stalemate, an equilibrium short of fully optimal and staying there.
Moving right along, environments themselves change over time. My very limited reading suggests that populations do not “chase” a changing environment, but rather branch off a more suitable species or two, then go extinct. I wonder if this observed stubborn persistence of species in the face of environmental change (so they’re more likely to go extinct than adapt) is reflected in any of these models.
Arguing about the fitness of the human population seems beside the point. Our situation is a special case because of medical and sanitation advances. There are millions of other species and if the deleterious mutation rate is so overwhelmingly powerful then the end should be nigh for everything. Some species should be going extinct because of this problem all by themselves. Lenski’s bacteria should not have evolved greater fitness, etc…
Tom English— The puzzling thing to me about some of my fellow Christians ( I am one) is that some of the ID crowd are honest about the evidence regarding the age of the earth, but most of the theological problems the creationists have are already present when you grant that. And there is even a young earther ( I forgot his name) whose blog I used to visit who was totally upfront about the fact that the case for evolution is actually pretty strong. He rejects it on faith, hoping to find good scientific evidence at some point.
You are probably talking about Todd Wood.
Lizzie had a soft spot for him. He’s on the blog roll. I see he’s still blogging and still a committed Creationist. His post on dealing with school shootings is a bit… well, read it and wonder.