The Search Problem of William Dembski, Winston Ewert, and Robert Marks

Posted on January 29, 2018 by DiEb

Introduction to Evolutionary Informatics, by Robert J. Marks II, the “Charles Darwin of Intelligent Design”; William A. Dembski, the “Isaac Newton of Information Theory”; and Winston Ewert, the “Charles Ingram of Active Information.” World Scientific, 332 pages.

Classification: Engineering mathematics. Engineering analysis. (TA347)
Subjects: Evolutionary computation. Information technology–Mathematics.¹

Search is a central term in the work of Dr. Dr. William Dembski jr, Dr. Winston Ewert, and Dr. Robert Marks II (DEM): it appears in the title of a couple of papers written by at least two of the authors, and it is mentioned hundreds of times in their textbook “Introduction to Evolutionary Informatics“. Strangely – and in difference from the other central term information, it is not defined in this textbook, and neither is search problem or search algorithm. Luckily, dozens of examples of searches are given. I took a closer look to find out what DEM see as the search problem in the “Introduction to Evolutionary Informatics” and how their model differs from those used by other mathematicians and scientists.

A Smörgåsbord of Search Algorithms

In their chapter 3.8 “A Smörgåsbord of Search Algorithms“, DEM present

Table 3.2. A list of some search algorithms.

active set method³⁸
adaptive coordinate descent³⁹
alpha–beta pruning⁴⁰
ant colony optimization⁴¹
artificial immune system optimization⁴²
auction algorithm⁴³
Berndt–Hall–Hall–Hausman algorithm⁴⁴
blind search
branch and bound⁴⁵
branch and cut⁴⁶
branch and price⁴⁷
Broyden–Fletcher–Goldfarb–Shanno (BFGS) method⁴⁸
Constrained optimization by linear approximation (COBYLA)⁴⁹
conjugate gradient method⁵⁰
CMA-ES (covariance matrix adaptation evolution strategy)⁵¹
criss-cross algorith ⁵²
cross-entropy optimization⁵³
cuckoo search⁵⁴
Davidon’s variable metric method⁵⁵
differential evolution⁵⁶
eagle strategy⁵⁷
evolutionary programs⁵⁸
evolutionary strategies
exhaustive search
Fibonacci search^59,60
firefly algorithm⁶¹
Fletcher–Powell method ⁶²
genetic algorithms⁶³

glowworm swarm optimization⁶⁴
golden section search^65,66
gradient descent⁶⁷
great deluge algorithm⁶⁸
harmony search⁶⁹
imperialist competitive algorithm⁷⁰
intelligent water drop optimization⁷¹
Karmarkar’s algorithm⁷²
Levenberg–Marquardt algorithm⁷³
Linear, Quadratic, Integer and Convex Programming⁷⁴
Nelder–Mead method⁷⁵
Newton–Raphson method⁷⁶
one-at-a-time search⁷⁷
particle swarm optimization⁷⁸
pattern search⁷⁹
POCS (alternating projections onto convex sets) ⁸⁰
razor search⁸¹
Rosenbrock methods ⁸²
sequential unconstrained minimization technique (SUMT)⁸³
shuffled frog-leaping algorithm⁸⁴
simplex methods⁸⁵
simulated annealing⁸⁶
social cognitive optimization⁸⁷
stochastic gradient search⁸⁸
stochastic hill climbing⁸⁹
Tabu search⁹⁰
Tree search⁹¹
Zionts–Wallenius method⁹²

A smörgåsbord indeed – and for me it is absolutely not clear how this list was constructed: DEM just write “[a]n incomplete list of search algorithms³⁷ is provided in Table 3.2.” and give as a footnote Donald Knuth’s third volume of the “Art of Computing Programming: Sorting and Searching”. But obviously, this list is not taken from the book, as

Knuth definition of a search covers only a finite search-space:

“In general, we shall suppose that a set of N records has been stored, and the problem is to locate the appropriate one. As in the case of sorting, we assume that each record includes a special field called its key.”
some of the methods were developed after 1973, the year Knuth’s book was published according to DEM

I assume it never hurts to mention Donald Knuth. Fortunately, the footnotes in the table (which is listed at the end of the chapter) are a little bit more to the point. To save jumping back and forth, I added the given source to every item in the list in a second column. I looked up some of them and I tried to find out which kind of sort problem the authors of the paper have in mind – this, I put into the third column².

method	source	search problem
active set method	J. Nocedal and S. Wright, Numerical Optimization (Springer Science & Business Media, 2006).	optimization problem: 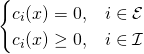$\min_{x \in \mathbb{R}^n}f(x)$ subject to $\begin{cases}c_i(x) = 0, &i \in \mathcal{E}\\c_i(x) \ge 0,& i \in \mathcal{I} \end{cases}$
adaptive coordinate descent	I. Loshchilov, M. Schoenauer, and M. Sebag, “Adaptive Coordinate Descent.” In Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation (ACM, 2011), pp. 885–892.	(separable) continuous optimization problems
alpha–beta pruning	Donald E. Knuth and Ronald W. Moore, “An analysis of alpha-beta pruning.” Artif Intel, 6(4), pp. 293–326 (1976).	“searching a large tree of potential continuations” (p. 234)
ant colony optimization	M. Dorigo, V. Maniezzo, and A. Colorni, “Ant system: optimization by a colony of cooperating agents.” IEEE Transactions on Systems, Man, and Cybernetics — Part B, 26(1), pp. 29–41 (1996).	stochastic combinatorial optimization (here)
artificial immune system optimization	Leandro N. de Castro and J. Timmis, Artificial Immune Systems: A New Computational Intelligence Approach (Springer, 2002), pp. 57– 58.
auction algorithm	Dimitri P. Bertsekas, “A distributed asynchronous relaxation algorithm for the assignment problem.” Proceedings of the IEEE International Conference on Decision and Control, pp. 1703–1704 (1985).
Berndt–Hall–Hall–Hausman algorithm	Ernst R. Berndt, Bronwyn H. Hall, Robert E. Hall, and Jerry A. Hausman, “Estimation and inference in nonlinear structural models.” Annals of Economic and Social Measurement, 3(4), pp. 653–665 (1974).	non-linear least squares problems
blind search
branch and bound	Patrenahalli M. Narendra and K. Fukunaga, “A branch and bound algorithm for feature subset selection.” IEEE Transactions on Computers, 100(9), pp. 917–922 (1977).
branch and cut	M. Padberg and G. Rinaldi, “A branch-and-cut algorithm for the resolution of large-scale symmetric traveling salesman problems.” SIAM Rev, 33(1), pp. 60–100 (1991).
branch and price	Cynthia Barnhart, Ellis L. Johnson, George L, Nemhauser, Martin W.P. Savelsbergh, and Pamela H. Vance, “Branch-and-price: Column generation for solving huge integer programs.” Operations Research, 46(3), pp. 316–329 (1998).
Broyden–Fletcher–Goldfarb–Shanno (BFGS) method	J. Nocedal and Stephen J. Wright, Numerical Optimization, 2nd edition (Springer-Verlag, Berlin, New York, 2006).
Constrained optimization by linear approximation (COBYLA)	Thomas A. Feo and Mauricio G.C. Resende, “A probabilistic heuristic for a computationally difficult set covering problem.” Op Res Lett, 8(2), pp. 67–71 (1989).
conjugate gradient method	A.V. Knyazev and I. Lashuk, “Steepest descent and conjugate gradient methods with variable preconditioning.” SIAM J Matrix Anal Appl, 29(4), pp. 1267–1280 (2007).	linear system with a real symmetric positive definite matrix of coefficients A
CMA-ES (covariance matrix adaptation evolution strategy)	Y. Akimoto, Y. Nagata, I. Ono, and S. Kobayashi. “Bidirectional relation between CMA evolution strategies and natural evolution strategies.” Parallel Problem Solving from Nature, PPSN XI, pp. 154–163 (Springer, Berlin Heidelberg, 2010).
criss-cross algorithm	Dick den Hertog, C. Roos, and T. Terlaky, “The linear complimentarity problem, sufficient matrices, and the criss-cross method.” Linear Algebra Appl, 187, pp. 1–14 (1993).
cross-entropy optimization	R.Y. Rubinstein, “Optimization of computer simulation models with rare events.” Eur J Ops Res, 99, pp. 89–112 (1997). R.Y. Rubinstein and D.P. Kroese, The Cross-Entropy Method: A Unified Approach to Combinatorial Optimization, Monte-Carlo Simulation, and Machine Learning (Springer-Verlag, New York, 2004).	given a set $\mathcal{X}$ , and an $\mathbb{R}-$ valued function on $\mathcal{X}$ , determine $\max_{\textbf{x} \in \mathcal{X}} S(\textbf{x})$ (here p.4)
cuckoo search	X.S. Yang and S. Deb, “Cuckoo search via Lévy flights.” World Congress on Nature & Biologically Inspired Computing (NaBIC 2009). IEEE Publications, pp. 210–214. arXiv:1003.1594v1.
Davidon’s variable metric method	W. C. Davidon, “Variable metric method for minimization.” AEC Research Development Rept. ANL-5990 (Rev.) (1959).
differential evolution	P. Rocca, G. Oliveri, and A. Massa, “Differential evolution as applied to electromagnetics.” Antennas and Propagation Magazine, IEEE, 53(1), pp. 38–49 (2011).
eagle strategy	Xin-She Yang and Suash Deb, “Eagle strategy using Lévy walk and firefly algorithms for stochastic optimization.” Nature Inspired Cooperative Strategies for Optimization (NICSO 2010) (Springer Berlin Heidelberg, 2010), pp. 101–111.
evolutionary programs	Jacek M. Zurada, R.J. Marks II and C.J. Robinson; Editors, Computational Intelligence: Imitating Life (IEEE Press, 1994). M. Palaniswami, Y. Attikiouzel, Robert J. Marks II, D. Fogel, and T. Fukuda; Editors, Computational Intelligence: A Dynamic System Perspective (IEEE Press, 1995).
evolutionary strategies
exhaustive search
Fibonacci search	David E. Ferguson, “Fibonaccian searching.” Communications of the ACM, 3(12), p. 648 (1960). J. Kiefer, “Sequential minimax search for a maximum.” Proceedings of the American Mathematical Society, 4(3), pp. 502–506 (1953).
firefly algorithm	Xin-She Yang, “Firefly algorithms for multimodal optimization.” In Stochastic Algorithms: Foundations and Applications (Springer Berlin Heidelberg, 2009), pp. 169–178.
Fletcher–Powell method	R. Fletcher and M.J.D. Powell, “A rapidly convergent descent method for minimization.” Computer J. (6), pp. 163–168 (1963).
genetic algorithms	David E. Goldberg, Genetic Algorithms in Search Optimization and Machine Learning (Addison Wesley, 1989). R. Reed and R.J. Marks II, “Genetic Algorithms and Neural Networks: An Introduction.” Northcon/92 Conference Record (Western Periodicals Co., Ventura, CA, Seattle WA, October 19–21, 1992), pp. 293–301.
glowworm swarm optimization	K.N. Krishnanand and D. Ghose. “Detection of multiple source locations using a glowworm metaphor with applications to collective robotics.” Proceedings of the 2005 IEEE Swarm Intelligence Symposium (SIS 2005), pp. 84–91 (2005).
golden section search	A. Mordecai and Douglass J. Wilde. “Optimality proof for the symmetric Fibonacci search technique.” Fibonacci Quarterly, 4, pp. 265–269 (1966). A. Mordecai and Douglass J. Wilde. “Optimality proof for the symmetric Fibonacci search technique.” Fibonacci Quarterly, 4, pp. 265–269 (1966).
gradient descent	Jan A. Snyman, Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms (Springer Publishing, 2005).	constrained optimization problem 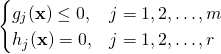$minimize_{w.r.t. \mathbf{x}}f(\mathbf{x})$ , $\mathbf{x} = [x_1, x_2,\ldots, x_n]^T \in \mathbb{R}^n$ subject to $\begin{cases}g_j(\mathbf{x}) \le 0, & j=1,2, \ldots, m \\ h_j(\mathbf{x})=0,& j=1,2,\ldots,r\end{cases}$
great deluge algorithm	Gunter Dueck, “New optimization heuristics: the great deluge algorithm and the record-to-record travel.” J Comp Phys, 104(1), pp. 86–92 (1993).
harmony search	Zong Woo Geem, “Novel derivative of harmony search algorithm for discrete design variables.” Applied Mathematics and Computation, 199, (1), pp. 223–230 (2008).
imperialist competitive algorithm	Esmaeil Atashpaz-Gargari and Caro Lucas, “Imperialist competitive algorithm: an algorithm for optimization inspired by imperialistic competition.” 2007 IEEE Congress on Evolutionary Computation (CEC 2007), pp. 4661– 4667 (2007).
intelligent water drop optimization	Shah-Hosseini Hamed, “The intelligent water drops algorithm: a natureinspired swarm-based optimization algorithm.” Int J Bio-Inspired Comp, 1(1/2), pp. 71–79 (2009).
Karmarkar’s algorithm	Karmarkar Narendra, “A new polynomial-time algorithm for linear programming.” Proceedings of the Sixteenth Annual ACM Symposium on Theory of Computing, pp. 302–311 (1984).
Levenberg–Marquardt algorithm	Kenneth Levenberg, “A Method for the Solution of Certain Non-Linear Problems in Least Squares.” Quart App Math, 2, pp. 164–168 (1944).
Linear, Quadratic, Integer and Convex Programming	Alexander Schrijver, Theory of Linear and Integer Programming (John Wiley & Sons, 1998). Yurii Nesterov, Arkadii Nemirovskii, and Yinyu Ye, “Interior-point polynomial algorithms in convex programming.” Vol. 13. Philadelphia Society for Industrial and Applied Mathematics (1994).	given a subset $\Pi \subset \Sigma^* \times \Sigma^$ , where $\Sigma$ is some alphabet, then the search problem is: given string $z \in \Sigma^$ , find a string $y$ such that $(z,y) \in \Pi$ , or decide that no such string $y$ exists.
Nelder–Mead method	K.I.M. McKinnon, “Convergence of the Nelder–Mead simplex method to a non-stationary point.” SIAM J Optimization, 9, pp. 148–158 (1999).
Newton–Raphson method	E. Süli and D. Mayers, An Introduction to Numerical Analysis (Cambridge University Press, 2003).
one-at-a-time search	A.H. Boas, “Modern mathematical tools for optimization,” Chem Engrg (1962).
particle swarm optimization	J. Kennedy and R. Eberhart, “Particle Swarm Optimization.” Proceedings of IEEE International Conference on Neural Networks IV, pp. 1942–1948 (1995).
pattern search	A. W. Dickinson, “Nonlinear optimization: Some procedures and examples.” Proceedings of the 19th ACM National Conference (ACM, 1964), pp. 51–201.
POCS (alternating projections onto convex sets)	Robert J. Marks II, Handbook of Fourier Analysis & its Applications (Oxford University Press, 2009).
razor search	J.W. Bandler and P.A. Macdonsdd, “Optimization of microwave networks by razor search.” IEEE Trans. Microwave Theory Tech., 17(8), pp. 552–562 (1969).
Rosenbrock methods	H.H. Rosenbrock, “An automatic method for finding the greatest or least value of a function.” Comp. J., 3, pp. 175–184 (1960).
sequential unconstrained minimization
technique (SUMT)	John W. Bandler, “Optimization methods for computer-aided design.” IEEE Transactions on Microwave Theory and Techniques, 17(8), pp. 533–552 (1969).
shuffled frog-leaping algorithm	Muzaffar Eusuff, Kevin Lansey, and Fayzul Pasha, “Shuffled frog-leaping algorithm: a memetic meta-heuristic for discrete optimization.” Engineering Optimization, 38(2), pp. 129–154 (2006).
simplex methods	M.J. Box, “A new method of constrained optimization and a comparison with other methods.” Computer J., (8), pp. 42–52 (1965). J.A. Nelder and R. Mead, “A simplex method for function minimization.” Computer J., 7, pp. 308–313 (1965).
simulated annealing	S. Kirkpatrick, C.D. Gelatt, and M.P. Vecchi, “Optimization by simulated annealing.” Science, 220(4598), pp. 671–680 (1983).
social cognitive optimization	X.-F. Xie, W. Zhang, and Z. Yang, “Social cognitive optimization for nonlinear programming problems.” Proceedings of the First International Conference on Machine Learning and Cybernetics, 2, pp. 779–783 (Beijing, 2002).
stochastic gradient search	James C. Spall, Introduction to Stochastic Search and Optimization (2003).	Find the value(s) of a vector $\mathbf{\theta} \in \Theta$ that minimize a scalar-valued $loss function$ $L(\mathbf{\theta})$ or: Find the value(s) of $\mathbf{\theta} \in \Theta$ that solve the equation $\mathbf{g}(\mathbf{\theta}) = \mathbf{0}$ for some vector-valued function $\mathbf{g}(\mathbf{\theta})$
stochastic hill climbing	Brian P. Gerkey, Sebastian Thrun, and Geoff Gordon, “Parallel stochastic hillclimbing with small teams.” Multi-Robot Systems. From Swarms to Intelligent Automata, Volume III, pp. 65–77. (Springer Netherlands, 2005).
Tabu search	F. Glover, “Tabu Search — Part I.” ORSA J Comput, 1(3), pp. 190–206 (1989). “Tabu Search — Part II”, ORSA J Comput, 2(1), pp. 4–32 (1990).
Tree search	Athanasios K. Sakalidis, “AVL-Trees for Localized Search.” Inform Control, 67, pp. 173–194 (1985). R. Seidel and C.R. Aragon, “Randomized search trees.” Algorithmica, 16(4–5), pp. 464–497 (1996).
Zionts–Wallenius method	S. Zionts and J. Wallenius, “An interactive programming method for solving the multiple criteria problem.” Manage Sci, 22(6), pp. 652–663 (1976).

Often the quoted texts are scientific papers: those expect their readers to be accustomed to the general framework of their specific problems, and will not define the term “search problem” from scratch. Instead, they will just mention the specific problem which they tackle – like statistical combinatorial optimization.

But there are some textbooks, too: I tried to look them up and to quote what the authors of those define as their search problem. Nocedil and Snyman both describe the classical optimization problem: here, the search space is a subset of an $n$ -dimensional vector space $V$ over $\mathbf{R}$ – as $V$ is restricted by some (in)equations. Finding the target means minimizing an $R$ -valued function on this set.

On the other hand, Macready and Wolpert – in their classical paper “No Free lunch Theorems for Optimization“¹ – look at two finite sets $\mathcal{X}$ and a sortable $\mathcal{Y}$ and wish to minimize a function $f: \mathcal{X} \rightarrow \mathcal{Y}$ by finding the $x \in \mathcal{X}$ such that $f(x)$ is minimal.

What have all these approaches in common? A set to search on and a function which can be optimized. In most cases, the range of the function is $\mathbb{R}$ , $\mathbb{Z}$ , or $\mathbb{N}_0$ , but for some problems (as mentioned in section 3.7.2. Pareto optimization and optimal sub-optimality of Introduction into Evolutionary Informatics), another partially ordered set will be used. I will ignore this for the time and just choose an ordered set for my definition of a optimization problem which should cover virtually all the cases discussed above:

General Optimization Problem

given:

a set $\Omega$

an ordered set $\mathcal{Y}$ and

a function $f: \Omega \rightarrow \mathcal{Y}$

find $x \in \Omega$ such that $f(x) = \min f$

As said before, optimizing and searching are virtually the same, but to stress the character of a search I introduce a target – something, which is mentioned in all the searches of DEM. So, my search problem is:

General Search Problem

given:

a set $\Omega$

an ordered set $\mathcal{Y}$

a target $T \subset \Omega$ and

a function $f: \Omega \rightarrow \mathcal{Y}$ such that $T = \{\tau \in \Omega | f(\tau)=\min f \}$

find $x \in T$

Nothing substantial has changed, the definition just became a little more verbose. I am quite sure that most authors of the papers on the table would accept this as a good attempt of a definition – but is it the search problem which DEM have in mind?

On page 48, they provide an example of a search credited to Walter Bradley:

Kirk is an armadillo foraging for grubs when he is bitten by a spider that makes him blind. Kirk wants to return to his armadillo hole, but is disoriented. He knows, though, that his hole is at the lowest elevation in the immediate area, so he balls up and rolls downhill to his hole. When Kirk does this, he is not explicitly seeking his hole. His surroundings are fortuitously designed to take him there. Kirk’s target is thus implicit in the sense it is not specifically sought, but is a result of the environment’s action on him. He can bounce off of trees and be kicked around by playful kids. And repeated trials of rolling down the hill might take drastically different paths. But ultimately, Kirk will end up in his hole at the bottom of the hill. Kirk reaches his home because of information he acquires from his environment. The environment must be designed correctly for this to happen.

Here, $\Omega$ is Kirk’s habitat, $f$ is given as the elevation. What is surprising is that DEM make a distinction between the minimum of the function $f$ and Kirk’s intended target $T$ , his borrow hole. Luckily, both coincide, but DEM imply that this is not necessarily the case!

Next, they revisit their “pancake search example”: here, the taste of the pancake as a function depends smoothly on a variety of factors like amount of ingredients, oven temperature, baking time, etc. – the possible combinations of which make up $\Omega$ . On this $\Omega$ , a cook looks for the best taste by optimizing the taste function. Now, they restrict $\Omega$ by additional conditions to $\Omega'$ , such that the original extreme of $f$ does not lie in the new restricted set.

For the definitions of optimization/search problem above, this does not pose a problem: there is now the set $\Omega'$ to search on, looking for the optimum of $f|_{\Omega'}$ . Though the new solution will taste worse than the original one, the new target is the solution of the new restricted problem.

Not so for DEM: “If, however, the environment is constrained in a negative way, the target may never be found even if it was available prior to the alteration.”

That is the great difference between the problems which all other scientists discuss and the ones of DEM: DEM have decoupled the optimum of the function and the target, arriving quite another version of a search problem:

DEM’s Search Problem

given:

a set $\Omega$

an ordered set $\mathcal{Y}$

a target $T \subset \Omega$ and

a function $f: \Omega \rightarrow \mathcal{Y}$

find $x \in T$

The Problems with DEM’s Search Problem

First there is of course the problem of applicability: it is not clear how any of DEM’s results is relevant for the problems in the table as those concern fundamentally different problems.

Then there is a problem of procedure: for an algorithm for a search or optimization, generally some information about $\Omega$ is given and (a finite number of) values of $f$ can be obtained. If $T$ is independent of $f$ , how is it ever possible to say that a target was hit? This additional information can only be given ex cathedra afterwards!

Not every one of the search algorithms stated in the table will always identify the target, but in many cases, this is possible – at least theoretically: if possible, an exhaustive search will always give you the target. Not so for DEM: even if you have calculated $f$ for all elements of $\Omega$ and found the optimum, this does not have to be the intended target which still has to be revealed.

Why do DEM use their definition?

I would like to answer this question using Dawkins’s weasel. Then

$\Omega$ is the set of strings consisting from 28 letters chosen from the alphabet ABCDEFGHIJKLMNOPQRZ plus * as a sign indicating a space
$T=$ METHINKS*IT*IS*LIKE*A*WEASEL
$f$ is given by the number of correct letters – a number from 0 to 28.

Imagine someone has programmed an algorithm using $f$ which will find the target in 100% of all runs. The big question: How will it fare for the target string I*REALLY*DO*NOT*LIKE*WEASELS?

My answer would be fantastic: if I*REALLY*DO*NOT*LIKE*WEASELS is the target, then it is the optimum of $f$ , so $f$ for finding this phrase is the number of common letters with I*REALLY*DO*NOT*LIKE*WEASELS…
DEM’s answer would be abysmal: though the target is I*REALLY*DO*NOT*LIKE*WEASELS, $f$ still is defined as the number of common letters with METHINKS*IT*IS*LIKE*A*WEASEL. The algorithm would result in METHINKS*IT*IS*LIKE*A*WEASEL

The advantage for DEM is stated on p. 173 “We note, however, the choice of an algorithm along with its parameters and initialization imposes a probability distribution over the search space.” Indeed, it does in their case – and it will not work with my definition. This probability distribution may appear absolutely counterintuitive to any practitioner of optimization problems, but it is the basic building block for many of DEM’s most important results.

How does DEM’s search problem work for evolution?

Some interesting characters make a cameo in DEM’s textbook: not only Bob and Monica, the pirates X, Y, and Z, Melody and Maverick, but also God and Abraham. In this spirit I would like to invent a dialogue between God and Darwin’s Bulldog:

Bulldog:	“The horse is a marvellous creature: fully adapted to its niche, really, survival of the fittest at play”
God:	“Oh no, that one is a total disaster – it may function better than any other creature in its environment, but I was aiming for pink unicorns”

For short: I think that DEM’s model does not work for the usual optimization and search problems in mathematics. It is even worse as a model applied to the real world.

Perhaps these are all strawmen?

It could be that I have erected an elaborate strawman, and that the search problem which I attributed to DEM has nothing to do with their ideas. In this case, it should be easy for DEM – or their apologists – to come forward with their definition. Or perhaps – if I am right – they may just wish to explain why their model is not horrible.

^{1. Still thankful for the nice header, Tom!↩}
^{2. Obviously, the work is not completed yet. I will look up more in the future – and I will be grateful for any contribution to this project!↩}
^{3. David H. Wolpert, William G. Macready “No Free Lunch Theorems for Optimization”, IEEE Transactions on Evolutionary Computation Vol. 1, No. 1, April 1997, p. 68↩}

crossposted from my blog

edited: David $\rightarrow$ Donald

36 thoughts on “The Search Problem of William Dembski, Winston Ewert, and Robert Marks”

Joe Felsenstein on January 30, 2018 at 1:08 am said:

Donald Knuth?
DiEb on January 30, 2018 at 1:24 am said:

Joe Felsenstein:
Donald Knuth?

Thanks – what an embarrassing error!
Joe Felsenstein on January 30, 2018 at 6:23 am said:

Dieb,

Yes, their definition is weird, as it defines a target T that has no necessary relation to the function that is computed at a point in the space. So in their scheme you can descend all you want, and find the lowest point in the space, and still not be getting any closer to the target.

A search algorithm is some way of looking at points in the space and then moving to another point (or not moving) such that doing this repeatedly might bring you close to the Target. (I won’t try for a formal definition). When we evaluate such algorithms we try them on a lot of different functions $f$ and see how close to the minimum they get, or how small the final values of $f$ is.

But since DEM define the search algorithm as including the target as well, one can’t evaluate the search algorithms in this way. If we define a different function $f$ , even if we make sure that the target is the point that minimizes this function, by definition we aren’t then evaluating the same search algorithm!
Pingback: Answering DiEb: Just what is "search" in a sense relevant to ID? | Uncommon Descent
Alan Fox on January 30, 2018 at 11:46 am said:

I normally trash trackbacks but I see the above links to an OP by Kairosfocus. The argument by fishing reel is especially daunting! 😉
fifthmonarchyman on January 30, 2018 at 12:15 pm said:

Quote:

Bulldog: “The horse is a marvellous creature: fully adapted to its niche, really, survival of the fittest at play”
God: “Oh no, that one is a total disaster – it may function better than any other creature in its environment, but I was aiming for pink unicorns”

end quote:

a couple of questions

1) Can it be said that the horse a field mouse and the fungus that feeds on grass function equally well in that environment?

2) in that environment would a pink unicorn function just as well as this animal?

https://sleezybarbhorsewear.com/wp-content/uploads/2015/01/HotPinkPoodleCostume-300×280.jpg

peace
Rumraket on January 30, 2018 at 12:18 pm said:

I could make sense of almost nothing that KF dude wrote. In part because of the several different colors, fonts and sizes of text, scattered throughout and between various barely comprehensible figures and diagrams.

In an ironic way, while it is obviously concocted to look “scientific” and “technical”, it ends up looking amateurish and unprofessional with all the messy diagrams, fonts, etc.
Joe Felsenstein on January 30, 2018 at 3:42 pm said:

At least it contains the fishing reel diagram. That used to be a regular feature of most of his long posts, but it had been missing for a while. I was worried.
GlenDavidson on January 30, 2018 at 4:21 pm said:

Joe Felsenstein:
At least it contains the fishing reel diagram.That used to be a regular feature of most of his long posts, but it had been missing for a while.I was worried.

But now “Lewontin” is missing.

I’m concerned. When you’re relying on so much on a favorite fallacy, shouldn’t you exhibit that in every post?

Glen Davidson
GlenDavidson on January 30, 2018 at 4:34 pm said:

Alan Fox:
I normally trash trackbacks but I see the above links to an OP by Kairosfocus. The argument by fishing reel is especially daunting!

I love the fishing reel. Something completely unlike anything ever found in life, what with the metal, the gears, a host of parts that could only appear via intelligent leaps.

The closest life gets to a “gear” is simply some teeth on leaping legs that help to keep motion synchronized.

And life is characterized by strangely, sometimes almost bizarrely, modified ancestral parts that often develop rather inefficiently into good parts, but hardly with the efficiency that intelligence could have imparted. Why make rigid bones in wings by fusing together many separate bones that used to become articulated in terrestrial dinosaurs? Or similarly in the human coccyx, for that matter? Somehow KF always manages to ignore the telling differences between evolution-limited life and intelligently optimized designs.

Almost like agit-prop ignores crucial facts.

Glen Davidson
Joe Felsenstein on January 30, 2018 at 4:45 pm said:

GlenDavidson: Somehow KF always manages to ignore the telling differences between evolution-limited life and intelligently optimized designs.

He does ignore that the complex fishing reel “evolved” (non-biologically) from a very simple predecessor, probably a fishing line wrapped around a piece of tree branch, which may have had the near end of the line wrapped tightly around the base of a side-branch.
Acartia on January 30, 2018 at 6:20 pm said:

And now for some reel porn.

https://uncommondescent.com/wp-content/uploads/2014/11/abu_6500c3mag.gif
Tom English on January 31, 2018 at 12:27 am said:

DiEb,

A point that the mathematically uninclined will miss is that we should not have the least doubt, having studied evolutionary informatics closely for ten years, as to what Marks, Dembski, and Ewert regard as a search problem. The failing is definitely theirs, not ours.

I surmise that if they ever bother to spell out the details, as their former colleague George Montanez has, they will not say that the function $f$ is necessarily given in the problem. The main reason I say this is that their Conservation of Information Theorems posit only that there is a finite sample space $\Omega$ and a nonempty target $T \subset \Omega.$ Whatever it is that they mean by search problem, the theorems are supposed to be relevant. So I don’t believe that they can make function $f$ a part of the problem without invalidating their prior work.

In practice, the specification of the target will not list the elements (otherwise the problem would already be solved), but instead will give properties of elements of the target. One way to do that is to write something like $T = \{x \mid f(x) \geq \theta\},$ and to specify the function $f.$ In that case, a function is specified in the problem statement, but only as part of the specification of the target.

A (rare) case in which Marks et al. make sense is the search for a bent-wire antenna design (Altschuler and Linden). The crucial aspect is that the target is specified in terms of what is observed when an antenna is built according to a design, and is tested on the bench. You can see why they regard the function $f$ used by the search program as a source of expert knowledge. The function uses a simulation package to evaluate a given design. In a straightforward sense, the simulation package is a source of information on how an antenna of a given design will perform on the bench.

When there is no such separation of the entity within the computer and the entity “out there,” Marks et al. have no answer to the obvious question, “Information about what?” And they are stunningly bizarre when they say that Richard Dawkins imbued the Weasel program with a source of expert knowledge. Basically, they’ve taken something that makes sense in a small fraction of cases, and have grossly overgeneralized. As you observe, their analysis does not apply to most of the “searches” they dump on their readers. (Talk about sham scholarship!)
Robert Byers on January 31, 2018 at 3:57 am said:

My SEARCH for a important or relevant reason for this thread came up short!
You can’t do a end run around investigations by these thinkers .
Just deal with the substance!
DiEb on January 31, 2018 at 6:10 am said:

Tom English,

Tom, you certainly remember W. Dembski’s talk at Leo Kadanoff ‘ s “Computation in Science Seminar” way back in 2014. Listening to the contributions of the audience I realized there everyone assumed that W. Dembski was using the same language as they were. That lead to misconceptions.

I wrote this article for future occasions like that: I want to have a link which I can give to mathematicians with very little knowledge about DEM’s work, so that they can get aware of the discrepancies in terminology.

That is the reason that I kept the language as neutral as possible – any mathematician should draw her or his own conclusions (hopefully something between “that’s not how we do things here” and “wow, that’s bollocks”).

In the article, I did not speculate why DEM omit such basic definitions or that their “smörgåsbord of search algorithms” resembles a Gish-gallop – those who are acquainted with the tactics of the Intelligent Design proponents will have trouble to assume benign motives….
Joe Felsenstein on January 31, 2018 at 7:16 am said:

Their arguments for many different evolutionary algorithms, that information is front-loaded into all of them, is really a Gish Gallop. While they are correct for some of them (e.g., Weasel, with its target phrase), they are very wrong for others. All they show for those others is that some parameters of the algorithm have been tuned for better speed.

One where the point they make is easily seen to be invalid is the genetic algorithm for the Traveling Salesman Problem. One is given a set of points. To front-load information in, one would have to have something put in after the points were known. But the tweaking of parameters was long before, and results in the same parameter values for all sets of points. So it cannot possibly be front-loaded information about what the solution is for that set of points.

They do this for many algorithms, claiming front-loading where there can be none, because the alleged front-loading happened long before the particular problem is known to the algorithm. They leave behind the impression that they have proven front-loading in all those cases.
Joe Felsenstein on January 31, 2018 at 4:36 pm said:

Joe Felsenstein: the genetic algorithm for the Traveling Salesman Problem.

Oops, I get this wrong every time. I should have said “the genetic algorithm for the Steiner Tree Problem.” The rest of my comment does not need alteration.
GeorgeMontanez on January 31, 2018 at 6:56 pm said:

Hey DiEb, (and Tom and Joe)

Have you thought about cases where it is natural for the target set to be specified separately from the objective function in question? As Tom has already mentioned my own thesis work, it is clear that you actually want this generalization where a learner (or search algorithm) optimizes towards a target which may not be coextensive with the true target, but the learner instead works with imperfect information. For example, if you want to perform regression but your learning algorithm only has access to linear regressors, then the target you optimize towards (the best linear function) may not be the true target (the actual real-world function you’re trying to learn). This would appear to be a natural counter-argument to the main idea of the post.

Interestingly, independently of the work of DEM, I also came to the conclusion that you actually need to take into account target sets that may differ from the min or max of a function, for this very reason. Thus, in my thesis I look at the interdependence between objective functions as exploitable information resources and possible target sets. As a result, it can be shown that the expected per-query probability of a search for a target is upper-bounded by an information ratio (similar to Fano’s inequality), taking into account the predictability of the target set, the mutual information (dependence) between the target set and objective function, blind randomness, and the endogenous information of the problem. (For example, see Theorem 3 of https://arxiv.org/pdf/1609.08913.pdf). The takeaway is that if the dependence between target set and objective function is low, so is the expected per-query probability of success. In the real-world of imperfect information it is often the case that the target set has strong, but imperfect, dependence with the objective function. Therefore, the general case of allowing varying degrees of dependence (or independence) between target sets and information resources appears both necessary and fruitful.
Tom English on January 31, 2018 at 11:21 pm said:

Tom English: (Talk about sham scholarship!)

DiEb: I wrote this article for future occasions like that: I want to have a link which I can give to mathematicians with very little knowledge about DEM’s work, so that they can get aware of the discrepancies in terminology.

That is the reason that I kept the language as neutral as possible – any mathematician should draw her or his own conclusions (hopefully something between “that’s not how we do things here” and “wow, that’s bollocks”).

I wasn’t objecting to that. It occurs to me now that I used an English idiom that is uncommon in speech, and is rare in text. Talk about X! is an exclamation at X, not a command to talk about X. Did you think that I was commanding you to talk about sham scholarship?
Tom English on February 1, 2018 at 1:49 am said:

GeorgeMontanez,

Congratulations on earning your doctorate in a highly competitive program. I am inferring good things about you from the fact that the ID movement has not made propaganda of your dissertation.

I doubt that you’ll acknowledge the point, but I’ll observe anyway that you’ve not only changed the analytic framework, but also eliminated some of the defects in the work of Marks, Dembski, and Ewert that DiEb, Joe, and I have identified over the years. Apart from that, your presentation is much more rigorous and clear than is theirs.

However, your arguments are grossly overcomplicated, as are those of Marks et al. Shortly after the preprint of your paper appeared, I generalized some of your results (Famine of Forte and Conservation of Information), and came up with simple arguments for them. I started a write-up, but never finished it. I’ll tell you now that you should not have buried the applications of Markov’s inequality deep in your arguments. When you establish that the mean performance is $p$ over all alternatives, then, whatever the non-negative measure of performance, and whatever the alternatives (problem instances or problem solvers or instance/solver pairs), it follows immediately by Markov’s inequality that the proportion (or probability) of alternatives for which performance is at least $q$ is at most $p/q.$ The applications of $-\!\log(\cdot)$ belong in corollaries, not main theorems.

I’ll mention also that I think you’re wrong to characterize active information as the (negative) pointwise Kullback-Leibler divergence, because the latter requires that the “points” be blocks in a partition of the sample space. You do not restrict targets to blocks in a partition of $\Omega.$ Shannon’s mathematical theory of communication makes sense only if the events transmitted over the channel are exhaustive, mutually exclusive, and nonempty. (Much of what Shannon did was to lay out what makes sense for a theory of information in the context of communication, and to prove that his measures had the desired properties. We’ve seen nothing analogous in evolutionary informatics. We see instead that Professor Marks is reduced, of late, to sputtering that everybody calls $-\!\log p$ information.)

By the way, if Dembski and Marks did not know that a partition of the sample space was required by the measure of Kullback-Leibler divergence, then why did they posit a partition in the Horizontal No Free Lunch Theorem?
GeorgeMontanez on February 1, 2018 at 2:57 am said:

Hi Tom,

I’m interested to hear your thoughts on why it makes sense to have varying levels of dependence between target sets and objective functions (information resources). You seem to have missed my entire post, and I’d like your thoughts on it.

Thank you for your compliments and other comments. As for the Kullback-Leibler connection, the comment you reference was from a footnote in my thesis which was simply meant to relate active information to something ML researchers are already familiar with. It clearly wasn’t meant as a formal definition. (Thank you for reading my thesis, btw!) Thinking about what you wrote, if we consider the two element space partitioned by the indicator variable of success versus failure ( $1_{X \in T}$ versus $1_{X \not\in T}$ ), then we only consider those two meta-events with probabilities p and 1-p under the null distribution, and q(T,F) and 1-q(T,F) under the alternative. But I’m just thinking out loud. Although I don’t think I was even wrong in the informal case, I may be missing something.

I’d much rather hear your thoughts on the comment relevant to this thread, namely, whether searches always have to be for only maxima/minima of objective functions, or whether, like DEM, we should consider the more general case of when the target can have some imperfect degree of dependence with the information resource. I await your response to that.
Tom English on February 1, 2018 at 4:01 am said:

GeorgeMontanez: You seem to have missed my entire post, and I’d like your thoughts on it.

You know that I didn’t miss it. I went instead to issues in the backlog. I was in the middle of composing another comment when I first saw yours. I’m going to finish it, and then respond to you (tomorrow afternoon or evening, I’m guessing at this point).
Tom English on February 1, 2018 at 4:44 am said:

Tom English: The applications of $-\!\log(\cdot)$ belong in corollaries, not main theorems.

Perhaps I disagree with myself. I vaguely recall starting with a general lemma in which performance $\rho$ is a non-negative measure on $\mathcal{A} \times \mathcal{X},$ where $\mathcal{A}$ is the set of algorithms for solving a problem, and $\mathcal{X}$ is the set of all instances of the problem. Then the $-\!\log(\cdot)$ transformation would be introduced in the main theorems.

The point I’m driving at is that you should always start by deriving the most general results that you can, and then specialize them to the application of interest. It usually leads to greater insight, and often turns out to be easier than a direct assault.
DiEb on February 1, 2018 at 7:59 am said:

GeorgeMontanez,

Thank you for your comment! I will look into it a little bit closer, but here is just my first, short take: Your true target seems to be a feature of the physical world, not of the mathematical model – You modelled your real world problem using:

1) $\Omega$ as the set of linear approximations
2) $f$ as the quality of the approximation

If you are able to optimize your $f$ on $\Omega$ , you have found your solution for this search problem That this solution for the best linear model is not applicable to your original real-life problem depends on an ill-fitted model.
DiEb on February 1, 2018 at 8:02 am said:

Tom English,

Hi Tom – no sweat, my comment was just an exercise in redundancy 😉
Joe Felsenstein on February 1, 2018 at 3:45 pm said:

GeorgeMontanez,

Thanks for coming here and discussing these issues. I will hasten to say that I have not read your papers, so cannot comment on the proofs or the strategies of proof. As an evolutionary biologist, my concentration is on whether these works say something about evolution. Thus I have concentrated on the Dembski-Ewert-Marks papers and the Marks-Dembski-Ewert book. It is very clear that they claim that, in some relevant sense of “on-average”, their results show that, on average, “evolutionary searches” cannot perform better than just randomly choosing a result.

They consider a set of “searches” so broad that they include vast numbers of processes (with targets) where the process does not bias the result towards the target. They even include lots of processes that bias the result away from the target. On average over all that, the result is that one is no better off with that set of processes than with just randomly sampling a result.

In models of evolution, the results are evaluated by considering the fitnesses of the outcomes. And the processes have fitness in them, acting to bias the outcome toward genotypes with higher fitnesses. If we restrict the set of searches that we consider to those where there is that biasing, we get a very different result. Tom and I showed here that simple models of evolution are much better at increasing fitnesses than the DEM results imply.

My concern with the DEM/MDE theorems is that they are not just an abstract academic exercise in loosening the connection between the target of a search and the process of search. They are claimed to show something about the incapabilities of evolutionary processes. And I think that Tom and I have established that they show no such thing.

Your theorems are not claimed to show that evolutionary processes do horribly badly at explaining adaptation, so for now I have not spent time consideing the details of your argument, but I will be interested in following some of this thread to find out more.
GeorgeMontanez on February 1, 2018 at 9:11 pm said:

Tom,

Thank you for your initial response and I’ll wait for your comment on my original to respond further. (By missed it, I meant you didn’t seem to respond at all to what I wrote. Now I see that you were in the middle of responding, but I don’t want to get sidetracked).

DiEb,
Sometimes the true target is contained in the search space that you are optimizing on, but you only have uncertain information about it. Consider the case of some target you want to hit (say powered flight) but you have access only to an information resource imperfectly correlated with that target (say, reproductive fitness). What you’re optimizing towards may or may not get you close to your actual target. In the flight example, it makes perfect sense to ask the question “Can optimizing for reproductive success enable an algorithm to hit a target of powered flight?” Thus, it isn’t meaningless to consider a problem as specifying both an information resource and a target set, even if most people leave the target specification implicit as the min or max of the objective function. (Tom made an earlier point about making implicit things explicit, which I agree with.)

Think more about it, and I’m confident you’ll see the point. The target can have varying degrees of correspondence (or independence) with the information resource we’re optimizing against. That was my motivation for commenting, because I feel you overlooked something in your OP, something which was central to my thesis (and thus is always on my mind). Just a friendly question to think about when it may make sense to model varying degrees of dependence (as DEM do in their model as well). Hopefully I’ve given you new information to consider. I’ll leave you with the same question I asked Tom:

Do searches always have to be for only maxima/minima of objective functions, or should we also consider the more general case of when the target can have some imperfect degree of dependence with the information resource?
GeorgeMontanez on February 1, 2018 at 9:12 pm said:

Hi Joe,

Thanks for your comments. Hopefully we can all learn something from this thread. I look forward to your insights.

George
GeorgeMontanez on February 1, 2018 at 9:16 pm said:

Tom English:
The point I’m driving at is that you should always start by deriving the most general results that you can, and then specialize them to the application of interest. It usually leads to greater insight, and often turns out to be easier than a direct assault.

This is good advice. I try to do that, but am not always successful. But it is good to keep in mind and be reminded of, so thank you.
Acartia on February 3, 2018 at 3:18 pm said:

Gordon (KairosFocus) Mullings is feeling lonely over at UD. He posted one of his long obtuse OPs in response to DiEB ‘s comments on searches and search problems, and nobody is commenting. I don’t know why? It has everything a good OP should have; thousands of words with poor punctuation and no paragraph breaks, mixtures of font size and colours, plenty of irrelevant diagrams and photos with poor photoshop editing, intermeshing gears and, the clincher, an exploded view of a fishing reel.

AI, state/configuration space search and the ID search challenge
keiths on February 3, 2018 at 3:24 pm said:

All three comments so far are from him, including this one:

kairosfocus February 3, 2018 at 1:47 am

Interesting silence . . .
GlenDavidson on February 3, 2018 at 4:38 pm said:

Well, it keeps him from ranting in the streets.

As much.

Glen Davidson
GlenDavidson on February 3, 2018 at 5:11 pm said:

KF manages to fuck up a pretty simple matter, like a J-Mac or some such thing. I had written:

The closest life gets to a “gear” is simply some teeth on leaping legs that help to keep motion synchronized.

He responded:

PPS: And BTW, at least one case of a gear has been found in the world of life so one of the objectors will need to re-think the implications of design inference on gears s/he made.

What a retard. A gear is a toothed wheel, which is why I said “the closest life gets to a ‘gear’ is…” These are not gears, never mind how many bad writers call them that (including the last link), exaggerating the discovery.

He’s dumb enough to believe the propaganda, whether it’s pop science writers (so long as it fits his beliefs) or IDiots. But then he is one…

Glen Davidson
Tom English on February 6, 2018 at 7:06 pm said:

DiEb:

Were you not going to make a connection to their use of the Cracker Barrel puzzle as an example of search? What do they regard as the space $\Omega$ of possible solutions in that case? What is the target $T \subset \Omega$ ? Note that they express prior information as a preference for some moves over others. How does one make sense of that within their analytic framework? (My guess is that one does not make sense of it. The example is multifariously daft. Marks et al. did not think through the details.)

If $\Omega$ is the set of all states in which one or more of the holes is filled, and $T$ is the set of states in which exactly one of the holes is filled, then the probability of hitting the target at least once with a uniformly random sample (with replacement) of 14 states is

1-(1-15/(2^15-1))^14 = 0.00638985187.

As you know, this is greater than the probability of reaching a target state by starting with the initial state and selecting each move uniformly at random from among the moves that are valid in the current state.
Tom English on February 6, 2018 at 11:47 pm said:

Note: If the Cracker Barrel puzzle is solved by selecting a finite sequence over the set $M$ of operations (moves), as I contend, then the only straightforward designation of the search space for Marks et al. is the countably infinite set of all finite sequences of operations,

$\Omega = M^{<\mathcal{N}}.$

You cannot restrict $\Omega$ without exploiting prior knowledge of the game.

Related note: Marks et al. are wrong to place an upper bound on the length of Avida programs. The space of Avidians is countably infinite. Whether or not there happens to be an upper bound in the implementation of Avida is irrelevant. (If the upper bound were hit in an experiment with Avida, the appropriate response for the investigator would be to increase the bound, and redo the experiment.)
DiEb on February 7, 2018 at 2:30 pm said:

Tom English,

Well spotted! I have not thought about it much (and – possibly – neither did DEM …).
DEM are sampling from the set of feasible games, and I have no problem with defining $\Omega$ in such a situation as:

$\Omega = \{branches\; of\; the\; decision\; tree\},$

while $f$ is the pay-off in the sense of game theory.

It is interesting that DEM did not give us the seize of $\Omega$ – as they do for their other examples: then they would have had to explain why their beloved Bernoulli’s PrOIR works differently in this situation….