Some considerable time ago I created a toy example of fixation based on the MandM example given by Allan Miller. For various reasons that stopped working (argh, browsers!) so I’ve re-created a slightly different version.
http://mandmcounter.appspot.com/
The original OP is here: http://theskepticalzone.com/wp/?p=3877
Instead of displaying each individual MandM we see a count via a pie and line chart plus the generation each color was made extinct in.
Some of the comments/requests on the original OP are still on my to-do list with this. Currently the starting state (number of each color) is fixed in advance.
Eventually the source code will be published. If this does not work for you it would be useful to note your OS/Browser in the comments.

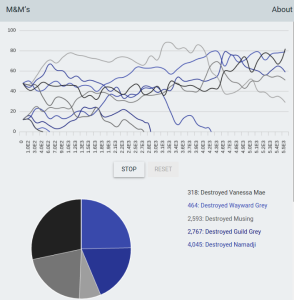
It’s behaving weird on my pc in both IE and chrome. The piechart is flashing and when the graph updates it simply redraws the entire graph on top of the previous iteration until the entire graph is just filled with criscrossing lines.
It’s OK in Chrome 41.0.2272.89 for me, and Firefox 36.0.1.
This uses something called the “ShadowDom” which is only really properly supported in browsers that don’t yet exist but in the meanwhile is emulated using “shims”. As such it may not work on older versions of current browsers – have you updated lately?
This doesn’t make sense to me. What does “of the same colour” mean? Is the second bag “randomly” distributed and “infinite” in size?
The demo runs fine on my Windows 7 Chrome.
I read that as ‘delete a random one from the first bag, then pick another from that bag. Then from the second, infinite and randomly distributed bag pick another of the same color as the one you did not eat and put them both in the first bag.’
So:
Delete 1 from the first bag. Don’t care what color it was.
Pick another 1 from the first bag – note it’s color.
Return the one you just picked to the first bag, and add another of the same color from the second infinite” bag.
Nice Job. Colour names through me off to start!
How about omitting the instruction to eat the candy. I think this causes brain fog.
You have two bags: the first is the evolving population; the second is an “infinite” supply of replacements.
1. Take one from the population bag and discard it.
2. Pick another one from the population bag and match it with one of the same color from the replacement bag.
3. Put the matching pair back in the population bag.
Thanks. We originally had all shades of grey, but….
Yes, that’s clearer. I’ll update in the next day or two.
I’m fairly dense at following instructions. I like them written at the fifth grade level.
I once wrote program installation instructions for a living. back in the DOS days, when you had to specify a drive and directory, and make sure you had enough space. Manually. I had people call and ask where the power switch was.
but where is the any key? It says “press any key”!?
It’s proof that random drift is intelligently designed.
Better would be:
1. Take one from the population bag. Send it to Joe and he will eat it.
2. Pick another one from the population bag and match it with one of the same color from the replacement bag.
3. Put the matching pair back in the population bag.
Note that it does not matter how many M&Ms are in the replacement bag, as long as it enough that there are always ones of each color when needed. As we are looking in that replacement bag for one of the right color, it does not help to describe that step as random sampling.
Great.
But when do you give the explanation of how a great great great great great great great grandmother is giving birth at the same time as a newborn infant?
Or nevermind, just use Joe’s line. If the numbers support your idea, then the analogy to biology is sound. If the numbers don’t work the way you want, well, its because the logic was flawed.
Never fails! Science without contradiction!
Phoodoo, would you be a sweetheart and answer my outstanding questions?
Some bacteria are thought to be biologically immortal (in the sense that they don’t die of old age).
A single bacterium can seed a giant population, and still mange to survive until thousands of generations later, still dividing and “giving birth” to offspring alongside it’s distant “great great great great great great great grandchildren”. So there it will sit still making copies of itself thousands of generations removed from other bacteria next to it.
Rumraket,
That will be a slight problem for your M&M theory, as the eating of the M&M is supposed to represent a death event.
Richardthughes,
“When an attempt at mathematical modeling of evolution (xxx) succeeds , it’s usually not that the math involved is wrong. It’s usually that the assumptions made were inappropriate, or that the quantities calculated do not have the biological meaning that they seem to.”
Are you going to answer my questions Phoodoo? What are you scared of?
When you answer some questions perhaps you’ll get answers to some of yours. Quid pro quo. I believe Richard has some for you…
Lol. “M&M theory”. As discussed last time round if you feel capable of giving a set of rules I’ll code them into a similar simulation. But I’m afraid simply printing “Jesus did it” won’t get either of us anywhere.
The M&M model is an implementation of the Moran Model, as I think was discussed in the earlier M&M threads. It has overlapping generations, and is the simplest model that has this. There is lots of theory that has been done on Moran Models.
A model that has discrete generations is the well-known Wright-Fisher Model. That would be implemented here by these rules:
1. Set up a new bag. Fill it with 2N M&Ms chosen in the following way:
2. Draw 2N times from the old bag.
3. Each time note the color of the M&M.
4. Draw an M&M of the same color from the supply bag.
5. Put it in the new bag. Put the M&M that was drawn from the old bag back in that bag.
This creates a new bag whose contents are drawn randomly, with replacement, from the old bag. This is one generation. The new bag now replaces the old bag, and the old bag is sent to me to have its contents eaten.
The Wright-Fisher model and the Moran Model look quite different. It can be shown that the rate of genetic drift in the Moran Model is 2x as great, per generation, as in the Wright-Fisher model.
It is also known that if we scale time so that in the Wright-Fisher model one unit of time is N generations, and in the Moran Model one unit of time is N/2 generations, and then we let N go to infinity, and we follow not the numbers of each color of M&M, but the frequencies of each color, the two processes each approach a diffusion process whose behavior is described by the Kolmogorov Forward Equation and the Kolmogorov Backward Equation. This was first worked on for two alleles (two colors) but is also true for many colors, in which case the diffusion equations are multivariate, describing diffusion on a simplex of quantities that are nonnegative and sum to 1. This was first discussed by William Feller in his great 1951 paper, for the two-allele Wright-Fisher Model.
Furthermore, if scaled this way, both processes approach the same diffusion process. So at this level of approximation they act much the same, once their differences in rate of genetic drift are taken into account. And that is done by the scaling, which reflects Sewall Wright’s concept of effective population size.
I have not explained how all this is derived, but just wanted people to know that others have already done a lot of theory on this.
I simply refuse to believe you are this stupid phoodoo. I don’t believe you’re stupid at all, so it is amazing to me you do this to yourself.
I know you don’t believe in evolution, and you don’t have to believe in evolution. You can believe whatever you want. But seriously, you don’t have to insist that everything even remotely associated with evolutionary thought is false and wrong for that reason alone.
Go back and read the rules for the simulation again and try to understand the error of your statement. No, this simulation does’t prove evolution. This simulation being correct doesn’t mean you evolved and that your ancestors were apes. You don’t have to be afraid of “giving even a single inch”.
So please stop making a fool out of yourself by making inane objections. Try to spend just a moment thinking about he matter without a desire to reach a specific conclusion biasing your thoughts. You can do it if you allow yourself.
Phoodoo, when a microbe replicates, which half dies? After a thousand generations, which is dead and which is alive?
Now the fun question. Suppose a bacterium having an inexhaustible food supply can replicate every hour. How many will there be in a week?
Rumraket,
You suggested that it was reasonable to have many layers of generations all reproducing at the same time, if we assume that the organism has no death cycle. Fine. Then your population is going to keep doubling and doubling the further you go, so the rate of fixation is going to be completely thrown out the window. If you start with a population of 5 after one round of births what is your population?
Death is a necessary part of the equation, but you want to skip that part so that it makes sense for 10 different generations all reproducing in the same time space.
“If the math is good, the logic is wrong, If the math is bad, the logic is right.” Just ask Joe.
Phoodoo, please explain what leads you to believe there are no deaths in the population.
That you don’t die of old age doesn’t mean you don’t die at all. There are still deaths in the simulation phoodoo.
This is why we laugh when you post.
Try 3: As discussed last time round if you feel capable of giving a set of rules I’ll code them into a similar simulation.
Uggh. Phoodoo, wake up. You’re babbling in your sleep.
Even with humans’ long, long time to reproductive maturity, we can easily have 3 generations reproducing at once. (Mother at 14, grandmother at 28, great-grandmother at 42). It’s common enough in the state where you live, Phoodoo, that it would never make the news. (Well, it might make the tabloids if Great-Grandmother were in the hospital giving birth on the exact same day as her granddaughter was 😛 but not if it’s just within the same year.)
For an organism with shorter time to reproductive maturity, of course we get more generations reproducing “in the same time space”. Ordinary house cats, not given any veterinary care, live an average of 7-8 years. That’s plenty long enough for Great-12th-Great-Grandmother to have a litter in the same season as her great-12th-granddaughter.
SO the MandM model is a realistic match to animals you are familiar with. Stop acting like an idiot and think about reality for a change.
Phoodoo: Suppose a bacterium can replicate every hour. That’s 1, 2, 4, 8…
How many will there be in a week?
And why?
In my summary of lots of population-genetic work on Moran Models, Wright-Fisher Models and diffusion process approximations, I should have added a bit more about work on the effects of overlapping generations.
If one wants a model that has more realistic age-dependent birth and death rates, to model particular cases with overlapping generations, take a look at my 1971 paper which is available for free here. It allows calculation of more realistic effective population sizes for such situations. Bill Hill (W.G. Hill) in the following year published his own treatment in Theoretical Population Biology which gave the expression in terms of the resulting variance in offspring numbers, neatly showing that classic formulas by Sewall Wright would then calculate the effective population size correctly.
phoodoo,
Just catchin’ up – bin away (Chile, thanks for askin’).
It would be a relatively simple matter to add a reproductive age and ‘realistic’ mortality to the simulation, such that choice of the MandM for reproduction and death is not quite so random (equiprobable wrt the entire population). However, I don’t think it will make a blind bit of difference to what happens – fixation of one colour. What do you think would happen, phoodoo – what fast one do you think is being pulled by leaving that complication out of the model? Are longevity and instant and perpetual reproductive capability the things that cause fixation?