ID proponents and creationists should not use the 2nd Law of Thermodynamics to support ID. Appropriate for Independence Day in the USA is my declaration of independence and disavowal of 2nd Law arguments in support of ID and creation theory. Any student of statistical mechanics and thermodynamics will likely find Granville Sewell’s argument and similar arguments not consistent with textbook understanding of these subjects, and wrong on many levels. With regrets for my dissent to my colleagues (like my colleague Granville Sewell) and friends in the ID and creationist communities, I offer this essay. I do so because to avoid saying anything would be a disservice to the ID and creationist community of which I am a part.
I’ve said it before, and I’ll say it again, I don’t think Granville Sewell 2nd law arguments are correct. An author of the founding book of ID, Mystery of Life’s Origin, agrees with me:
“Strictly speaking, the earth is an open system, and thus the Second Law of Thermodynamics cannot be used to preclude a naturalistic origin of life.”
Walter Bradley
Thermodynamics and the Origin of Life
To begin, it must be noted there are several versions of the 2nd Law. The versions are a consequence of the evolution and usage of theories of thermodynamics from classical thermodyanmics to modern statistical mechanics. Here are textbook definitions of the 2nd Law of Thermodynamics, starting with the more straight forward version, the “Clausius Postulate”
No cyclic process is possible whose sole outcome is transfer of heat from a cooler body to a hotter body
and the more modern but equivalent “Kelvin-Plank Postulate”:
No cyclic process is possible whose sole outcome is extraction of heat from a single source maintained at constant temperature and its complete conversion into mechanical work
How then can such statements be distorted into defending Intelligent Design? I argue ID does not follow from these postulates and ID proponents and creationists do not serve their cause well by making appeals to the 2nd law.
I will give illustrations first from classical thermodynamics and then from the more modern versions of statistical thermodynamics.
The notion of “entropy” was inspired by the 2nd law. In classical thermodynamics, the notion of order wasn’t even mentioned as part of the definition of entropy. I also note, some physicists dislike the usage of the term “order” to describe entropy:
Let us dispense with at least one popular myth: “Entropy is disorder” is a common enough assertion, but commonality does not make it right. Entropy is not “disorder”, although the two can be related to one another. For a good lesson on the traps and pitfalls of trying to assert what entropy is, see Insight into entropy by Daniel F. Styer, American Journal of Physics 68(12): 1090-1096 (December 2000). Styer uses liquid crystals to illustrate examples of increased entropy accompanying increased “order”, quite impossible in the entropy is disorder worldview. And also keep in mind that “order” is a subjective term, and as such it is subject to the whims of interpretation. This too mitigates against the idea that entropy and “disorder” are always the same, a fact well illustrated by Canadian physicist Doug Craigen, in his online essay “Entropy, God and Evolution”.
From classical thermodynamics, consider the heating and cooling of a brick. If you heat the brick it gains entropy, and if you let it cool it loses entropy. Thus entropy can spontaneously be reduced in local objects even if entropy in the universe is increasing.
Consider the hot brick with a heat capacity of C. The change in entropy delta-S is defined in terms of the initial hot temperature TH and the final cold temperature TM:
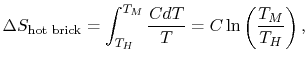
Supposing the hot temperature TH is higher than the final cold temperature TM, then Delta-s will be NEGATIVE, thus a spontaneous reduction of entropy in the hot brick results!
The following weblink shows the rather simple calculation of how a cold brick when put in contact with a hot brick, reduces spontaneously the entropy of the hot brick even though the joint entropy of the two bricks increases. See: Massachussetts Institute of Technology: Calculation of Entropy Change in Some Basic Processes
So it is true that even if universal entropy is increasing on average, local reductions of entropy spontaneously happen all the time.
Now one may argue that I have used only notions of thermal entropy, not the larger notion of entropy as defined by later advances in statistical mechanics and information theory. But even granting that, I’ve provided a counter example to claims that entropy cannot spontaneously be reduced. Any 1st semester student of thermodynamics will make the calculation I just made, and thus it ought to be obvious to him, than nature is rich with example of entropy spontaneously being reduced!
But to humor those who want a more statistical flavor to entropy rather than classical notions of entropy, I will provide examples. But first a little history. The discipline of classical thermodynamics was driven in part by the desire to understand the conversion of heat into mechanical work. Steam engines were quite the topic of interest….
Later, there was a desire to describe thermodynamics in terms of classical (Newtonian-Lagrangian-Hamiltonian) Mechanics whereby heat and entropy are merely statistical properties of large numbers of moving particles. Thus the goal was to demonstrate that thermodynamics was merely an extension of Newtonian mechanics on large sets of particles. This sort of worked when Josiah Gibbs published his landmark treatise Elementary Principles of Statistical Mechancis in 1902, but then it had to be amended in light of quantum mechanics.
The development of statistical mechanics led to the extension of entropy to include statistical properties of particles. This has possibly led to confusion over what entropy really means. Boltzmann tied the classical notions of entropy (in terms of heat and temperature) to the statistical properties of particles. This was formally stated by Plank for the first time, but the name of the equation is “Boltzmann’s entropy formula”:

where “S” is the entropy and “W” (omega) is the number of microstates (a microstate is roughly the position and momentum of a particle in classical mechanics, its meaning is more nuanced in quantum mechanics). So one can see that the notion of “entropy” has evolved in physics literature over time….
To give a flavor for why this extension of entropy is important, I’ll give an illustration of colored marbles that illustrates increase in the statistical notion of entropy even when no heat is involved (as in classical thermodynamics). Consider a box with a partition in the middle. On the left side are all blue marbles, on the right side are all red marbles. Now, in a sense one can clearly see the arrangement is highly ordered since marbles of the same color are segregated. Now suppose we remove the partition and shake the box up such that the red and blue marbles mix. The process has caused the “entropy” of the system to increase, and only with some difficulty can the original ordering be restored. Notice, we can do this little exercise with no reference to temperature and heat such as done in classical thermodynamics. It was for situations like this that the notion of entropy had to be extended to go beyond notions of heat and temperature. And in such cases, the term “thermodynamics” seems a little forced even though entropy is involved. No such problem exists if we simply generalize this to the larger notion of statistical mechanics which encompasses parts of classical thermodynamics.
The marble illustration is analogous to the mixing of different kinds of distinguishable gases (like Carbon-Dioxide and Nitrogen). The notion is similar to the marble illustration, it doesn’t involve heat, but it involves increase in entropy. Though it is not necessary to go into the exact meaning of the equation, for the sake of completeness I post it here. Notice there is no heat term “Q” for this sort of entropy increase:

where R is the gas constant, n the total number of moles and xi the mole fraction of component, and Delta-Smix is the change in entropy due to mixing.
But here is an important question, can mixed gases, unlike mixed marbles spontaneously separate into localized compartments? That is, if mixed red and blue marbles won’t spontaneously order themselves back into compartments of all blue and red (and thus reduce entropy), why should we expect gases to do the same? This would seem impossible for marbles (short of a computer or intelligent agent doing the sorting), but it is a piece of cake for nature even though there are zillions of gas particles mixed together. The solution is simple. In the case of Carbon Dioxide, if the mixed gases are brought to a temperature that is below -57 Celcius (the boiling point of Carbon Dioxide) but above -195.8 Celcius (the boiling point of Nitrogen), the Carbon Dioxide will liquefy but the Nitrogen will not, and thus the two species will spontaneously separate and order spontaneously re-emerges and entropy of the local system spontaneously reduces!
Conclusion: ID proponents and creationists should not use the 2nd Law to defend their claims. If ID-friendly dabblers in basic thermodynamics will raise such objections as I’ve raised, how much more will professionals in physics, chemistry, and information theory? If ID proponents and creationists want to argue that the 2nd Law supports their claims but have no background in these topics, I would strongly recommend further study of statistical mechanics and thermodynamics before they take sides on the issue. I think more scientific education will cast doubt on evolutionism, but I don’t think more education will make one think that 2nd Law arguments are good arguments in favor of ID and the creation hypothesis.

If Mr. Cordova is actually sincere in what he’s purporting to do here, he is likely to discover that the world of real science is rather less tolerant of deceit, lies, and misrepresentation of others’ views than is the world of ID.
Sal,
I think UD shoots itself in the foot on an almost daily basis.
While you have earned the opprobrium of many on the ‘anti-ID’ side for things you’ve posted in the past, I don’t have that extensive history. I only actively joined the ID debate last year (till I was silently booted off UD for no obvious reason). So to me, you appear genuinely interested in how the world really is, trying to reconcile that with your faith, rather than bending the world to fit. And you are keen that others in the ID community should also take a more rigorous stance with regard to the science they wish to critique. All of which I applaud.
Thank you for the kind words Allan Miller.
Petrushka and Dr. Liddle, and other members of Skeptical Zone. To answer some questions that might be in the back of some minds here.
1. I am merely an author at UD. I have no power whatsoever to unban individuals at UD whom the UD management has banned. Elizabeth has been gracious enough to allow me the privilege of authoring threads here at Skeptical Zone. I regret I do not have the power to reciprocate at UD, but if I’m able to get my website (CreationEvolutionUniversity) going, I will be delighted for the opportunity to reciprocate the kindess and hospitality she has extended to me here especially in light of the fact that she did so even though she was banned from UD.
2. I was once exiled from UD before by DaveScot. I’ve always been on thin ice there, but not with the ID community on the whole. Whether for good or not, I speak my mind. I don’t think I’ll ever change, and I’ll have to face the consequences of expressing myself freely.
3. The ID community does not have “creed” filters for participation, but the YEC communtiy does, and you can see that I don’t get along well with some of my YEC brethren.
In some YEC circles if you’re catholic or methodist or jewish whatever, you’re automatically out. You have the 7th day adventists YECs not exactly on great terms with the evangelical YECs.
I’m excluded from publishing in the YEC CRSQ peer-reviewed journal because I would refuse to sign their creed. I would have been excluded from becoming a student at ICR because I would have refused to sign their credal statements as a prerequisite for admission (not that I would want a degree from there anyway). I would be excluded from posting or hosting sessions at the ICC (International Creation Conferences).
Thankfully the Creation Biology Society (Kurt Wise, Todd Wood, Marcus Ross) would probably let me publish there. They were known as the Baraminology Study Group, and in 2004 they let even evolutionary biologist Richard Sternberg work as an editor! That of course led to a lot of problems for Dr. Sternberg.
Now why is there openess at the Creation Biology Society (Baraminology Study Group)? I suspect a lot has to do with the fact that Kurt, Todd, Marcus, and practically all the members matriculated through secular institutions like myself. This is true, for the time being with the ID leadership — they matriculated or are part of secular institutions. Curiously, Todd Wood is chilly regarding Intelligent Design. Sadly, I’ve not seen hardly any ID contingent at the Creation Biology Society (CBS). At the last meeting only Marcus Ross and I were the only ones with formal affiliation with ID….
4. The lengthy and fruitful discussion here at SZ would not be possible at UD because threads vanish from the front page in a matter of days, whereas, as you can see, this thread has stayed alive for 6 weeks. A forum (like ARNs format) would be a better format for lengthy and technical disucssions, and I’m working on it at my website….
5. I consider myself a proponent of ID, but an occasional critic of ID as well (as this whole thread should suggest). I consider myself not really a proponent of YEC, but a sympathizer, but also a somewhat harsh critic of YEC. I was a Theistic Evolutionist growing up, and nearly an agnostic.
6. I hope to post more criticism of ID (not many) and YEC (lots) at Skeptical Zone. Why? I’m trying to vet essays worthy of college level consumption. For example, Will Provine and Allen MacNeill assigned their students writings of Phill Johnson, Michael Behe, and Bill Dembski. Will and Allen might find such writings by ID authors flawed, they might find the writings disagreeable, but they found the scholarship of sufficient quality to be educational.
Even though at this stage, the discussion are in rough draft form, my dialogue here is an example of how I’m vetting some of the more technical topics. The topics may be obscure and boring to most, but that is the nature of technical literature.
I’m preparing a response to where I have disagreements with Mike. He is an expert in physics, but that doesn’t stop me from being skeptical of some of what he says, and I will state my reasons for skepticism of his claims shortly. We agree that Granville was wrong about the 2nd law, but it doesn’t mean we will agree on everything about entropy.
That said, I’m very grateful for Mike and Oleg’s corrections of my errors, and I expect they will correct many more. I don’t look at this as bad. The short term humiliation of being shown to be wrong is the worth the price if one will come away with lasting truth.
This may not quite describe their reason for such assignments. There is a difference between being articulate and being scholarly. Each of these authors has been corrected, extensively and in detail, on every statement they’ve made. Their response is (1) to ignore all corrections and either repeat error or just drop the subject; and (2) to carefully avoid anything resembling peer review. These are not the actions of scholars.
If you wish to truly understand the vacuousness of ID, you’re not going to assign a class to read the excretions of Dave Scott, Barry Arrington, Gil Dodgen et. al. You instead go to the “thought” leaders to see how well they support their arguments and how they respond to the sort of criticism peer review would have provided.
If Creationism / ID were amenable to correction, it would have died already. Remember Creationists must work back from their ‘conclusion’ – anything which completely defeats this must be ignored.
Rich has it dead right.
I have no idea where Sal gets his notion that the “scholarship” of the ID leaders is of sufficient “quality” to be educational. Those of us who dig into their writings (I have been at this for well over 40 years now) do so to catalog their misconceptions and misrepresentations of science. The only real “value” in that is to improve pedagogical methods, debunk their propaganda, and to educate the public.
Debating them only gives them the fake legitimacy they crave. Celebrity and high visibility have always been important to ID/creationists; as they are to most crackpots who pester scientists for a free ride by feigning ‘knowledgeable critiques’ of the evidence and theories in science. These kinds of crackpots have been hanging around various science departments at universities for many decades if not for centuries; and they all believe they are original.
ID/creationist “scholarship” has always been atrocious to its core. It’s bloated, pretentious, and dead wrong. The history of this goes back to probably A.E. Wilder-Smith, from whom Morris, Dembski, et. al. have acknowledged taking inspiration.
After being debunked repeatedly, ID advocates want to distance themselves from the bumptious Duane Gish and the rabble rousers at ICR and AiG (and one can easily find over at the ICR and AiG that the hostile feelings are mutual). They then concoct pseudo-philosophy and pseudo-history in order to make themselves appear to have a history of original thought. Yet the same crackpot misconceptions and misrepresentations about science that they inherited from Morris and Gish, as well as from Wilder-Smith, permeate all their writings. The YECs are just more crassly open about it; sectarian dogma first, all else bent and broken to fit. The ID people want to appear intellectual and “objective;” but they just end up appearing pretentious.
Mike,
Thank you again for the generous time you’ve devoted to this discussion. It has been educational for me. However I have some disagreement regarding the spatial component of entropy and it has some relevance to the Origina Post where I described colored marbles.
I would post things here in this blog, but it’s a royal pain to write math in this venue. Thank you for bearing with this difficutly by reading my MS Word responses. The document is here:
http://www.creationevolutionuniversity.org/public_blogs/skepticalzone/2nd_law_sewell/configurational_mixing_thermal_entropy.doc
A link to the chapter in Gaskell’s book is here:
Configurational Entropy
Thank you again.
“Configurational entropy” is a concept that leads to some of the most insidious confusion in the learning processes with students. Introductory courses at the undergraduate level don’t usually use it. In advanced courses, the presumption is that these students understand that differential energy exchanges are involved in particle interchanges; but that is not safe to presume. Instructors do well to review basics if they want to use it.
Entropy is about ENERGY microstates. If it’s not about energy, it’s not about entropy.
When talking about matter in a vapor/gaseous state, the volume of phase space, containing the energy states consistent with the macroscopic state of the system, is usually the most efficient way to enumerate energy states. Changes in volume appear as changes in entropy because the walls of the container do work on the gas. And the reason that happens is because matter interacts with matter; i.e. the walls and gas interact.
Working with ideal gases to learn concepts of entropy take students into a number of nasty apparent paradoxes that have to be dealt with in basic thermodynamics and statistical mechanics courses. The best statistical mechanics textbooks skip over ideal gases and go directly into the enumeration of energy microstates. Whether they use the Einstein oscillator system, the two-state system or some other system, the best approach is to start out with the concept of enumerating ENERGY microstates.
After one has learned what entropy is, one can go back and deal with the paradoxes of an ideal gas from the microscopic perspective.
Only if an interchange of particle positions describes a different energy state can we say entropy folds in particle positions. If the molecules or atoms are identical, interchanging them does not change the energy state. Such an interchange does not change how momentum and kinetic energy are exchanged among particles. At the atomic/molecular level, there is no such thing as an infinitesimal difference between atoms/molecules, nor is there such a thing as an infinitesimal difference in their interactions with their surroundings. They are either different or they are the same.
If unbound particles are different, interchanging them may very well cause a change in the number of energy states; and this can only happen because the particles interact not only with each other, they interact with other particles in their vicinity. This is usually expressed in the form of the “chemical potential,” which is the energy per particle required to add or remove a particle from a collection of other particles. Taking out a particle that does not interact strongly with its neighbors, replacing it with another that interacts more strongly, and then putting the first particle in the place where the second particle was, produces another countable energy state, hence a change in entropy.
Gases are only a very small subset of systems to which the concept of entropy applies. You can talk about the interactions at boundaries of systems as atoms and molecules diffuse; and that gets you into energy and momentum exchanges that affect the number of ENERGY states.
But it is always, ALWAYS, about the number of ENERGY MICROSTATES. The position of things is only incidental. Entropy changes only if energy is exchanged among microstates in the process of changing the positions of particles. That can only happen if matter interacts with matter differentially in the exchange.
This is where some textbook authors have been sloppy. “Configurational entropy” gives the impression that the mere spatial arrangement of things causes changes in entropy. If the particles do not interact in any way, or if there is not a differential in the interactions, there is no change in entropy because no changes in the energy/momentum exchanges take place; which means there is no way existing energy states can be redistributed into more or fewer numbers.
If one adds/removes a little energy to/from a solid, such that the solid merely changes its internal energy without starting to come apart, the mean positions of all the atoms of the solid remain the same. Yet the entropy changes.
Did you work though the comparisons between the two-state system and the Einstein oscillator system and make the plots of temperature versus energy? What were your results?
Incidentally; I would not use Gaskill’s book. There are far better books about materials that are more careful about such things. And they don’t encourage double counting with notions of “configurational entropy” in the way Gaskill does it.
Placing two crystals next to each other might result in the diffusion of atoms of each into the other; and this is highly temperature dependent. It is that temperature dependence that provides a critical clue that energy exchanges are taking place among atoms at the interface between the two crystals.
As you should know from even high school physics, those atoms are not going to budge unless there is a potential gradient (force) that breaks them loose from their sites and causes them to move across the interface. That gradient arises because of a number of reasons that depend on the particular atoms, their binding energies, and temperature. Lower the temperature and the migrations across the boundary decrease.
The chemical potential I mentioned above might, for example be different for different crystals. Place them in contact on an atomically smooth interface and that difference will cause atoms to break bonds and migrate across the boundary.
Notice that even Gaskill says, in a very imprecise way, that this process continues until “all concentration gradients in the system have been eliminated.”
This is a very poor choice of words. Concentration refers to the number of particles per unit volume. It isn’t “concentration gradients” that cause particles to move; it’s potential energy gradients. Particles are going through energy changes; and as a result, the energy microstates in the system are changing. Therefore entropy can change.
There would be no distinction between thermal entropy and “configurational entropy” IF one counted the energy exchanges properly with each exchange. Those energy exchanges depend on temperature and on how many atoms have already diffused across the boundary. But the notion of “configurational entropy” results in double counting; and it doesn’t even get the calculation correct because one is forgetting about the changing chemical potentials near the boundary in the double counting.
This is the wrong way to count microstates if one doesn’t take into account the energy exchanges and then also piles this count on top of whatever other counting one does.
And it will not check out in the lab.
(I was going to put this part of the response off until you had a chance to mull over the above response; but my schedule is busy and I don’t know when I will be able to reply again.)
Mike,
Thank you again for your time.
Agreed. And I will re-write my essay accordingly. There are more accurate ways to describe gases such as the Van der Waals equation of state and Virial expansions. Thank you for the criticism, I will make amends in my essay. The ideal gas was an un-necessary confusion factor on my part.
To clarify, my terminology is:
Volume, unless otherwise stated, is physical volume not volume in phase space. Unfortunately “V” is often used in derivations (even in books like Pathria), and it is up to the reader to discern if the “V” is for physical volume or “V” of phase space volume.
Analysis of microcanonical ensembles involves analysis of phase space whose phase space “volume” is defined usually by multidimensional integrals of momentum and position or quantum states, but this is not physical volume, but phase volume.
However, the “V” in Ω(N,V,E) in Pathria is physical volume not phase volume, and likewise the “V” in the mixing entropy calculation is physical volume, not phase space volume.
I will do that. I was working on the Magnetic Dipole example, and I will add the Einstein Oscillator to my list of things to do. It will take me a little time to do that and revise my essays in light of some of the things you said such as:
Out of respect for your time, I’ll refrain from posting on this thread until I’ve reviewed the Einstein Oscillator. Thank you again.
Quick slightly OT comment to Sal.
See how pi looks here:
I did that with:
dollar-sign latex \pi dollar-sign
This seems to be supported by wordpress. (Or maybe not – I’ll see when I press the post button).
Quickly, before my day starts.
Spatial volume, volume of phase space, spatial order, and entropy are all completely different concepts. There should never be any excuse for conflating any of them with each other; even if entropy, for example, sometimes involves spatial volume and/or phase space volume.
Volume localizes. It doesn’t determine order. What is contained within a volume may or may not be ordered.
Order has to be defined carefully, and it usually involves a specified convention. Disorder deviates from that convention. Measures of disorder usually involve counting the number of permutations required to bring the disorder back into the conventional ordered state.
Furthermore, there is no such thing as the entropy of collections of letters of O and H. Letters O and H have no interactions and no concomitant energy states even though they may have some conventional alphabetical order.
But the elements O and H do have interactions and energy states.
Furthermore, one can only use things like ∑p(i)ln(p(i)) when one can legitimately talk about the probabilities of various energy microstates. And this calculation can only maximize spontaneously if the constituents of a system can interact in such a way that they can exchange energy among themselves after the system has been isolated from a larger environment.
I’m away for the rest of the day.
Mike Elzinga wrote:
I don’t think so. Energy is not all that special and entropy can be defined with or without regard for it. Entropy is merely the logarithm of the phase-space “volume” available to a physical system.
A system in some initial state travels through phase space as time goes on. Unless we know the initial state with absolute certainty, pretty quickly we lose the ability to predict where exactly the system is. For all we know, it is somewhere in phase space, with a uniform probability distribution. In this case, entropy is the logarithm of the volume of the entire phase space.
Often the dynamics of a system is constrained by conservation laws. Although coordinates and momenta change, certain quantities never do. Energy is one example, but not the only one. The number of particles, total momentum or angular momentum can also be conserved. Conservation laws limit the ability of a physical system to explore all of its phase space and restrict its “diffusion” to “layers” in phase space with a constant energy (and/or particle number etc.). In this case, the system can be found with equal probability as long as it has the right energy (and/or particle number etc.). It populates a layer of constant energy (and/or particle number, etc.) with uniform density. Entropy is then the “volume” of that portion of the restricted phase space that is available to the system.
So energy is not all that special. It enters thermodynamics on a par with other conserved quantities.
The ergodic theorem and sensitivity to initial conditions are fascinating topics that require a firm foundation in the basics and a more mature grasp of the mathematics as well as a good understanding about how matter actually behaves as opposed to how it is often portrayed ideally in mathematical form. One cannot address these topics without that advanced understanding of matter-matter interactions with photons, phonons, and other particles going off to infinity.
However, when we are working with beginning students, or with students who have absorbed the serious misconceptions and misrepresentations of the ID/creationist movement, or with the general public, we need to get back to the basics that precede even introductory thermodynamics.
The early concepts need be discussed carefully during the time the students are maturing in their math as well as learning the concepts themselves. That is why several long-respected authors of undergraduate textbooks (e.g. Kittel, Reif, Zemanski, etc.) picked systems that are simple and easy to work with mathematically.
Reif, for example, mentions those ideas about phase space very early in his book but doesn’t get into the issues of the ergotic theorem until very late in the book. While I like Reif, I would have organized his book differently in the light of more recent pedagogical findings; but I certainly would not put the ergodic theorem up front.
Going all the way back to Clausius, entropy has a close connection with energy; he defined it that way on purpose (he even said so) although he didn’t know what we know today about microstates, nor did he even know for sure what temperature really was other than that it was an empirical measure of “degrees of heat.”
There are very good pedagogical reasons for making sure students know they are talking about energy microstates instead of spatial order. Not only have sloppy popularizations contributed to the confusion, but creationists like Henry Morris and Duane Gish have hammered on this misrepresentation for decades in order to confuse biology teachers and the general public. The effect of this misinformation has been far out of proportion to the numbers of ID/creationists because they leveraged the popular media so effectively.
Those other forms of “entropy,” such as Shannon entropy may use some of the same formulas, e.g., – ∑p(i)ln(p(i)). It is the average of the logarithm of the probabilities, but those probabilities could be about anything. It is just a mathematical summation whose behavior is independent of how it is interpreted; and it maximizes when all probabilities become equal, in which case it becomes the logarithm of the number of things being counted. It is the context and concepts of its use that are different even where bits correspond to the energies required to flip them. This is no different from any other mathematical expression that finds use in a number of fields.
There is another reason to keep students focused on the energy connection; matter interacts with matter. This is the most frequently overlooked part of the misconceptions about the behavior of isolated systems as they come to equilibrium; it leaves the impression that instructors are just hand-waving about how systems come to equilibrium. Yet there is important physics going on here. If it were not for those interactions, we would not be able to claim that such isolated systems come to equilibrium and the entropy spontaneously maximizes. That spontaneity involves exchanges of energy.
One can’t always say that about other sets of probabilities concerning events or objects that do not interact among themselves to redistribute those probabilities. It’s not true of mixed up alphabets or of decks of cards. Those things don’t interact spontaneously among themselves to increase the probability of their state; and those states are matters of human convention anyway. There are no charge-to-mass ratios equivalent to what we see for atoms and molecules and condensed matter.
There are literally thousands of subtleties in condensed matter and in chemistry that one encounters in the lab as well as in well-studied applications. Students and the interested layperson will very likely not have had these experiences. Much of what we know and work with in chemistry and condensed matter is not yet sufficiently well quantified; and even where it is, it is complicated and messy, requiring supercomputers to demonstrate. That is as true of the formation of galaxies in the presence of star formation and supernovae explosions as it is of the formation of all other types of condensed matter. And it all involves multiple forms of energy exchanges.
If you haven’t already read it, you might be interested in a recent “popularization” by cosmologist Sean Carroll, From Eternity to Here. He delves into all the subtleties of entropy; but he also makes me cringe in his careless equating of entropy with disorder early on in the book. Nevertheless, he gets into issues like the ergodic theorem as it might apply to the entire history of the universe; and he brings up many of the problems that are under current investigation. Yet he doesn’t appear in this popularization to recognize the importance of the processes involved in condensing matter. Many of the possible solutions to those issues he raises are found in those processes of radiation of energy as matter clumps and binds together.
I think many of us who have dealt with students from the high school level to the graduate level are aware of the uncomfortable fact that no matter what level these students are at, many of them are carrying serious misconceptions that go all the way back to basic high school physics. Thermodynamics and statistical mechanics and the concept of entropy have been the focus of much pedagogical research and discussion. But the problems caused by bad popularizations and the ID/creationists still persist, and instructors need to be alert.
Mike Elzinga wrote:
No, Mike, these are really basic things that go to the heart of statistical physics. And they do not require complications such as scattering, photons etc. They do require some sophistication, but you will be amazed how little. It’s true that you can’t get ergodicity in any form if you work with a harmonic oscillator, that old favorite of textbooks. But add just a dash of anharmonicity, and you get the microcanonical ensemble on a silver platter. In fact, the familiar pendulum is a no-frills system that provides a basic illustration of the microcanonical ensemble.
Eh; you misconstrue my point.
Yeah; producing a stationary Lissajous pattern on an oscilloscope and then detuning one of the oscillators slightly has been around “forever.” And the anharmonic oscillator is also fairly standard. Neither were very stimulating demonstrations. More analytics, fewer simulations back then.
I love the Applets. Now that students are generally required to have powerful laptop computers with nice software packages available for programming up simulations, or are simply able to go to the websites of a number of physics simulations, it is certainly feasible to work it into a course earlier. I retired just as much of that laptop computer technology was becoming convenient and relatively inexpensive to use and well before Applets. It was still pretty much a choice of what one had time and money for, and it was often hard to get the money to fund it. And we certainly couldn’t demand that students bring their own computers.
In my own research lab, I had to write everything from scratch, including all the graphics and the lab instrument interfacing protocols (for those instruments that provided IEEE interfaces; not many at the time).
What level of students do you teach; undergraduates, graduates? Where in the course do you introduce these ideas, and with what kind of exercises? How do you use this to lead into and motivate later topics?
What are you finding out about whatever misconceptions your students battle with in your course? It would be nice if we are now far enough away from that blitz of misconceptions promulgated throughout the 1970s into the late 1990s that the efforts to deal with the “entropy problem” have finally taken effect. It would make this old geezer feel good. 🙂 Since retirement I’m off onto other things now.
@Oleg
I was just reminded after looking at your link that I had a former submarine shipmate, Charlie Darrell who worked at APL. He retired in Jan 2011. Any chance that you had met him him?
Mike,
These days I teach courses taken by mostly graduate students, with a few very brave (and smart) undergraduates. This particular applet will be used at the beginning of statistical physics to illustrate the basic notions.
The APL is on a different campus, 20 miles away from ours. There isn’t much overlap between them and us, just an occasional collaboration here and there.
Mike wrote:
I will be glad to point out that this is the opinion of one physicist, however, it is evident that another physicist feels comfortable teaching his students otherwise. So, I feel quite comfortable saying entropy is not only about energy microstates.
As I promised, I went ahead and plotted the temperature vs. energy of the two-state system and the Einstein oscillator. I also provided a small comment as to why configurational entropy will not result in double counting thermal microstates and distorting thermal results.
http://www.creationevolutionuniversity.org/public_blogs/skepticalzone/2nd_law_sewell/plots_configurational_entropy.doc
but I have really nothing of substance to add to what Oleg said regarding Entropy not being only a function of energy microstates.
When I posted this thread on July 4, I had only been studying thermodynamics and statistical mechanics for a few weeks. Some of my understanding has been changed since I first wrote the post, but I see nothing substantially wrong with my original points.
Thanks to everyone on this thread for the comments, I don’t have much to add to what has already been said in this thread. I may post on thermodyanics and entropy again in the future, and this discussion was very helpful to my understanding.
What are you suggesting here; that you can believe anything you want as long as you make sure you maintain fuzzy notions about science so that you can point to “disagreements?” That shtick is one of the oldest and moldiest of creationist “debating” tactics. Get over it.
Some instructors use it in the cases of explicit examples; but they use it with the understanding that there are energy differentials taking place in the exchanges – unless they are explicitly counting something else; and then they would say what they are counting. One doesn’t have to use “configurational entropy.” You can use classical thermodynamics with experimental data in many cases. Discrete counting has to agree. You can also look at any solid state device book and see how junctions between P-type and N-type semiconductors are treated. No configurational entropy despite the fact that electrons and holes migrate across the boundary. Similar analyses can be done for diffusing gases, liquids, or solids.
Counting energy differences as a result of particle interchanges can be done and a “configurational entropy” change can be calculated. But no physics instructor I have ever heard of misses the energy part of these exchanges unless they are talking explicitly about a different kind of “entropy” that has nothing to do with energy microstates. Just because you insinuate that they do doesn’t make it so.
If you don’t get the point of ∫dQ/dT, then you don’t understand entropy. Why would you think it doesn’t involve energy? Why do you insinuate that matter doesn’t interact with matter?
We all know about those other “entropies.” So what? Just because the formulas are the same doesn’t mean they are about the same thing.
Anyone can take averages of the lengths of lizard tails, or the averages of car fleet mileages, or the averages of the logarithms of the probabilities of energy microstates, or the averages of the logarithms of the probabilities of just about anything, including lizard tails; but that certainly doesn’t make all of these things the same.
This statement is pure gibberish. If you still think particles moving across junctions and interfaces without a change in energy cause a change in entropy without specifying what “entropy” you are talking about, that is your problem. You are simply demonstrating that you don’t even understand Newton’s laws.
You are also missing one of the most fundamental facts of nature; namely that matter interacts with matter and matter condenses. Chemists and physicists have spent a few centuries now learning about those interactions by taking matter apart; and that requires the input of energy. Marbles, dice, cards, and alphabets don’t interact among themselves the way atoms and molecules do.
If you would even remember your basic high school physics, you would be able to figure out how the energies of interaction among atoms and molecules would scale up if marbles or bowling balls, for example, had equivalent charge-to-mass ratios and quantum mechanical rules. And “gases” of marbles and bowling balls would also have to have kinetic energies associated with constant motion of these “particles.” How would that come about?
I’ve spent years in the lab using this stuff. I have designed, built, and used equipment based on these ideas. Experimental techniques in thermometry are based on these ideas. Cooling techniques, such as adiabatic demagnetization, are based on these ideas. Photon-phonon cooling techniques are based on these ideas. My dilution refrigerators most certainly used the ideas of the energies involved in mixing and evaporation of fermion/boson mixtures of helium 3/helium 4. There is no way you can know what you are asserting.
Get hold of a decent thermodynamics and statistical mechanics text and take a course at a good physics department. But as it stands at the moment, it appears that any instructor will be wasting time trying to teach you thermodynamics and statistical mechanics when you still haven’t learned basic high school physics, let alone assimilated basic facts about the universe around you.
Mike,
I was merely trying to accomodate your insistence that:
That is not is what is taught at Oleg’s school. He gave excellent justification of his points.
A professor at Purdue whose text I provided also gave justification. I also provided and example where dq = 0 but you have an entropy increase based on Pathria and Beale (a good physics text). Even more advanced concepts of entropy such as suggested by the Bekenstein bound suggest entropy is more than energy micro states.
<blockquote>
If you still think particles moving across junctions and interfaces without a change in energy cause a change in entropy without specifying what “entropy” you are talking about,
</blockquote>
The issue is total energy change of the system, not the energy change of individual particles. The mixing entropy case with dq=0 and dE=0 for the system is an example. Something you have not be able to refute.
Any way what you have said otherwise is very educational, but your insistence that:
is dubioous. You said
So how does mixing entorpy increase with dq=0 and dE=0? Is mixing entropy one of the other “entropies” or is it entropy that indicates a change in the number of energy microstates?
I have a box with two gases in thermal equilibrium separated by a barrier. I remove the barrier Are you saying there are MORE energy microstates simply by removing the barrier? Do you feel comfortable teaching students that mixing different species of gases at thermal equilibrium and thermally isolated increases the number of energy microstates? Are you comfortable saying the mixing entropy increase is the result increase in the number energy microstates? I’m not. But if you insist, I’ll say:
Mike says “the increase in mixing entropy is an increase in energy microstates”
I’m not a scientist, I’m a finaceer. But if I interpret what you are saying, you don’t think I could apply to a descent engineering school, get accepted, study statistical mechanics and pass the course, let alone get a good grade. Ok, according to you I guess I should just fold.
But I have two questions,
1. does change in mixing entropy, imply a change in entropy?
2. does change in entropy always imply a change in the number of energy microstates?
Don’t get too cocky, Sal. Your grasp of thermodynamics and statistical physics is rather tenuous. Teaching Mike Elzinga basic stat mech is above your pay grade.
For example, a “change in mixing entropy” is a redundant expression. Mixing entropy is, by definition, a change in entropy (which results from mixing of two gases). So your question makes no sense.
Does the mixing of gases in the case I described imply an increase in the number of energy microstates with dq=0 and dE=0?
What is the correct answer? I can’t see how simply removing a barrier in the case adiabatic isothermal mixing will increase the number of energy microstates.
My understanding is tenuous, so I’d like to know if my assertion is correct or incorrect. I would presume this is a question that a student of physics would be curious about.
This question has a high gibberish content and needs to be triple-distilled before it can be answered. Here is my attempt at translating it.
What you presumably mean is this. Take a thermally insulated container containing two gases separated by a heat-conducting barrier. (dQ=0 means no heat is transferred to the container from the outside.) Count the number of microstates with a given energy E. Open the barrier to give the molecules of both gases access to the entire container. Count the number of microstates (at this same energy E of course). Has it increased?
The answer is yes, provided the two gases were composed of different molecules (e.g. oxygen in one half, nitrogen in the other).
There are two usages of how “ENERGY microstates” are counted in this thread:
1. the counting of microstates is done without consideration to physical position
2. the counting of microstates is done with consideration to physical position
I’ve argued for #2, that physical position can be considered in the counting of microstates, and that is consistent with Olegt’s answer:
That agrees with what I said regarding entropy change due to mixing:
Mike specifically used the phrase “ENERGY microstate”, earlier he asked:
“Why don’t you try to explain what the color of marbles has to do with the number and distributions of energy micostates? ”
The marbles were analogous to mixed species of gases where the thermal entropy doesn’t change (because the process is adiabatic):
When Mike uses the phrase “ENERGY Microstate” that appears different than the usage of microstate in Olegt’s reply. But Mike is in the best position to answer whether the microstate of a particle is only about its energy or whether the definition of microstate involves position? Mike said:
The change in entropy due to mixing is a counter example to this claim. Spatial configuration matters in the calculation of total entropy (but not necessarily thermal entropy).
Mike argues the microstate is not described by position at all whereas in the example I gave, the number of microstates increases because more physical volume is available to the molecules of each species, which implies that the number of microstates has some dependency on position, not just the energy of the particles.
Hence, I cannot in good conscience agree with Mike’s claim:
unless we are talking purely thermal entropy or some specialized cases.
Other than that, I’m happy to agree with Mike on many other points, but since the discussion of the entropy of mixing was in my OP, I felt obligated to defend it or retract it based on this discussion. The illustration of marbles and mixed gasses in the OP still stands.
HT:
Thanks to Neil for finding a solution to using latex. I ported equations from the file that I wrote into Latex here.
I think (but I ain’t no physicist) that the difference may be that two different gases at the same temperature must have different energies, because they have different molecular/atomic weights and hence this will affect kinetic energy. If you remove a barrier between two volumes of a single-species gas, there has been no change – there is nothing to equilibrate; they start off in complete equilibrium. But between two different gases, as they diffuse into each other they transfer the differential kinetic energy about the collection and one could (in principle) do work as that equilibration takes place.
It must have something to do with spatial configuration … but that spatial configuration is about energy distribution. My two cents – IANAP!
stcordova on August 31, 2012 at 4:07 pm said:
Sal, you are tilting at windmills.
Forget about gases, take a single particle, in the classical approximation. “Counting its microstates” means counting the volume of phase space available to it. The phase space of a single particle is six-dimensional: it includes three coordinates and three momenta. So counting microstates is done with consideration of the particle’s physical location. By definition. There is no point in pinning Mike on this. This is one of the basic points people learn at the beginning of a stat mech course.
One can argue whether one should include microstates corresponding to a fixed energy (microcanonical ensemble) or in contact with a thermal reservoir (canonical), but this would be beside the point.
That is my understanding, and that is why I had an issue with his statement:
Because I don’t know as much as you and Mike, I just wanted to make sure I understood the correct way to characterize things.
That is my understanding, and that is why I had an issue with his statement:
Because I don’t know as much as you and Mike, I just wanted to make sure I understood the correct way to characterize things.
So regarding Mike’s statements:
Mike: agrees
Olegt: disagrees
Sal : disagrees
Mike: agrees
Olegt disagrees
Sal : disagrees
“Sal, you are tilting at windmills.” I’m fine with you saying that, you and Mike know far more than me, and you teach at a very fine school. I defer to you on these matters.
Me:
Driving into town, it struck me that this is probably horse feathers – the energies will be equilibrated, because the compartments have equilibrated temperature. The differential mass must give a differential in mean particle velocities (?).
Notice the phrase I have highlighted.
You seem to think I was born yesterday. Let me tell you something.
I have been watching the ID/creationist shtick for well over 40 years. We picked up on the shtick you are using way back in the mid to late 1970s. It is easy to spot; one has only to watch a single debate between a creationist and a scientist to see it. It has been the standard operating procedure of ID/creationists ever since Morris and Gish started the ICR and taunted scientists into staged campus debates.
The creationist tosses out a load of bullshit. The scientist refutes it and tries to explain the real science. The creationist ups the ante by jacking up to advanced topics. He throws out phony “disputes” among scientists. He tosses out equations and concepts that he doesn’t understand and then babbles gibberish about it.
The scientist tries to explain, but the creationist and his audiences aren’t listening. They don’t care. They don’t know and don’t want to know.
The creationist is now feigning the appearance of being the expert in all things who can smash any scientist into the ground with just his pinky or his deft turn of phrase. He thinks he is giving the appearance of being a ringer who just lured a hapless scientist in close and then sucker punched him. He already won the debate just by getting on the same stage with the scientist and letting the celebrity of the scientist rub off on him.
This is what you are doing. You have a short but intense history of this sort of “debating” tactic on the internet. You attempt to set yourself up as a professional equal to those you lure into engaging you. Floyd Lee, who shows up regularly on Panda’s Thumb, uses exactly the same tactic. Unfortunately, you look like an idiot with your feigning interest and then countering as though you know something scientists don’t. And, as far as you are concerned, I am a nobody from nowhere; so you get nothing from “debating” me.
I learned long ago to never debate ID/creationists. I engaged you because I wanted to find out if you had learned anything from your failures in science. Obviously you have not. You simply illustrate that ID/creationist zealots use the same socio/political tactics creationists have always used. It’s getting pretty boring after over 40 years.
So I have no intention of trying to give you a complete course in thermodynamics and statistical mechanics. You do that for yourself.
stcordova on August 31, 2012 at 4:07 pm said:
Not sure I understand what this means. What’s “thermal entropy” and what’s “total entropy”? Can you give an example where the two notions are distinct?
From what I can gather from Sal’s exchanges with Sewell over at UD, ID/creationists are still looking to preserve that “fundamental law of physics” that prevents the origins of life and evolution. Everything has to fall apart into decay; otherwise there can be no such thing as Sanford’s “genetic entropy” and the rescue from decay by “information” and “intelligent design.” There must be the Fall by physical law and Redemption by divine interaction.
So apparently they still believe there is some form of entropy that fills the bill, and that it has something to do with arrangements of particles. Mixing entropy or configurational entropy must be it because mixed up things, like different colored marbles or buildings ripped up by tornados, are difficult to assemble back into completely ordered sets.
Sal’s and Sewell’s problem – as near as I can piece it together – is that they seem to think that any entropy calculation that involves spatial positions must therefore mean that entropy is intrinsically about spatial order or arrangements; or perhaps that there are “different” or “advanced” entropies in thermodynamics and statistical mechanics, one of which will come to the rescue of ID/creationist assertions about origins of life and evolution.
It is the same kind of mistake one would make if he were to assert that taking averages is always about lengths because there are people who take averages of lengths. The concept of taking averages has nothing to do with length.
You are correct that the mean velocities of two different gases at the same temperature and pressure are different. This is why phase space is such a useful concept; it places positions on one set of axes and momenta on the orthogonal set. The force on a unit area of the box is the average time rate of change of momentum of the gas molecules reflecting from the walls.
But what does this mean for, say, that two-state system of atoms embedded in a matrix of other atoms that are not participants in the energy exchanges? Spatial position has nothing to do with entropy in this case.
Let’s try some step-by-step comparisons.
(1.) Does the concept of adding have anything to do with money even though one can find many examples where money is being added?
(2.) Does the concept of averaging have anything to do with ages of members of a population even though one can find examples of where ages are averaged?
(3.) Can you average the logarithms of the ages of members of a population?
(4.) If you know the numbers of ages in specified age ranges within a population, can you calculate the probability of finding a particular age?
(5.) If you know those probabilities of ages in a given population, can you find the average of the logarithms of those probabilities?
(6.) Does averaging the logarithms of the probabilities of the ages in a given population calculate the entropy of a population? What would that mean?
(7.) Does averaging the logarithms of the probabilities of energy microstates in a thermodynamic system calculate the entropy of a system?
(8.) Can you give a reason why the concept of entropy has to be about spatial configurations?
(9.) How does saying that the concept of entropy has nothing to do with spatial configurations any different from saying that the concept of averaging has nothing to do with ages?
(10.) If you wouldn’t insist on asserting that the concept of averaging has something to do with ages, why would you insist that the concept of entropy has something to do with spatial arrangements?
(11.) What is different about entropy in your mind?
(12.) Do you believe entropy applies only to particles flying around in space?
(13.) Why are spatial coordinates considered in calculating the entropy of gases?
(14.) Define order. Define disorder. How are order and disorder measured?
(15.) How does the calculation of the average of the logarithms of the probabilities of energy microstates measure disorder?
(16.) How does ∫dQ/dT measure disorder? What is disordered?
The material science book by Gaskill makes this distinction. I provided a link to the chapters available online in his book. He teaches at Purdue. If the terminlogy is erroneous, I would welcome a correction, but that seems to be a common engineering convention in material science. Walter Bradley (also a materials scientists like Gaskil) uses exactly the same convention that Gaskill uses.
Here is my understanding, and please correct me if this is wrong. I have serious issue with Mike’s statement:
whereas you said (and which I fully agree):
My own thinking to explain Gaskill’s distinction and reconcile entropy being defined by spatial configuration follows below.
From the classical approximation (which is corrected by quantum mechanics), there is a phase space, as you said, defined by momentum and position.
In classical mechanics, the state of a particle is defined by position and momentum, whereas in quantum mechanics it is different. However Gibbs was able to make a good approximation using classical mechanics. And I’ll first start with the classical approximation before going into the quantum mechanical description since that helps give a conception. Even your pendulum example takes advantage of the classical definition of phase space.
For a single particle, the description of the microstate is given by position and momentum. But becuase in classical mechanics the position is continuously defined rather than quantized, Gibbs sliced up the position by defining the position in terms of slices or small bins. The slices had length of some arbitrary value (let us call it h, but not the h of Planck’s constant in this case) and the bins had volume of h^3. Thus it became possble to count a finite number microstates.
So if we have a particle in a volume, the number of small bins the particle can be found in is:
where the subscript Conf1 is indicating this pertains to the spatial configurational component of the microstate for particle 1. For N paritcles:
Gibbs had to make a similar trick for putting momentum in bins so that the number of microstates would be finite.
Because energy can be defined independently of position, the total number of microstates is the number of possible spatial configurations multiplied by the number of energy configurations, symbollically it can be expressed as:
Where the subscript Th relates to the energy aspect of the mirostate
Using Boltzman’s formula for the Total entropy S:
However noting:
![Rendered by QuickLaTeX.com \frac{\partial S_{Conf}}{\partial E} = \frac{\partial}{\partial E} \left[ k_{B} \ln \Omega_{Conf} \right] = \frac{\partial}{\partial E} \left [ k_{B} \ln \left[\frac {V} {h^3} \right]^N \right]= 0](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20384%2032'%3E%3C/svg%3E)
we are able to recover the notions of classical thermodynamics being about the distribution of energy among microstates without consideration to spatial configuration. For example:
But whether my derivation is wrong, fundamentally you are right and Mike is wrong regarding his erroneous claim:
I accept everything you say about me, that my understanding is tenuous, that what I may state is gibberish, that I don’t know anything about physics, etc. I respect and accept you judgement on these matters. However, I fully agree with you that what Mike said is wrong. You are right, and he is wrong.
Finally, I provided the classical approximation as distilled from Gibbs ideas, but since the energy aspect in the counting of the micrstates is separable from the spatial aspects of the counting of microstates, it stands to reason we can simply resort to counting the ways that energy is distributed in a system and drop the spatial aspects if what we are after is related only to energy. Such would be the case when making derivations related to temperature.
Regarding quantum mechanics, since the Hamiltonian operator will extract the energy values from the quantum states of the system, we simply count the microstates with no reference to spatial considerations if energy is the conserved quantity of interest, and thus this will amend the errors introduced by the classical approximation. Not only do quantum statisitics give the correct results (compared to the classical picture), it is sometimes easier to do the counting since the finite number of microstates comes directly from the nature of quantum mechanics and hence Gibbs tricks to force-fit classical mechanics to thermodynamics are no longer needed.
You seem to think Oleg and I are in disagreement. What he told you is correct. What I told you is correct. You are trying to do math without thinking about the physics. I don’t get the impression you understand the physics.
If you want to jump into advanced topics before you are ready, then read up on the Sackur-Tetrode equation.
Then answer the following question: In the proper calculation of the entropy of a gas contained in a box, what do you think is being counted?
Sal, this is not how microstates are counted.
In classical mechanics, states of a single particle are continuous. Counting them is akin to measuring a fluid. You need to use a measure that remains the same. For a fluid whose density can be regarded as constant, such an invariant measure is the volume, which remains unchanged if the fluid is transferred from one container into another, or even when it flows. We thus need to find a similar measure for microstates of a particle.
For simplicity, let’s work in a one-dimensional setting: the particle can only move along a line. It is not difficult to see that we cannot use the coordinate alone to define an invariant measure (what you call configurational entropy is based on that). Let’s suppose that each millimeter corresponds to, say, a million microstates of the particle. There are one million microstates between 0 and 1 mm on the x-axis, another million between 1 mm and 2 mm and so on. In your terms, h = 1,000,000 per mm. Here is how you can see that this measure does not work.
Put two particles at positions 1 mm and 2 mm at rest and let them move under an applied force. If their velocities are not the same at all times then the distance between them will shrink or expand. Instead of one particle per 1 mm we will get more or less. So this measure will not remain the same as the particles move around. We need to replace it with something more steady.
This is where phase space comes in. Picture now a two-dimensional space where one axis is coordinate x and the other is momentum p. Instead of two particles take four forming a small rectangle in this phase space. If you follow the motion of these particles, the rectangle will change its orientation and likely deform into a parallelogram, but crucially its area will not change. So says Liouville’s theorem. Now we found an invariant measure: the area in phase space. If a million particles occupy a certain area in phase space, they will continue to do so as their positions and momenta change.
So counting microstates of a single particle is done by simply measuring the volume of phase space available to it. It is the product of the three-dimensional volume in coordinate space and the volume of whatever manifold of momentum space it can access. (For example, if the particle has a well-defined energy then it would be a thin spherical shell in momentum space.) You count that volume and then divide by h to the third power. This time, h is Planck’s constant. That’s what you call Ω. Its logarithm is entropy. Note that it does not have any separate “configurational” and “thermal” parts.
For N particles in 3 spatial dimensions, the story is similar. The total number of microstates is the volume in 6N-dimensional phase space. In a microcanonical ensemble with energy E, the available phase space has no restrictions on coordinates, whereas momenta form a thin spherical shell in a 3N-dimensional momentum space. The phase space volume is, roughly, V to the power 3N times E to the power 3N/2 times some physical constants. There is no separate Ω configurational and Ω “thermal” (momentum-space, I presume) in this case. Neither is an invariant measure on its own. So entropy of an ideal gas S turns out be
plus constants independent of the volume and energy. From this one can derive various useful results, including
whence E/N = 3T/2.
The history of the Sackur-Tetrode equation is interesting because many of the paradoxes of calculating the entropy of a gas were already recognized and being addressed before quantum mechanics was developed fully. In fact, these problems come up fairly quickly in beginning courses in statistical mechanics. The history of the Sackur-Tetrode equation at least gives some assurance to alert students that they are not stupid for falling into some of those paradoxical traps.
But the entropy calculated by the Sackur-Tetrode equation goes to negative infinity as the temperature goes to zero; so this indicates that more thought about the physics needs to go into this calculation. That is a good motivator for many students.
The decades of the 1970s through to the 1990s and later produced some additional problems with the rapidly spreading meme that entropy was about disorder and everything coming all apart. The notion that entropy was all tied up in the spatial arrangements of things became so common in the public consciousness that students were bringing it into the physics classroom. Even some physics textbooks for non-majors, written by authors who should have known better, spread the meme even farther.
Apparently the chemistry textbooks for majors in chemistry picked up that meme even worse. Somewhere around the late 1990s, Frank L. Lambert of Occidental College began a campaign among the chemists to start purging this notion from the chemistry textbooks. He has had considerable success.
But it also appears the engineering and materials science textbooks picked up the meme.
I come from a generation of physicists that went through that period, and it was a battle to keep up with the meme. It was spread very effectively by aggressive marketing of creation science, and it was used most often against biology teachers, most of whom could not answer the challenge put to them by creationists who showed up in their classrooms. Duane Gish, in particular, would show up unannounced in the biology classrooms in Kalamazoo, Michigan and harass biology teachers. I knew some of those teachers. The tactic was nasty, and Gish was nasty. Those teachers labored in fear of fundamentalist creationists in the community.
I don’t know the history of that textbook by Gaskill, but I am getting the impression that some creationists may have referenced it and spread the meme “more authoritatively.” Evidently the problem continues.
If I sometimes seem cranky about ID/creationism, it is for good reason. I know their socio/political history and tactics. Students laboring under the misconceptions of the ID/creationists have an even greater handicap getting a handle on the correct science concepts in all areas of science; not just biology.
stcordova on September 1, 2012 at 3:49 pmsaid:
There is no contradiction between the classical and quantum ways of counting microstates and I disagree with your characterization of Gibbs’s results as “force-fitting” classical mechanics to thermodynamics. Classical statistical mechanics is no kludge. It is a fully consistent procedure that gives sensible results and agrees with the quantum version in the appropriate limit.
One can compare microstate counting in classical and quantum mechanics to measuring a fluid by volume and by particle number. In the limit where fluid density can be regarded as constant, either measure can be used with equal success. When we measure a fluid by volume, we don’t know exactly how many molecules it contains, and we don’t necessarily care. We just need a fair measure. Same with Gibbs’s counting. The phase-space measure, invented in the nineteenth century, provided a way to measure the “volume” of microstates. The introduction of Planck’s constant allows one to convert a phase-space volume to an actual discrete number of microstates in it. A phase-space “volume” of one Planck’s constant corresponds to one microstate.
So there is no tension between classical and quantum mechanics as far as statistical physics is concerned.
Correction to my comment above: the phase-space volume is proportional to V to the power N, not 3N, and entropy is thus
where the constant C depends on the particle number N and particle mass m. This is the Sackur-Tetrode equation that Mike mentioned. From it, you can derive all of the thermodynamics of the ideal monoatomic gas.
On Sandwalk a linked OP piece had used the ‘entropy is disorder’ soundbite, and in comments I jokingly suggested that we should sign a pledge never, ever to protray it that way again. Prof. Moran was terse (as ever): “No.”. He went on to say that this had been extensively discussed in his department, and they had not come up with a better way to portray it. I pointed him at Lambert’s website, which I think is a mine of information for the chemist – whether he looked I don’t know. He’s the Prof, I’m just a spotty graduate!
Entropy in biochemistry seems even less about order! When an exothermic reaction occurs spontaneously, but the result is a molecular bond … how is that less ordered? Of course, the energy has gone off somewhere, so we start talking of the total entropy of the system … but I’m still looking at that molecule and scratching my head!
I like Lambert’s approach of energy moving from a localised to a dispersed state. I also tend to think in terms of equilibration. Most of the matter interaction of biochemistry is following gradients – gradients of chemical potential, the electrostatic potential of binding/folding and the chemiosmotic potential generated by proton pumps. In all cases, following the gradient ‘downhill’, energy – being a conserved quantity – must be shed, and some of it is shed in all directions. It ain’t coming back.
Olegt,
Thank you very much for your detailed reply and corrections of my misunderstandings. It was very generous of you to offer so much time to this topic.
For the record, the professor who tried to teach me this over the summer did not use the distinction of Thermal and Configurational entropy, but since the term has popped up in relation to Walter Bradley’s work (and that of other materials scientists like Gaskill) I thought I would explore it. Also for the record, I was not taught entropy in terms of order and disorder, but simply in terms of the logarithm of microstates.
The professor reviewed the Liouville theorem and it was in the class text (Pathria and Beale chapter 2). My misunderstanding in this discussion are surely not his fault, or that of the class text, but the class is for engineering students with limited physics background.
I was the only one with some background in Classical Mechanics, General Relativity, and QM. The class was 12 weeks, and most (Electrical and Computer Engineers) started with no knowledge of classical thermodynamics. The final lecture was on the Bekenstein bound and Hawking radiation, the Tollman-Oppenheimer model, but he decided not to put that on our take home final since it was obviously above our heads. He just skimmed over the topics for fun.
I’m a financeer, no longer a practicing engineer, and certainly not a physicist. So thank you very much for taking time to educate the holes in my knowledge, and it will help me post on this topic in the future. As you can see, with regard to Granville Sewell, I tried to be faithful to what I learned in class. And I posted my dissent to Sewell at the risk of hurting my standing among creationists. But that’s Ok, I’m for learning and passing on accurate understanding of mainstream literature. Even if I may hold out some disagreement on some matters, it’s no excuse for not understanding what is in the mainstream.
Agreed and thank you for the correction. The way I compartmentalized in my post above was inappropriate, and I had only a guess at how Gaskill arrived at his derivation.
It would appear that Gaskill (and other material scientists) separate the portions of entropy equations that have a dependence on momentum (or energy) and call this portion “thermal” entropy, and the rest “configurational” entropy.
Adapting from Pathria and Beale for a single particle with 3 degrees of freedom
I would presume (perhaps incorrectly?) that for N particles of the same species:
Anyway, this would reduce to
which agrees with your result for an ideal gas if Boltzmann’s constant is stated in natural units of kb = 1.
It would appear Gaskill, for this case, would simply say:
and
but this is only a guess on my part, based on what I read. If so, I’d have to amend the derivation above as:
![Rendered by QuickLaTeX.com \frac{\partial S_{Conf}}{\partial E} = \frac{\partial}{\partial E} \left [ k_{B} \ln \left[V\right]^N + C \right]= 0](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%20262%2032'%3E%3C/svg%3E)
but that is a guess.
That engineering convention of
seems to cause indigestion among physicists, and for the record, that is not how I was taught it, but the convention does appear in some literature even in Universities. I do not know, off hand, if such separability is always possible in principle.
The notion is stated in Wiki as:
But the term does not appear in Pathria and Beale, and the professor never used these terms (most of his lecture material was from Fermi and Zemansky).
Anyway, using the formula:

in the context of the previous discussion of two species of gases (1 and 2) in thermal equilibrium initially separated by barrier:
After mixing

Thus for an adiabatic isothermal process for the mixing of two ideal gases of different species:
the formula I provided above, and hence entropy changes with changes in spatial configuration.
But as you said, I’m tilting at windmills with this example, since the number of microstates available to a single particle depends on the phase space of the particle which depends on the physical space available to the particle.
I’m not at all saying that entropy is about order or disorder, but I have consternation about saying entropy is only about energy with no consideration for spatial configuration.
Thank you again for the generous time you invested in helping me understand these concepts.
Sal – is Kiros Focus banned from this thread?
I see you, Sal. Can I have an answer please?
You may have surmised that I have little respect for what the ID/creationist movement has done and for the way Gish, Morris, and the rest have aggressively bullied teachers and the general public while painting their “enemies” as a defensive cabal protecting their turf.
They did a pretty good job of blindsiding the science community back in the 1970s and 80s. All that came before you knew anything about it; but those of us who were there experienced it directly. Now the ID/creationist community has to own the pile of misinformation and misrepresentations they have peddled and upon which they attempt to build their alternate reality. It’s all on the permanent record now; and the science community has an obligation to the public and to the teachers to expose it for what it is.
You have been an aggressive proselytizer of ID/creationism yourself; and I suspect you may be experiencing with your “cohorts” what I have seen many times over the years. You have just scratched the surface of that pile of misinformation and misrepresentations, and you got some pretty harsh blowback immediately. It’s up to you how you go from here.
Despite my bluntness in my replies to you, I don’t wish you any ill. I have a pretty good idea of what you are likely to encounter if you persist in scratching deeper. I don’t know what your objectives or motives are in all this, but it’s your burden and your journey; and I hope you have the honesty and strength to follow through and come out the end of it ok. Good luck to you.
If Sal has the same author privileges as any other member (no reason to think otherwise), he has quite broad permissions on any of his own threads. He cannot, however, pre-ban anyone. If KF posts a comment in one of Sal’s threads, Sal can then delete the comment and also has the option of an IP ban. (Luckily, some might say) only Lizzie has full administrator permissions, so would be able to reverse any ban though not necessarily restore a deleted comment if the author took the trouble to delete the deleted comment permanently.
In case I wasn’t clear enough, Sal can IP ban any commenter that makes a comment in a thread he has authored but that option is only available to him once a comment is posted and only in his own threads.
Rich,
Is Kairos banned from my threads? Only ceremonially in jest. Obviously the whole banning ceremony conducted at UncommonDescent (not here) was a joke. If he shows up on my threads, I’ll delete his posts, so he’s “banned” in that way. But I guess I could always unban him from my threads as long as Elizabeth still lets him through. Lighten up.
Sal
Thank you Mike. I would expect good teachers not to go easy on their students or people really trying to learn. It would be a disservice to the students to go easy on them.
I don’t know much about many things, but I will post what I learn, as I did with the 2nd law. Even after two weeks of class, and learning the Clausius postulate and Kelvin-Planck, I knew what Granville wrote couldn’t be right. I had to say something since no one on my side had said anything for years. If I didn’t say anything, it looked like no one would, and that wasn’t right.
I’m not involved in the public school debates. I don’t get in public school teacher’s faces who teach evolution. I’m not involved in school board debates, etc.
I don’t encourage creationists to avoid secular schools or get in confrontations with their professors. I encourage them to follow the example of Kurt Wise who was Stephen Gould’s student, and if they change their mind in the process of learning, that’s fine. Creationist students owe it to themselves to get the best education.
I’ve tried to be very meticulous in this thread because I wish to pass on the right information to creationists regarding the 2nd law and entropy. I will do my best to assemble the material I’ve learned in class and in these discussions and provide online essays to creationist students wishing to learn these topics. I will pass on the information you, Olegt, and my teachers have provided about the 2nd law and entorpy. I expect very few will read the essays, but I still have a responsibility to tell the truth.
Thank you also for your generous time in teaching me these topics.
Sal